Шектеулі облыстағы параболалық типтегі спектрлік-жүктелген дифференциалдық теңдеулер үшін екі шекаралық есепті шығарайық.
Кілттік сөздер: параболалық теңдеу, спектрлік, елеулі, Фурье-коэфициенті, шеттік, дифференциалдық .
Решение двух краевых задач для спектрально-нагруженных дифференциальных уравнений параболического типа в конечной области.
Ключевые слова: параболическое уравнение, спектральный, значимый, коэффициент Фурье, маргинальный, дифференциал .
Бірінші шеттік есептің берілуі.
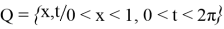
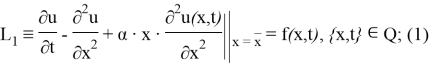
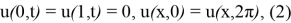
мұндағы
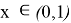
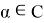
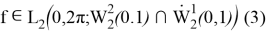
— берілген функция.
Екінші шеттік есептің берілуі.
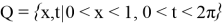
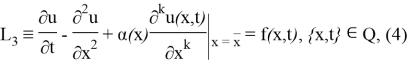
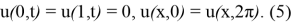
мұндағы

Ескерту 1.
(1)-(2) қатынастармен анықталатын жүктелген дифференциальдық
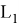
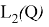
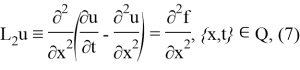
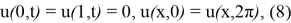
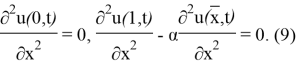
Айта кетейік, (7)-(9) шеттік есеп үшін
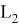
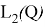
(1), (4) теңдеулері жүктелген болып табылады [1]. Берілген теңдеудің сол жағымен анықталатын оператордың негізгі бөлігінде жүктелген қосылғыштың бар болуы берілген есептің ерекшілігі болып табылады. [2,3,4] жұмыстарында негізінен осындай жүктелген операторлар қарастырылған, бірақ операторлардағы жүктелген қосылғыш әлсіз ауытқу болып табылады. (1), (4) теңдеулері үшін бұл шарт орындалмайды, сондықтан (1), (4) дифференциалдық теңдеулері спектрлік немесе «елеулі» жүктелген болып табылады.
Ескерту 2.
(4)-(5) есепті зеттеу үшін
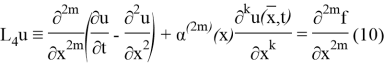
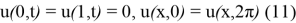
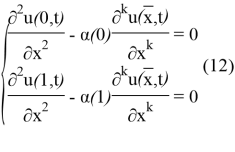
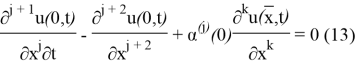
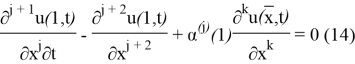
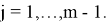
(4)-(5) және (10)-(14) шеттік есептері өзара байланысты. Шынымен де, (10)-(14) шеттік есептің регуляр шешімі (4)-(5) есебінің шешіміндей болады. Керісінше, (4)-(5) регуляр есептің шешімі талап етілген реттегі туындыларға ие болса, онда ол регуляр (10)-(14) есептің де шешімі болады.
Әрі қарай қажетті кейбір анықтамаларды береміз.
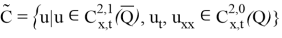
Анықтама 1.
Егер келесі шарттарды қанағаттандыратын
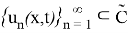
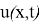
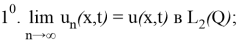
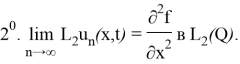
Анықтама 2. (7)-(9) шеттік есебінің әлді шешімін (1)-(2) шеттік есептің әлді шешімі деп атаймыз.
1. Әлді шешімнің жалғыз болуы мен бар болуы туралы теоремалар.
Алдымен бірінші шеттік есепті қарастырайық және ол үшін келесі тұжырымның орындалатынын көрсетейік.
Теорема 1.
Келесі шарттар орындалғанда және тек сонда ғана кез келген
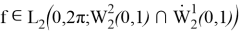
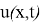
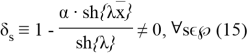
мұндағы
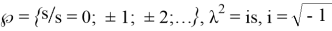
Салдар 1.
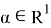
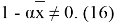
1-салдардың тұжырымдауы келесі фактінің қарапайым салдары болып табылады: кез-келген
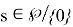
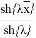
Салдар 2.
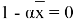
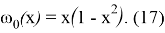
1-теореманың дәлелдеуі. Осы теореманы дәлелдеу үшін біз сызықтық шеттік есептердің әлді шешімділігін зерттеу үшін қолданылатын айнымалыларды бөліктеу әдісін дамыту бойынша А. А. Дезиннің [5] нәтижелеріне сүйенеміз.
(7)-(9) есептің шешімін келесі жіктеу түрінде іздейміз:
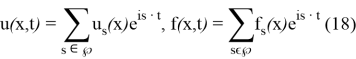
(1)-(2) шеттік есептің Фурье коэффициенттерін табу екінші ретті жүктелген, қарапайым дифференциалдық теңдеу үшін келесі шеттік есепті аламыз:
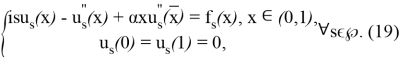
(19) есептің жалғыз шешімі келесі түрде болады:
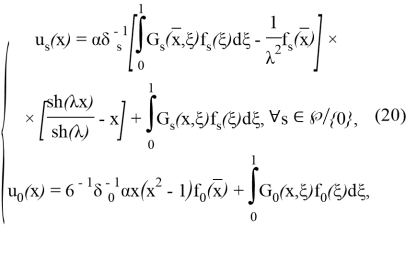
мұндағы
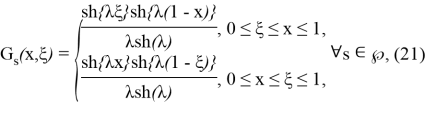
түрінде анықталады, егер
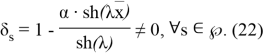
болса.
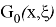
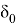
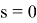
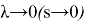
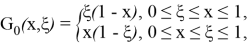
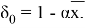
(7)-(9) есептің Фурье коэффициенттері үшін қойылған шеттік есептің регуляр шешімі
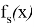
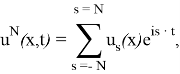
(7)-(9) шеттік есептің регуляр шешімін анықтайды, мұндағы
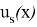
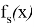
(1.1.20) формуласынан келесі априор бағалауларын аламыз:
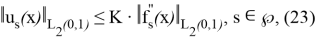
мұндағы
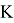
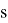
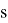
(23) бағалауын дәлелдеуде
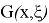
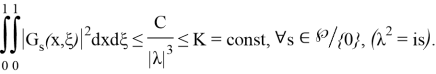
Шынымен
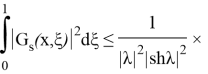
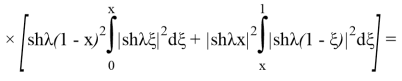
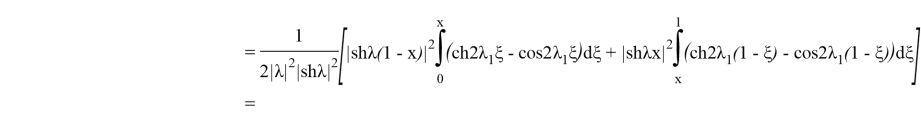
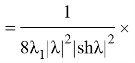
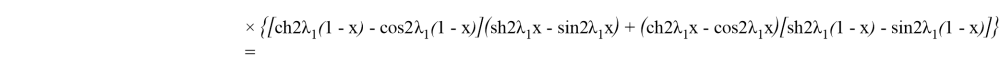
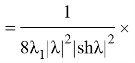
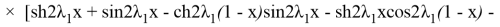
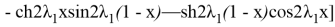
Осыдан:
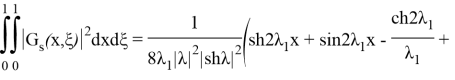
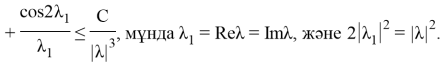
(23) бағалауды алу үшін
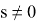
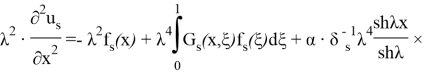
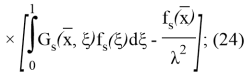
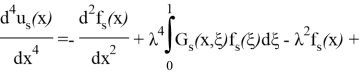
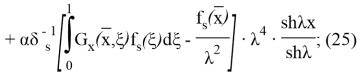
(20) формуланың жекелеген қосылғыштары мен олардың (24)- (25) туындылары үшін келесі қатынасты аламыз:
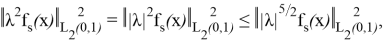
(мұнда
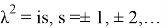
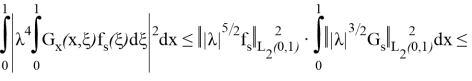
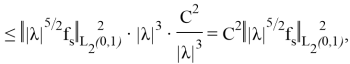
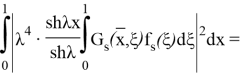
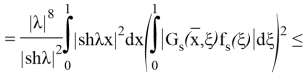
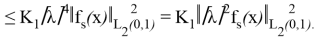
Мұнда біз келесі формуланы қолдандық:
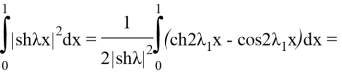
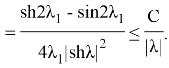
Соңғы қосылғышты бағалайық:
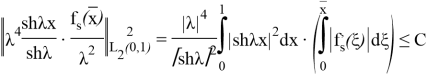
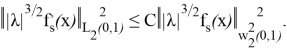
Сонымен,
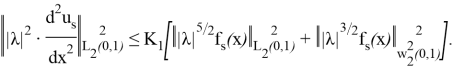
(24) теңдіктің оң жағындағы қосылғыштар (25) теңдіктің оң жағында да бар болғандықтан, келесі бағалауды алу қиын емес.
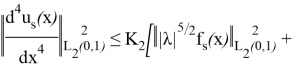
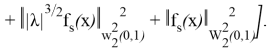
Енді (23) бағалауын алуға болады. Шынында да аламыз
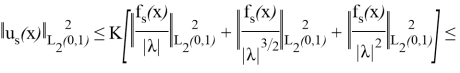
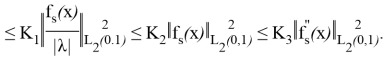
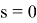
Сонымен қатар, біздің қарастырғандарымыздан
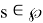
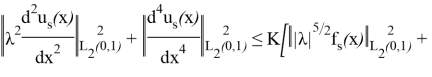
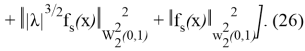
және туындылар үшін келесі бағалаулар дұрыс:
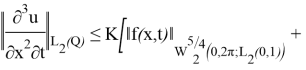
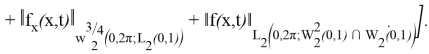
(26) және (23) бағалаулары берілген шеттік есептің әлді шешімінің дифференциалдық қасиеттерге ие болуын көрсетеді.
Дәлелдеу соңында, (3) шартында талап етілген
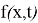
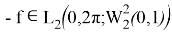
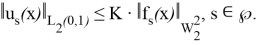
Екінші шеттік есепті қарастырайық.
Анықтама 3. Егер келесі шарттарды қанағаттандыратын
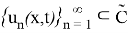
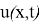
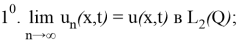
2⁰.
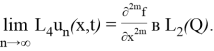
Мұнда біз
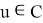
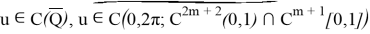
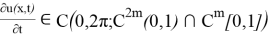
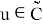
Анықтама 4. (10)-(14) шеттік есебінің әлді шешімін (4)-(5) шетті есептің әлді шешімі деп атаймыз.
Осы анықтамалардан
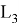
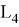
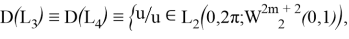
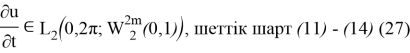
Екінші шеттік есеп үшін келесі тұжырым дұрыс болады.
Теорема 2
. Келесі шарттар орындалғанда және тек сонда ғана кез келген
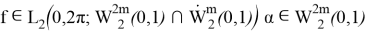
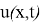
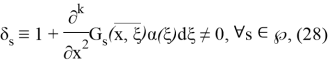
мұндағы
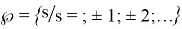
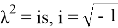
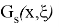
Екінші теорема бірінші теорема сияқты дәлелденеді.
Әдебиет:
- Дюво Г., Лионс Ж.-Л.Неравенства в механике и физике,М.:Наука, 1980,383с.
- Нахушев А. М. Нагруженные уравнения и их приложения// Дифференц. Уравнения, 1983, Т.19,№ 1,С.86–94.
- Дженалиев М. Т. К теории линейных краевых задач для нагруженных дифференциальных уравнений, Алматы, компьютерный центр ИТПМ,1995,270с.
- Дженалиев М. Т. О нагруженных уравнениях с периодическими граничными условиями// Дифференц. Уравнения, 2001,Т.37,№ 1,С.48–54
- Дезин А. А. Общие вопросы теории граничных задач, -М.:Наука,1980,207с







