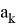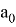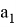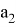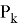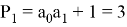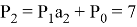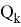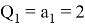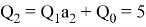Олимпиадные задачи по математике являются очень сложными и требуют глубокого понимания математических концепций и владения определенными средствами решения. Одним из мощных и гибких средств являются цепные дроби. В статье продемонстрировано, как применение цепных дробей позволяет привести более оригинальное и быстрое решение олимпиадных задач по математике.
Ключевые слова: олимпиадная задача, цепная дробь, диофантовое уравнение, иррациональное число, формула Бомбелли.
В последние годы математическое олимпиадное движение в России приобретает поистине большую популярность. Это связано с рядом факторов.
Во-первых, участие в математической олимпиаде позволяет ученикам развивать свои математические навыки и способности, а также повышать свой уровень знаний. Во-вторых, участие в таких олимпиадах позволяет школьникам сравнить свои знания со сверстниками из других регионов и стран, а также получить призы и награды за свои достижения. В-третьих, математическое олимпиадное движение предоставляет возможности для талантливых и мотивированных учеников продвигаться в своем развитии и образовании. И, наконец, математические олимпиады в России получили признание как средство выявления и поддержки математического потенциала учащихся. Многие университеты и международные организации учитывают результаты олимпиад при приеме на обучение или при присуждении стипендий и грантов [2].
Олимпиады ставят целью выявить и поддержать талантливую молодежь и поэтому задания для таких мероприятий подбираются таким образом, чтобы отобрать сильнейших участников. Как правило, такие задания имеют нестандартный характер, требуют нетривиального подхода к решению, проявления логического мышления и творческих способностей [4].
В данной работе рассмотрим, как использование цепных дробей позволяет привести более быстрое и оригинальное решение олимпиадных задач по математике.
Цепные дроби имеют широкое применение в олимпиадных математических задачах. Они могут быть использованы для решения уравнений или систем уравнений, а также для исследования свойств чисел. Рассмотрим следующую задачу.
Задание 1 . (Олимпиадная задача по математике из коллекции задач «Турнира Ломоносова» Г. А. Гальперин. 7, 8, 9 классы). Решите уравнение в целых положительных числах.
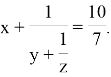
Решение . Представим в виде цепной дроби число
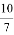
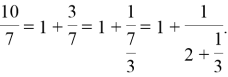
Поскольку всякое рациональное число можно представить в виде конечной цепной дроби и притом единственным образом, то очевидно, что
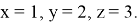
Уравнение из первой задачи называется диофантовым. Главная трудность, с которой сталкиваются ученики при решении таких уравнений, состоит в том, чтобы найти какое-нибудь его частное целочисленное решение. Рассмотрим задачу, в решении которой цепные дроби позволяют довольно несложно это сделать.
Задача 2. (Олимпиада для школьников «Малый мехмат» МГУ им. В. М. Ломоносова). В некотором тридесятом царстве государь установил, что купюры могут быть только номиналом 17 и 12 рублей. Один из жителей хочет приобрести на рынке яблоко за 1 рубль. Принимая во внимание, что как у продавца, так и у покупателя есть сколь угодно много купюр соответствующего номинала, то каким образом покупатель должен расплатиться за приобретаемый товар?
Решение
. Пусть
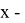
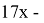
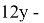
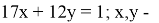
Для решения данного уравнения применим теорию цепных дробей.
Представим число
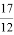
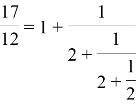
Далее определим значения чисел
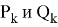
Таблица 1
Вычисление значений
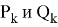
|
|
|
|
|
|
|
1 |
2 |
2 |
||
|
|
1 |
1 |
|
|
|
|
0 |
1 |
|
|
Тогда
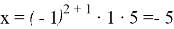
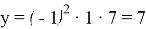
Таким образом, чтобы приобрести яблоко, покупатель должен передать 5 купюр номиналом в 117 рублей продавцу, который, в свою очередь, выдаст сдачу в размере 7 купюр номиналом 12 рублей.
Кроме того, цепные дроби могут быть использованы для исследования свойств чисел, например, для представления иррационального числа. Рафаэль Бомбелли пришёл к цепным дробям, изучая извлечение квадратного корня из чисел. Первым известным использованием непрерывной дроби является приближённое выражение для
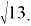
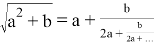
Задача 3. (Олимпиада школьников «Ломоносов-2008». Заключительный этап. 10–11 классы). Найти 𝑘, если
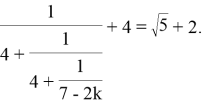
Решение :
Преобразуем равенство, чтобы в правой его части остался только
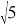
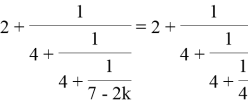
Тогда
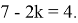
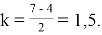
Наконец, теория цепных дробей позволяет находить значения числовых выражений. Так, при исследовании периода десятичной дроби, цепные дроби могут помочь в поиске закономерностей в последовательности цифр. Рассмотрим следующую задачу.
Задача 4 . (Международная олимпиада по математике «Турнир городов», Г. А. Гальперин). Найдите значение выражения
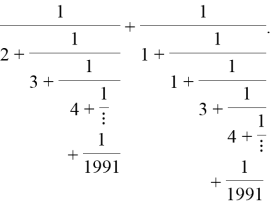
Решение
. Заметим, что в каждом из слагаемых содержится одинаковая часть выражения. Заменим ее на
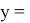
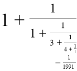
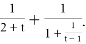
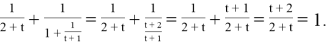
Таким образом, цепные дроби являются мощным инструментом для анализа чисел и решения олимпиадных математических задач. Их использование требует хорошего понимания свойств цепных дробей и навыков их применения. Решения представленных задач продемонстрировали как с помощью данного инструмента без особых усилий можно добиться качественных результатов.
Литература:
- Арнольд В. И. Цепные дроби квадратных корней из рациональных чисел и их статистика / В. И. Арнольд // Успехи математических наук. 2007. — Т. 62. — № 5 (377). — С. 3–14.
- Боташева З. Х., Аманова Б. А. Олимпиадные задачи по математике как средство развития творческого мышления студентов / З. Х. Боташева, Б. А. Аманова // Педагогическое мастерство и современные педагогические технологии. Сборник материалов III Международной научно-практической конференции. — Чебоксары: Общество с ограниченной ответственностью «Центр научного сотрудничества «Интерактив плюс», 2017. — С. 35–38.
- Смолин Ю. Н. Алгебра и теория чисел: учеб. пособие для студ. Физ.-мат. фак. высших пед. учеб. заведений / Ю. Н. Смолин. — 3-е изд., испр. — М.: Флинта: Наука, 2006. — 463 с.
- Сухова, К. И. Цепные дроби как средство обучения решению олимпиадных задач по математике / К. И. Сухова, М. В. Глебова // Современные тенденции развития системы образования: материалы Междунар. науч.-практ. конф. (г. Чебоксары, 25–28 апреля 2019 г.). — Чебоксары: Среда, 2019. — С. 205–208.