В данной статье автор рассматривает особую геометрическую фигуру — треугольник Рёло. В частности, описывает процесс построения данной фигуры и рассматривает её свойства. Так же, автор приводит примеры применения свойств треугольника Рёло в повседневной жизни.
История появления
Треугольник Рёло — это область пересечения трех окружностей, построенных из вершин правильного треугольника. Они имеют радиус, равный стороне этого же треугольника. Он относится к разряду простых фигур, обладающих постоянной шириной, то есть если к нему провести две параллельные опорные прямые, то независимо от выбранного направления, расстояние между ними будет неизменным, в любой точке независимо от их длины.
Название это необычной фигуре дал немецкий механик Франц Рёло. Историки утверждают, что именно он стал первым, кто обнаружил свойства этой фигуры. Но Рёло был не первым, кто обнаружил эту фигуру. Иные исследователи первооткрывателем этой фигуры называют Леонарда Эйлера, который жил 100 лет назад.
Существуют более ранние упоминания об этом треугольнике. Такая фигура встречается раньше, в XV веке: её использовал Леонардо да Винчи (рис. 0).

Рис. 1
Построение
Рассмотрим равносторонний треугольник ABC . Пусть у этого треугольника сторона равна r . Тогда построим окружность с центром в точке А и радиусом r . Назовём эту окружность w 1 . Заметим, что эта окружность проходит через вершин В и С . Дальше аналогично построим окружности w 2 и w 3 с центром в вершинах В и С . И заметим, что меньшая дуга BC окружности w 1 , меньшая дуга АС окружности w 2 и меньшая дуга AB окружности w 3 образуют сам треугольник Рёло. (рис. 2)
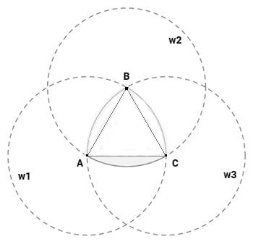
Рис. 2
Также существует иной способ построения. Нарисуем окружность q 1 с центром O 1 . Выберем любою точку O2 , которая лежит на окружности. Затем, с центром в этой точке точки построим окружность q 2 , с тем же радиусом, что и радиус окружности q 1 . Дальше заметим, что есть две точки пересечения окружностей q 1 и q 2 . Выберем одну из них и назовём её O3 . И проведём с центром уже в этой точке окружность q 3 , радиус которой будет равен q 1 . И заметим, что фигура, которая образована пересечением сразу всех трёх окружностей, будет являться искомым треугольником Рёло. Заметим, что точки O 1 , O 2 и O 3 действительно образуют равносторонний треугольник, так как по построению: O 1 O 2 — радиус q 1 = радиусу q 2 — O 2 O 3 . И так как O 3 лежит и на q 2 , и на q 1 , то и O 1 O 2 = O 1 O 3 . Отсюда O1O2 = O2O3 = O3O1 .
Основные свойства
В дальнейшем, все действие будут производиться, основываясь на чертеже, который изображён на рис. 1
Давайте определим площадь и периметр полученного треугольника Рёло.
Начнём с площади. Заметим, что площадь треугольника АВС равна по формуле

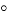

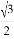
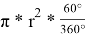
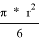
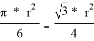
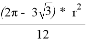
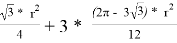
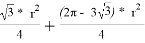
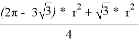
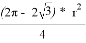
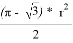

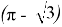
Далее определим периметр треугольника Рёло. Заметим, что он состоит трёх равных отрезков дуг, так как они заключены между равными углами. Тогда обозначим L — длину этого отрезка дуги, тогда 3L — периметр нашего треугольника Рёло. L в свою очередь равно
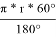
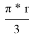
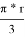
ПРИМЕНЕНИЕ И РАСПРОСТРАНЕНИЕ ЖИЗНИ
Можно подумать, что треугольник Рёло не особо распространён в жизни, однако его можно заметить на различных зданиях архитектуры или в различных приспособлениях. Например, окно в форме треугольника Рёло можно обнаружить в церкви Богоматери в бельгийском городе Брюгге и швейцарском Гаутериф (рис. 3).

Рис. 3
Также, свойства треугольника Рёло использовали немецкие инженеры Вальтер Фройде и Феликс Ванкель, когда разрабатывали роторно-поршневой двигатель (рис. 4), который имеет очень высокую удельную мощность и гораздо меньшие габариты по сравнению с другими двигателями. Такой двигатель используется на некоторых самолётах, но в основном в машинах — на первых порах, такой двигатель использовался японской фирмой Mazda и советской фирмой ВАЗ. В нынешнее время, устранив недостатки ранних версий, в основном использует для своих автомобилей фирма Mazda.

Рис. 4
И ещё один яркий пример использования треугольника Рёло — дизайн. Знаки, обозначающие исторические маршруты в США, выполнены в форме треугольника Рёло (рис. 5), центральная кнопка одной из версий телефона компании Samsung тоже выполнена в его форме (рис. 6). Даже медиаторы сделаны в форме треугольника Рёло (рис. 7).

Рис. 5

Рис. 6

Рис. 7.










