Задания второй части ОГЭ направлены на проверку владения материалом на повышенном уровне. В своей статье автор рассматривает основные идеи для решения геометрической задачи № 25 ОГЭ по математике. При подготовке к экзамену по математике большинство задач по планиметрии не решается с помощью строгих алгоритмов, почти каждая геометрическая задача требует своего подхода. Задача 25 требует свободного владения материалом и достаточно высокого уровня математического развития, рассчитана на обучающихся, изучавших математику углубленного уровня. Требования к выполнению заданий с развернутым ответом заключаются в следующем: решение должно быть математически грамотным и полным, из него должен быть понятен ход рассуждений. Оформление решения должно обеспечивать выполнение указанных выше требований, а в остальном может быть произвольным.
Для решения геометрических задач применяются три основных метода: геометрический, алгебраический, комбинированный.
Геометрический метод
Основная идея геометрического метода состоит в том, что задача решается чисто геометрическим способом, т. е. все рассуждения строятся на применении известных аксиом, утверждений, теорем.
Алгебраический метод
Данный метод основан на применении основных алгебраических структур, таких как, уравнения, системы уравнений. При решении задач таким методом геометрические элементы находят с помощью составления взаимосвязей между ними и решения уравнений.
Комбинированный метод
Часто задачи по геометрии решаются комбинированным методом. В данном методе сочетаются геометрический и алгебраический способы решения геометрических задач. С помощью логических рассуждений, использующих основные геометрические теоремы и утверждения, решается часть задачи, доказываются необходимые моменты для дальнейшего решения задачи алгебраическим методом.
Основные этапы решения геометрических задач
При решении геометрических задач необходимо придерживаться следующего плана действий, чтобы прийти к ожидаемому результату:
- Чтение условия задачи.
- Выполнение чертежа.
- Краткая запись условия задачи (дано, найти).
- Перенос данных условий на чертёж, выделение элементов чертежа различными цветами.
- Анализ данных задачи (поиск решений).
- Составление алгоритма решения.
- Запись решения.
- Проверка соответствия найденных элементов условию задачи.
- Запись ответа.
Для решения задач № 25 нужны соответствующие умения:
- Нужно знать признаки, свойства и теоремы, связанные со всеми геометрическими фигурами.
- Во многих случаях решать задачи помогает введение в чертеж дополнительных линий — так называемые дополнительные построения. Такие дополнительные построения, вводящие новые углы и новые отрезки, иногда приводят к появлению геометрических фигур, облегчающих решение задачи.
- Знать свойства элементов геометрических фигур
- Уметь правильно доказывать свойства геометрических фигур
Частые ошибки при решении этой задачи:
- Ошибки при выполнении чертежа, например, изображение трапеции вместо параллелограмма
- Применение свойств несуществующей средней линии параллелограмма;
- Путают признаки равенства треугольников с признаками подобия треугольников
- Используют не существующие признаки равенства треугольников по трем углам, либо признак формулируют неверно.
Основные типы заданий № 25 в ОГЭ:
– задачи, связанные с треугольниками;
– задачи, связанные с четырехугольниками;
– задачи на применение умений работать с окружностями;
– задачи на комбинацию многоугольников и окружностей.
Рассмотрим несколько примеров экзаменационных задач № 25
Треугольники
-
В остроугольном треугольнике АВС проведены высоты АК и СМ. Из точки М на сторону ВС опущен перпендикуляр МЕ, а из точки К на сторону АВ опущен перпендикуляр КН. Найдите
Решение:
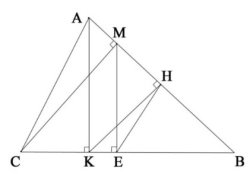
1) Рассмотрим прямоугольные треугольники АКВ и СМВ. Они подобны, так как имеют прямой угол и общий угол В. Следовательно,

2) Рассмотрим прямоугольные треугольники МЕВ и КНВ. Они тоже подобны, так как имеют прямой угол и общий угол В. Следовательно,

3) Из пунктов 1 и 2 получаем, что
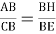
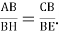
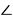
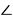

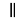
Ответ: 68°.
Четырехугольники
- В параллелограмме АВСD биссектрисы углов А и В пересекаются в точке К. Сторона ВС параллелограмма равна 4, высота КН треугольника АВК равна 3. Найдите площадь параллелограмма АВСD.
Решение.
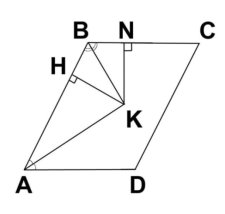
1) Проведём перпендикуляр КN к прямой ВС.
2)
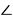
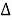
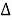
3) Таким образом, НК = NК = 3.
4) Аналогичным образом проведем перпендикуляр из точки K к прямой АD и получим, что расстояние от К до АD равно 3.
5) Следовательно, высота параллелограмма равна 3 + 3 = 6, откуда SABCD = 6

Ответ: SABCD = 24.
Окружности
-
Окружность радиуса R касается луча QР в точке Р и пересекает луч QС в точках D и С (QD < QC). Известно, что РD =

Решение.

1) Квадрат касательной равен произведению секущей на ее внешнюю часть:


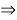
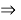
2) По теореме косинусов для треугольника QРD получаем:
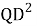

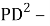


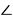
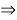
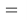
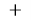


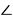
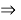
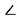

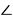
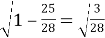
3) Угол между касательной и хордой равен половине дуги, отсекаемой этой хордой, т. е. равен вписанному углу, опирающемуся на эту хорду. Значит,
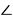

4) По теореме синусов для треугольника РDС получаем:

Ответ:

Комбинация многоугольника и окружности
- Четырехугольник АВСD со сторонами АВ = 12 и СD = 30 вписан в окружность. Диагонали АС и ВD пересекаются в точке К, причем АКВ = 60°. Найдите радиус окружности, описанной около этого четырехугольника.
Решение.
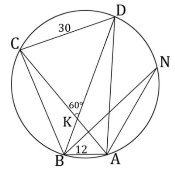
1) Построим хорду АN = СD = 30. Рассмотрим треугольники КАD и АВN.
Они подобны по двум углам:
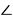
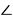
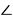
2) Тогда
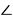
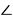
3) По теореме косинусов в треугольнике ANB:
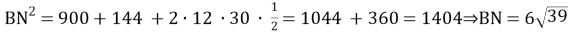
4)
По теореме синусов в треугольнике ANB:
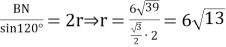
Ответ: 6
Литература:
- Я. П. Понарин. Элементарная геометрия. Том 1/МЦНМО. — 2018
- К. В. Башашина О. Н., Курченко, Ю. И. Попов. Практикум по решению планиметрических задач: учебное пособие/ — Калининград. — 2015
- Образовательный электронный портал РЕШУ ОГЭ/СДАМ ГИА









