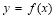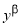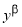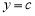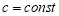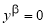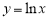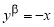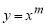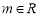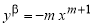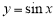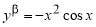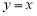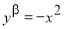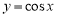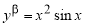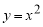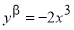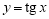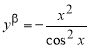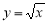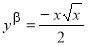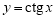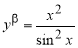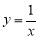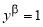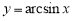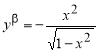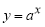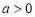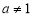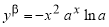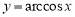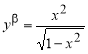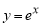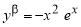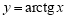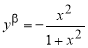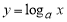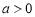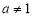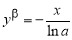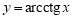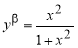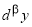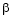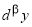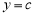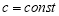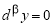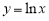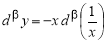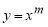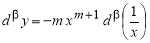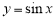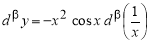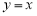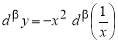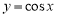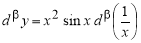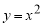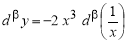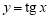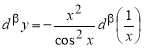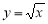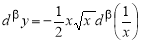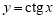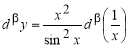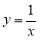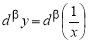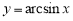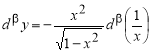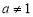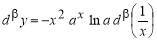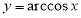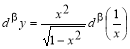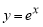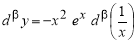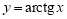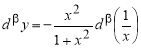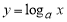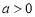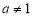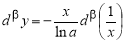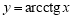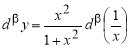Мир производной и дифференциала. Необычное в привычном



Рассмотрено обобщение понятий производной и дифференциала функции. Определены β-производная и β-дифференциал. Составлены таблицы β-производной и β-дифференциала основных элементарных функций. Выяснен их геометрический смысл. Рассмотрено применение β-дифференциала в приближенных вычислениях. Приведены примеры.

Ключевые слова: β-производная, β-дифференциал, геометрический смысл, приближенные вычисления функции.

Введение

Производная и дифференциал являются основополагающими понятиями дифференциального исчисления — раздела математического анализа. Эти понятия тесно связаны друг с другом.

Настоящая работа представляет собой изложение исследований, связанных с обобщениями производной и дифференциала функции, которые мы называем β-производной и β-дифференциалом. Они определяются аналогично обычной производной и обычному дифференциалу. Исследование посвящено неклассическому дифференциальному исчислению. Целью работы является разработка некоторых основных положений его модификации.

Объект исследования —β-производная и β-дифференциал. Предмет исследования — свойства β-производной и β-дифференциала функции. Достижение поставленной цели связано с решением нижеследующих задач :

1) определить понятия β-производной и β-дифференциала, ввести их обозначения;

2) составить таблицы β - производных и β - дифференциалов;

3) записать уравнения касательной и нормали к графику функции в данной точке с помощью β - производной;

4) установить формулу, выражающую зависимость между β - производной и обычной производной;

5) выяснить геометрический смысл β - производной (β - дифференциала);

6) рассмотреть применение β - дифференциала в приближенных вычислениях и оценить, насколько целесообразно использование β - дифференциала в приближенных вычислениях.

Можно привести достаточно много различных обобщений производной и дифференциала. Исследование их представляет несомненный интерес в связи с выявлением новых сведений и фактов, которые могут сделать теорию дифференциального исчисления более развитой, богатой и разнообразной. Исходя из этого, стоит отметить, что предлагаемое исследование имеет некоторую неклассическую параллель с работой [1]. На основании вышеизложенного следует актуальность выбранной темы данной работы. Основными методами исследования , применяемыми в работе, являются методы классического дифференциального исчисления.

Основная часть

Определение 1. Пусть функция определена на промежутке и — внутренняя точка этого промежутка; β -производной заданной функции в точке (будем обозначать: ) назовем следующий предел

(1)

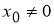
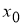
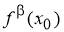
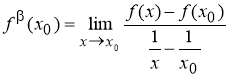
(если этот предел существует).

Функцию, имеющую конечную β-производную в некоторой точке, будем называть -дифференцируемой в данной точке. Нахождение β-производной функции назовем - дифференцированием этой функции.

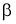
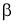
Пример 1. Запишем формулу для нахождения -производной степенной функции

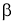
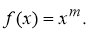
Решение . Учитывая формулу (1) и первое правило Лопиталя [2], получаем:

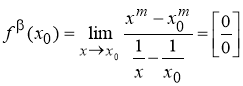
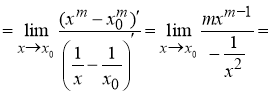
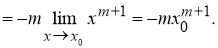
Следовательно, , т. е.

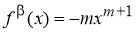
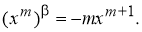
Аналогично находим β-производные остальных основных элементарных функций. Сведем эти формулы в таблицу 1.

Таблица 1. β- Производные основных элементарных функций

Функция	β - Производная	Функция	β - Производная
,
,
, ,
, ,

Пример 2. Запишем уравнения касательной и нормали к графику функции в точке используя -производную.

Решение. Уравнение касательной к графику функции в точке имеет вид:

, (2)

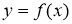
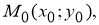
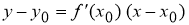
где — значение обычной производной этой функции в заданной точке [2].

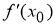
Выразим через :

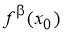
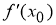
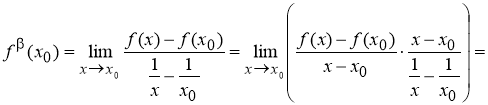
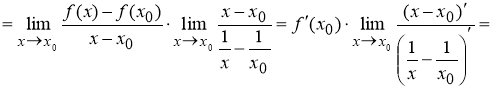
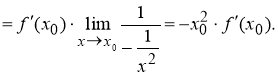
Таким образом, . Отсюда Подставляя найденное выражение для в уравнение (2), получаем искомое уравнение касательной:

(3)

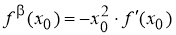
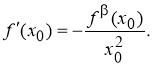
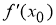
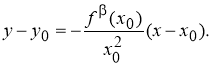
Используя уравнение нормали к графику функции

в точке [2]:

,

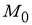
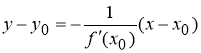
запишем искомое уравнение нормали:

.

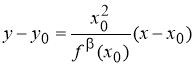
Теорема 1 (геометрический смысл -производной). Пусть имеем семейство гиперболических кривых вида , проходящих через точку , и выделим ту из них, которая имеет наилучшую степень приближения к кривой

в окрестности точки (рис.1). Тогда имеет место равенство :

. (4)

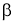
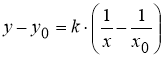
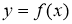
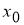
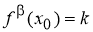
Доказательство. Если гиперболическая кривая , проходящая через точку , имеет наилучшую степень приближения к кривой в окрестности точки , то эти обе кривые имеют общую касательную в этой точке.

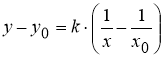
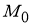
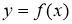
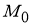
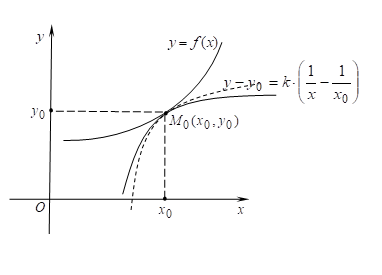
Рис. 1

Запишем уравнение касательной к рассматриваемой кривой в точке :

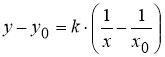
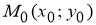
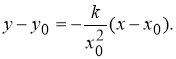
Принимая во внимание уравнение (3) касательной к кривой в точке , приравняем угловые коэффициенты этих касательных: Отсюда следует равенство (4).

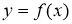
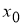
Теорема доказана.

Определение 2. Если приращение функции можно представить в виде

(5)

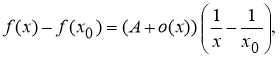
где – бесконечно малая величина при , то данную функцию будем называть -дифференцируемой в точке , а выражение — - дифференциалом функции в точке

и будем обозначать: (или

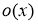
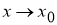
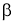
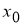
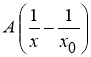
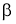
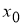
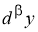
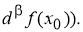
Пример 3. Используя - дифференциал, вычислим приближенно (с точностью до тысячных).

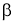
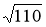
Решение . Пользуясь таблицей 1, запишем . Таким образом, получаем формулу для приближенного вычисления:

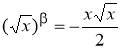
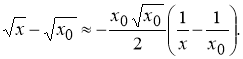
Отсюда находим

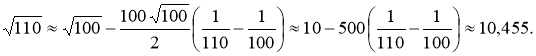
Для сравнения приведем точное значение корня с четырьмя знаками после запятой:

.

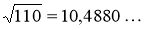
Ответ : 10,455.

Приведенный пример показывает, что рассматриваемое обобщение дифференциала может быть полезным в приближенных вычислениях.

Теорема 2. Справедлива следующая формула

. (6)

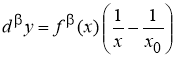
Доказательство. Из формулы (5) получаем:

Тогда

= .

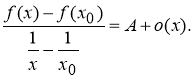
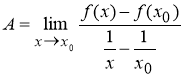
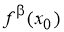
Учитывая определение 2, имеем: . Следовательно,

,

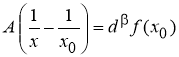
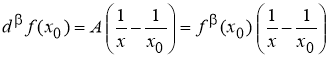
отсюда вытекает формула (6).

Теорема доказана.

Замечание. Сучетом равенства:

, запишем формулу

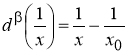
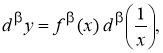
равносильную формуле (6).

Формулы -дифференциалов основных элементарных функций приведены в таблице 2.

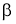
Таблица 2

β- Дифференциалы основных элементарных функций

Функция	β - Дифференциал	Функция	- Дифференциал
,
,
, ,
, ,

Теорема 3 (геометрический смысл -дифференциала). β- Дифференциал функции

в точке равен приращению ординаты этой точки на кривой

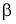
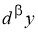
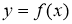
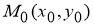
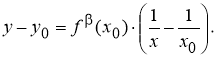
Доказательство. Рассмотрим график функции (рис.2), пусть точка принадлежит этому графику. Кроме того, рассмотрим гиперболическую кривую вида , которая имеет наилучшую степень приближения к кривой в окрестности точки .

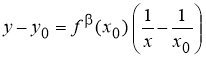
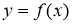
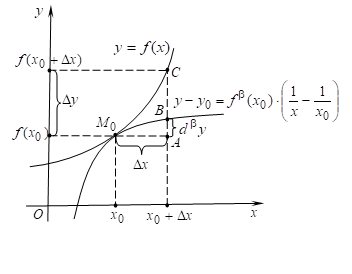
Рис. 2

Если абсциссе придать приращение , то ордината точки на кривой получит приращение А ордината соответствующей точки на логарифмической кривой получит приращение , причем

.

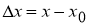
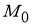
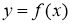
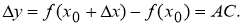
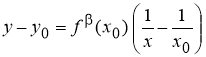
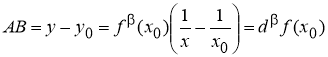
Теорема доказана.

Заключение

Установлены некоторые основные положения нового направления неклассического дифференциального исчисления. Цель данной работы достигнута, а также решены задачи, сформулированные во введении. Полученные результаты сопровождаются комментариями и иллюстрируются примерами. Результаты работы являются новыми, получены авторами самостоятельно, имеют теоретическую и практическую значимость. Работа может быть использована для проведения дальнейших исследований. Исследование может быть полезно и интересно всем, кто интересуется математикой. Очень интересно и познавательно — видеть знакомое в незнакомом! Необычное в привычном ….

Литература:

1. Анисимова Е. Э. Взгляд на производную и дифференциал с другого ракурса / Е. Э. Анисимова, А. И. Илларионова, А. З. Пчелова // Национальное достояние. 2020, № 3(4). С. 40–49.
2. Задачи по математике. Начала анализа / В. В. Вавилов, И. И. Мельников, С. Н. Олехник, П. И. Пасиченко. М.: Физматлит, 2008. 284 с. (Библиотека учителя математики и школьника).