Обслуживание систем со стратегией последовательных восстановлений после отказов
Авторы: Дагаев Александр Владимирович, Сорокин Алексей Андреевич
Рубрика: 1. Информатика и кибернетика
Опубликовано в
Дата публикации: 02.07.2020
Статья просмотрена: 118 раз
Библиографическое описание:
Дагаев, А. В. Обслуживание систем со стратегией последовательных восстановлений после отказов / А. В. Дагаев, А. А. Сорокин. — Текст : непосредственный // Технические науки: проблемы и перспективы : материалы VII Междунар. науч. конф. (г. Казань, июль 2020 г.). — Казань : Молодой ученый, 2020. — С. 1-13. — URL: https://moluch.ru/conf/tech/archive/377/15972/ (дата обращения: 04.05.2024).
В статье рассмотрен вопрос моделирование стратегий функционирования. Приведены требования к моделированию данных стратегий. Кратко изложена основная последовательность действий при моделировании. Приведен пример построения программы, реализующей данную последовательность. Сделан общий вывод по возможностям применения конечного результат.
Ключевые слова: обслуживание систем, стратегии функционирования, коэффициент готовности, отказ, восстановление.
Развитие информационных технологий приводит к возможности моделировать работу любых систем. Это относится к высоконадежному оборудованию, которое используется во сферах деятельности, энергетическим установкам, авиационной и космической технике. Моделирование позволяет анализировать характеристики систем. Имитация может быть использована и для моделирования систем с различными стратегиями обслуживания. Основная задача данной статьи — показать общие этапы проектирования системы для моделирования элементов со стратегиями отказа и восстановления.
Описание стратегии функционирования
Модель учитывает наличие встроенного контроля с мгновенной фиксацией отказов в системе и ее полное восстановление в случае отказа. Контроль работоспособности осуществляется в системе постоянно. В случае отказа система останавливается и находится в неработоспособном состоянии до момента восстановления. Рассмотрим стратегию функционирования более подробно.
Считается, что в начальный момент времени
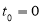
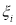
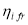
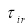

Рис. 1. Стратегия системы со встроенным контролем
Рассмотрим обозначения, используемые в этой модели: ‘+’ и ‘-‘ характеризуют рабочее и нерабочее состояние системы;
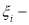
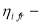
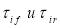
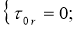
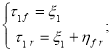
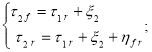
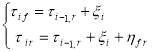
Опишем состояние системы с представленной стратегией обслуживания в случайный момент процессом
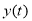
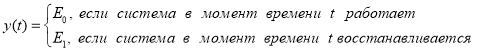
Диаграмма переходов процесса
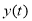
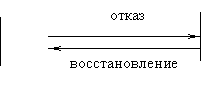
Рис. 2. Диаграмма переходов процесса
Описание процесса моделирования
Для моделирования времени отказа и восстановления использовались случайные величины, распределенные по нормальному закону и экспоненциальному закону. При моделировании случайных величин использовалось преобразование Бокса — Мюллера. Данный метод позволяет моделировать стандартные нормально распределенные величины. Метод является точным, в отличие, например, от методов, основывающихся на центральной предельной теореме. Метод имеет два варианта реализации. Нами был выбран второй вариант данного преобразования, который позволяет получить пару независимых нормально распределенных случайных величин с математическим ожиданием 0 и дисперсией 1 следующим образом:
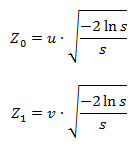
где
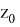
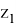
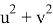
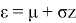
где
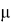
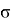
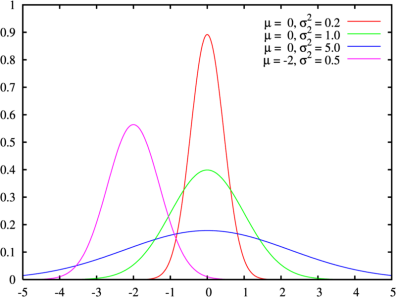
Рис. 3. Пример плотности нормального распределения
Сравним его с табличным методом генерации нормально распределенных чисел. Данный метод состоит из того, что: нормальное число можно взять из справочника в таблице функции Лапласа и получить случайное число по методу взятия обратной функции: x = F–1(r), где F — интегральная функция Лапласа. Технически это означает, что надо разыграть случайное равномерно распределенное число r из интервала [0; 1] стандартным ГСЧ, найти равное ему число в таблице значений функции Лапласа в столбце F и по строке определить случайную величину x, соответствующую этому числу. Недостатком метода является необходимость хранения в памяти компьютера всей таблицы чисел функции Лапласа. Поэтому преобразование Мюллера будет менее затратным, а скорость будет выше.
Далее представим моделирование экспоненциального распределения с помощью метода обратной функции. Функция плотности f(t) экспоненциального распределения случайной величины и функция распределения F(t) задаются формулами:
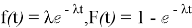
где
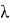
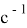
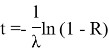
Известно, что функция случайной величины R имеет такое же распределение, что и сама случайная величина R. Поэтому формулу выше представим в виде:
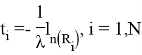
Сложность данного алгоритма O(N). [1]
Пример плотности экспоненциального распределения (см. рис. 4).
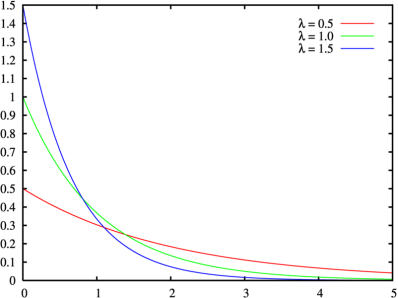
Рис. 4. Пример плотности экспоненциального распределения
Сравним его с методом кусочной аппроксимации. Данный метод состоит из того, что: выбрать вероятности попадания во все интервалы
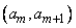
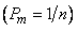
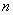
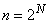
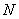
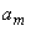
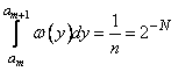
При равенстве вероятностей
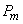
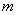
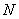
Из датчика равномерно распределенных в интервале (0, 1) случайных чисел извлекается пара реализаций
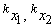
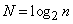
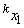
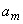
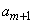
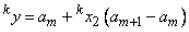
получается реализация
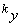
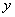
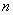
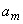
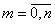
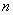
Расчет коэффициента готовности
Коэффициент готовности — это вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени, кроме планируемых периодов, в течение которых применение объекта по назначению не предусматривается. Формула расчета неасимптотического коэффициента готовности системы с текущей стратегией обслуживания записывается в следующем виде:
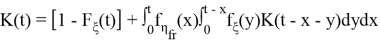
Асимптотический коэффициент готовности для представленной стратегии представлен в формуле 2.
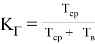
где
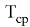
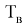
Пример расчета
Возьмем исходные данные такие: за отказ — экспоненциальное распределение, для восстановления — нормальное распределение. За математическое ожидание возьмем значение равное 100 часов, за среднеквадратичное отклонение возьмем значение равное 10 часов, за лямбду возьмем значение равное 1 часу, за время моделирования возьмем 10000 часов, а количество итераций равным 100000.
Шаг 1 . Сначала происходит моделирование отказа — восстановления. Отказ моделируется экспоненциальным распределением с помощью метода обратной функции, восстановление моделируется нормальным распределением с помощью преобразования Бокса-Мюллера. Данное моделирование происходит для 100000 итераций в течении 10000 часов для каждой итерации с шагом в 1 час (т. е. происходит сбор статистики). Для всех 100000 итераций создается один список.
Шаг 2 . Считывается состояния и времена из списка states, а после происходит подсчет среднего времени восстановления и среднего времени отказа, то есть суммируется время до первого отказа и суммируется время самого отказа соответственно, а после рассчитывается коэффициент готовности по формуле 1. Результаты коэффициента готовности записываются в специальный список. Далее рассчитывается один из коэффициентов готовности по формуле 1 в любой момент времени t, к примеру, среднее время между отказами равно 150, а среднее время до восстановления 120 часов:
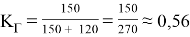
Шаг 3 . Далее считываются результаты и происходит построение графика. График строится в соотношении [время; коэффициент готовности] (см. рис. 5).
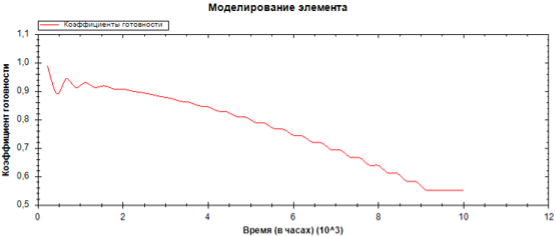
Рис. 5. Пример построенного графика
Шаг 4 . Далее результаты моделирования экспортируются для дальнейшей обработки.
Результаты моделирования
Для апробации был разработан программный продукт (рис. 6) с экспортом данных файл электронных таблиц. При тестировании в качестве времени отказа было взято экспоненциальное распределение, для времени восстановления — нормальное распределение. Математическое ожидание было принято равное 100 часов, за среднеквадратичное отклонение возьмем значение равное 10 часов, обратную величину к интенсивности отказов (Тср) возьмем равным 1 часу. Время моделирования примем равным 10000 часам, а количество итераций равным 100000. В ходе проведенных расчетов были получены результаты представленные на рис. 5–8.
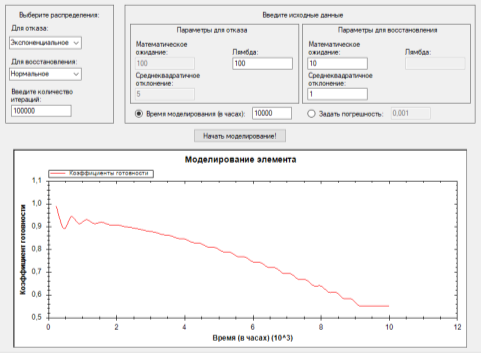
Рис. 6. Результат моделирования
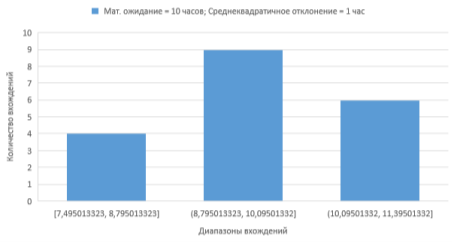
Рис. 7. Нормальное распределение
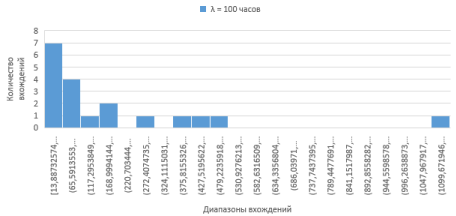
Рис. 8. Экспоненциальное распределение
Таким образом, видно, что при длительной работе системы, ее неасимптотический коэффициент готовности стремится к асимптотическому коэффициенту, который примерно равен 0,553.
Приведем пример с нормальным законом распределения времени отказа. Математическое ожидание времени отказа возьмем равным 100 часам, среднеквадратичное отклонение возьмем равным 5 часов. Математическое ожидание для восстановления возьмем равным 5 часов, среднеквадратичное отклонение возьмем значение равное 1 часу, время моделирования возьмем равным 10000 часам, а количество итераций примем 100000. В результате расчетов был получен график представленный на рис.9.
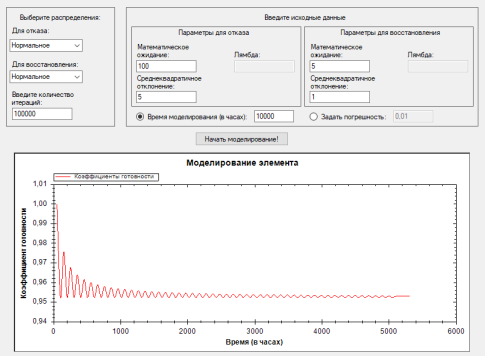
Рис. 9. Моделирование с нормальным распределением времени отказа и восстановления
Таким образом, асимптотика началась после 5000 часов, асимптотический коэффициент готовности равен примерно 0,952. Хотя на практике восстановление редко может носить экспоненциальный характер, но теоретически это возможно. Рассмотрим вариант с экспоненциальным распределением времени отказа и восстановления. Среднее время до отказа возьмем 100 часов. Среднее время восстановления возьмем значение 10 часов, время моделирования примем 100000 часов, а количество итераций равным 100000. В результате были получены результаты моделирования представленные на рис.10.
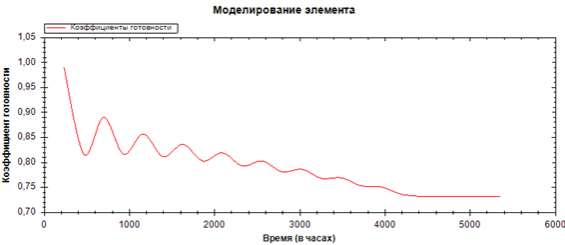
Рис. 10. Моделирование с экспоненциальным распределением времени отказа и восстановления
Таким образом, коэффициент готовности равен примерно 0,74. Поведение коэффициента готовности, полученного имитационным моделированием, подтверждается расчетом, проведенным по аналитической модели, так приведем пример расчета по формуле 1. Параметры закона распределения приведены в табл. 1.
Таблица 1
Параметры законов распределения
|
Математическое ожидание нар-ки до отказа |
Среднее квадратическое отклонение наработки до отказа |
Математическое ожидание аварийного восстановления |
Среднее квадратическое отклонение аварийного восстановления |
|
0.4 |
0.1 |
0.1 |
0.02 |
Заключение
В результате проведенной работы были получены следующие результаты:
− Рассмотрены методы моделирования случайных величин, выполнено моделирование случайных величин, распределенных по нормальному и экспоненциальному закону.
− Описана модель обслуживания системы со стратегией последовательных восстановлений после отказов.
− Разработана имитационная модель позволяющая рассчитывать коэффициент готовности с требуемой точностью. Следует отметить, что точность в пятом знаке после запятой требует около часа времени работы современного компьютера. Правильность моделирования подтверждена расчетами, полученными для аналитической модели, описывающей данную стратегию работы системы.
− Отмечено, что неасимптотический коэффициент готовности стремится к асимптотическому тем быстрее, чем меньше время отказа системы, а также при экспоненциальном законе распределения.
Результаты работы могут быть использованы для расчета характеристик надежности сложных структур, в качестве модели отдельного элемента системы.
Литература:
1. Черткова, Е. А. Программная инженерия. Визуальное моделирование программных систем: учебник для академического бакалавриата / Е. А. Черткова. — 2-е изд., испр. и доп. — М.: Издательство Юрайт, 2019. — 147 с.
2. Девятков, В. В. Имитационное моделирование: Учебное пособие / Н. Б. Кобелев, В. А. Половников, В. В. Девятков. — М.: КУРС, НИЦ ИНФРА-М, 2013. — 368 c.
3. Волкова В. Н. Моделирование систем и процессов: учебник для академического бакалавриата / В. Н. Волкова [и др.]; под редакцией В. Н. Волковой, В. Н. Козлова. — М.: Издательство Юрайт, 2019. — 450 с.
4. Стельмашонок Е. В. Моделирование процессов и систем: учебник и практикум для академического бакалавриата / под редакцией Е. В. Стельмашонок. — М.: Издательство Юрайт, 2019. — 289 с.
Ключевые слова
восстановление, отказ, обслуживание систем, стратегии функционирования, коэффициент готовностиПохожие статьи
Метод наименьших квадратов в оценке параметров надежности...
Для определения математического ожидания и среднеквадратичного отклонения для каждого разряда статистического ряда подсчитывают qi с использованием выражения и по таблице квантилей нормального закона распределения определяют значения квантилей [2, 3].
Шаблон Excel для проверки законов распределения данных...
В статье рассматривается процедура создания шаблона Excel и опыт его применения для автоматического построения гистограмм и кривых Гаусса по результатам данных экспериментальных наблюдений с одновременной оценкой согласия по критерию Пирсона в...
Метод улучшения оценок метода максимального правдоподобия...
% обратная функция максимального правдоподобия для нормального закона.
где — математическое ожидание случайной величины , — среднее квадратическое отклонение.
максимальное правдоподобие, экспоненциальное распределение, математическое...
Особенности анализа характеристик видеотрафика в системе АМС
Рис. 5. Зависимость среднеквадратичного отклонения размеров очереди от коэффициента загрузки.
Средние размеры очередей зависят, по отдельности, не от распределения интервалов между заявками и распределения интервалов обработки, а от их совокупности.
Вычисление статистических показателей с использованием...
Основные термины (генерируются автоматически): нормальное распределение, Коэффициент эксцесса, Коэффициент асимметрии, среднее, Коэффициент
— коэффициент вариации. где — оценка среднеквадратического отклонения всех случайных величин в выборке.
Решение задач анализа и синтеза на имитационных моделях...
Приведено математическое описание случайной величины — длительности раскроя сырья на
Например, распределение интервалов времени выполнения операций раскроя сырья и полуфабрикатов
С распределением Эрланга и экспоненциальным согласуется только 16,1...
Статические обработки результатов наблюдений при проведении...
В случае нормального распределения вероятность того, что случайная величина примет значения в промежутке может быть вычислена по формуле [6]: где — математическое ожидание случайной величины , — среднее квадратическое отклонение.
Проверка нормальности распределения оценок параметров...
причём математическое ожидание случайной величины ε равно нулю.
Величины характеризуют отклонение регрессионной модели от измеренных откликов.
— выборочная оценка среднеквадратичного отклонения, — выборочное среднее, N — объём выборки.
Математические модели и методы обработки информации...
максимальное правдоподобие, экспоненциальное распределение, математическое
где ; — математическое ожидание случайной величины (практически равно среднему значению цикла
Коэффициент асимметрии характеризует смещение распределения относительно...
Определение значимости угроз в модели угроз безопасности при...
Рис. 10. Обратная функция распределения для модели с треугольным распределением.
Для нормального распределения эти величины нулевые .
Математическое ожидание для данного распределения равно , значение дисперсии , значение среднего квадратического...
Похожие статьи
Метод наименьших квадратов в оценке параметров надежности...
Для определения математического ожидания и среднеквадратичного отклонения для каждого разряда статистического ряда подсчитывают qi с использованием выражения и по таблице квантилей нормального закона распределения определяют значения квантилей [2, 3].
Шаблон Excel для проверки законов распределения данных...
В статье рассматривается процедура создания шаблона Excel и опыт его применения для автоматического построения гистограмм и кривых Гаусса по результатам данных экспериментальных наблюдений с одновременной оценкой согласия по критерию Пирсона в...
Метод улучшения оценок метода максимального правдоподобия...
% обратная функция максимального правдоподобия для нормального закона.
где — математическое ожидание случайной величины , — среднее квадратическое отклонение.
максимальное правдоподобие, экспоненциальное распределение, математическое...
Особенности анализа характеристик видеотрафика в системе АМС
Рис. 5. Зависимость среднеквадратичного отклонения размеров очереди от коэффициента загрузки.
Средние размеры очередей зависят, по отдельности, не от распределения интервалов между заявками и распределения интервалов обработки, а от их совокупности.
Вычисление статистических показателей с использованием...
Основные термины (генерируются автоматически): нормальное распределение, Коэффициент эксцесса, Коэффициент асимметрии, среднее, Коэффициент
— коэффициент вариации. где — оценка среднеквадратического отклонения всех случайных величин в выборке.
Решение задач анализа и синтеза на имитационных моделях...
Приведено математическое описание случайной величины — длительности раскроя сырья на
Например, распределение интервалов времени выполнения операций раскроя сырья и полуфабрикатов
С распределением Эрланга и экспоненциальным согласуется только 16,1...
Статические обработки результатов наблюдений при проведении...
В случае нормального распределения вероятность того, что случайная величина примет значения в промежутке может быть вычислена по формуле [6]: где — математическое ожидание случайной величины , — среднее квадратическое отклонение.
Проверка нормальности распределения оценок параметров...
причём математическое ожидание случайной величины ε равно нулю.
Величины характеризуют отклонение регрессионной модели от измеренных откликов.
— выборочная оценка среднеквадратичного отклонения, — выборочное среднее, N — объём выборки.
Математические модели и методы обработки информации...
максимальное правдоподобие, экспоненциальное распределение, математическое
где ; — математическое ожидание случайной величины (практически равно среднему значению цикла
Коэффициент асимметрии характеризует смещение распределения относительно...
Определение значимости угроз в модели угроз безопасности при...
Рис. 10. Обратная функция распределения для модели с треугольным распределением.
Для нормального распределения эти величины нулевые .
Математическое ожидание для данного распределения равно , значение дисперсии , значение среднего квадратического...











