Ставится задача об одиночной популяции, подверженной промыслу. Исследуется двухпараметрическая математическая модель, предложенная Джеймсом Марри. Построена область параметров, в которой существуют несколько стационарных решений для точечной модели. Доказано, что для диффузионной модели на линейном ареале могут существовать стационарные периодические решения.
Ключевые слова: популяция, краевые задачи, математическое моделирование.
Введение. В исследованиях Вольтерра [4] в первой половине XX века были заложены основы математической популяционной биологии. К сегодняшнему дню его последователями предложено много работ, в которых предлагаются различные трофические функции для взаимодействующих популяций, разработаны новые математические модели [3, 6, 10–12, 17, 25, 29, 31, 32, 52, 63, 64]. Большая часть моделей, представляет собой задачу Коши для системы обыкновенных дифференциальных уравнений. Реальные популяции живут на территориях, как с различными свойствами среды, так и с внутренней социальной организацией в разных ее частях [2, 18]. Это вызывает распространение особей по территории [5, 15, 16, 18, 35, 42, 43]. В математических моделях среда обитания считается сплошной, что позволяет использовать аппарат дифференциальных уравнений в частных производных, широко применяемый при разработке математических моделей агрессивных сплошных сред с нелинейными свойствами [7, 8, 13, 14, 19, 21, 22, 26–28, 38–41, 45–51, 59, 61, 63, 65, 66, 68].
Наиболее часто в литературных источниках встречаются модели для популяций, взаимодействующих по принципу хищник-жертва [3, 6, 33] или конкурирующих популяций [32]. Значительно реже встречаются модели для одиночной популяции [17, 25, 29, 31, 32, 34, 44, 53, 60]. В работе рассматривается модель одиночной логистической популяции, подверженной промыслу, предложенная в работах [60, 64]. Изъятие части популяции из отдельных зон ареала, как показывают полевые наблюдения, обычно не приводит к ее гибели. Со временем за счет миграции из соседних областей происходит восстановление ее численности [54]. Однако интенсивный промысел может привести к нарушению экологического равновесия в ареале с немалыми экономическими потерями [24, 37]. На практике регулирование численности популяции осуществляется с помощью квот. В теоретических исследованиях предлагаются различные подходы, используемые при управлении техническими системами [1, 20, 55–58, 67]. Однако в моделях такого рода не учитываются внутренние процессы, происходящие в популяции и приводящие к изменению стратегии их выживания. В результате даваемый на основе таких моделей прогноз о состоянии системы в будущем может быть даже ошибочным [23, 24].
В работе анализируется вариант промысла, при котором могут существовать несколько стационарных состояний. При этом устойчивым стационарным состоянием может оказаться состоянии с минимальной численностью популяции.
Модель логистической популяции, подверженной промыслу. В работе [60] в качестве математической модели одиночной популяции было предложено уравнение
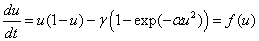 , (1)
, (1)
в котором 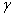 и
и 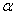 положительные постоянные, характеризующие уровень изъятия популяции. При
положительные постоянные, характеризующие уровень изъятия популяции. При 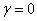 уравнение (1) переходит в уравнение для логистической популяции, существующей на неограниченном трофическом ресурсе.
уравнение (1) переходит в уравнение для логистической популяции, существующей на неограниченном трофическом ресурсе.
Стационарной точкой уравнения (1) является 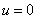 . Поскольку в этой точке
. Поскольку в этой точке 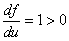 , то она будет неустойчивой: в ее малой окрестности функция
, то она будет неустойчивой: в ее малой окрестности функция 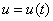 будет возрастающей функцией времени. В точке
будет возрастающей функцией времени. В точке 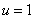 функция
функция 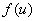 вместе со своей производной
вместе со своей производной 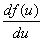 принимает отрицательные значения. Поэтому при
принимает отрицательные значения. Поэтому при 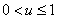 уравнение (1) будет иметь хотя бы одну стационарную точку. Если функция
уравнение (1) будет иметь хотя бы одну стационарную точку. Если функция 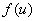 имеет кроме максимума еще и минимум, то уравнение
имеет кроме максимума еще и минимум, то уравнение 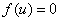 может иметь еще два нетривиальных корня. То есть необходимым условием существования минимума в точке, в которой функция
может иметь еще два нетривиальных корня. То есть необходимым условием существования минимума в точке, в которой функция 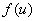 обращается в ноль (условие существования кратного корня), является одновременное выполнение неравенств
обращается в ноль (условие существования кратного корня), является одновременное выполнение неравенств
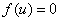 и
и 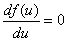
или
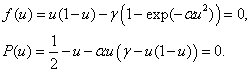 (2)
(2)
Второе уравнение является полиномом третьей степени. При этом
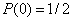 ,
, 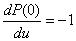 .
.
То есть в точке 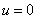 этот полином положителен и является убывающей функцией.
этот полином положителен и является убывающей функцией.
При 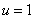 полином
полином 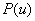 является убывающей функцией, поскольку
является убывающей функцией, поскольку 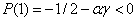 и
и 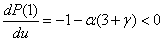 .
.
При 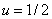
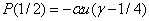 и
и 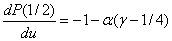 . Если выполняется неравенство
. Если выполняется неравенство 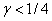 , то в этой точке полином
, то в этой точке полином 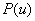 будет принимать положительные значения и будет возрастающей функцией при значениях параметра
будет принимать положительные значения и будет возрастающей функцией при значениях параметра 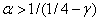 . В этом случае при
. В этом случае при 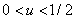 полином
полином 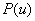 будет иметь минимум. Если этот минимум будет отрицательным, то полином будут иметь три корня: два на промежутке
будет иметь минимум. Если этот минимум будет отрицательным, то полином будут иметь три корня: два на промежутке 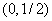 и один на промежутке
и один на промежутке 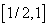 и, соответственно уравнение (1) будет иметь три стационарные точки. В этом случае экстремумы полинома достигаются в точках
и, соответственно уравнение (1) будет иметь три стационарные точки. В этом случае экстремумы полинома достигаются в точках
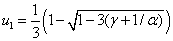 и
и 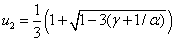 .
.
При значениях параметра 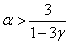 точки экстремума будут лежать внутри промежутка
точки экстремума будут лежать внутри промежутка 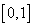 . Первый корень не превышает значения
. Первый корень не превышает значения 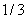 . При
. При 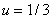
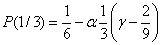 принимает отрицательное значение при
принимает отрицательное значение при 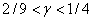 , если
, если 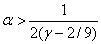 . Минимальное значение правой части этого неравенства достигается при
. Минимальное значение правой части этого неравенства достигается при 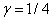 и равно 18. Таким образом, можно найти такие значения
и равно 18. Таким образом, можно найти такие значения 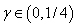 и
и 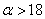 , при которых система уравнений (2) будет иметь хотя бы одно решение и, соответственно, уравнение (1) будет иметь три стационарные точки.
, при которых система уравнений (2) будет иметь хотя бы одно решение и, соответственно, уравнение (1) будет иметь три стационарные точки.
На рис. 1 в системе координат 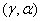 сплошной линией отображена граница раздела между областями, в которых существует одна и три стационарные точки. Вид функции
сплошной линией отображена граница раздела между областями, в которых существует одна и три стационарные точки. Вид функции 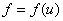 с тремя корнями на промежутке
с тремя корнями на промежутке 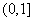 отображен на рис. 2 (
отображен на рис. 2 (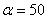 ,
, 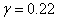 ). Нулевая стационарная точка
). Нулевая стационарная точка 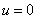 и точка
и точка 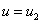 будут неустойчивыми, а точки
будут неустойчивыми, а точки 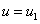 и
и 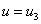 будут устойчивыми.
будут устойчивыми.
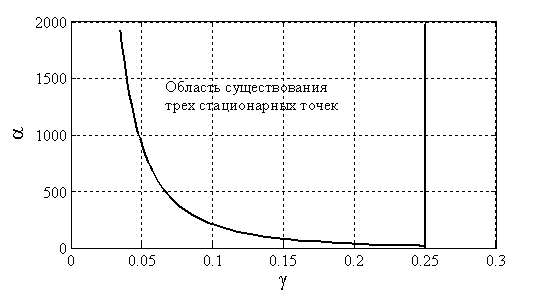
Рис. 1. Граница раздела между областями, в которых существует одна и три стационарные точки уравнения (1).
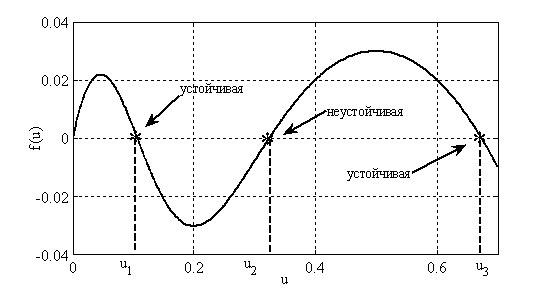
Рис. 2. Вид функции 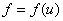 с тремя корнями на промежутке
с тремя корнями на промежутке 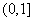 (
(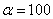 ,
,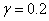 )
)
Диффузионная модель. Вприроде все живое живет на ограниченной территории. Геометрические формы ареалов могут быть самыми разнообразными — долины рек, горные хребты, обочины дорог [2, 15, 16, 18, 35, 42, 43], представляющие собой протяженные в одном направлении ареалы. В математической модели такой ареал можно представить в виде отрезка прямой [3, 11, 12, 17]. В этом случае для описания распространения особей можно использовать эволюционное уравнение [3, 52, 64, 68]
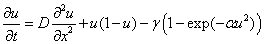 , (3)
, (3)
где 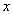 — декартова координата, а параметр
— декартова координата, а параметр 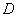 характеризует подвижность особей. В этой модели предполагается, что перемещение особей на отрезке происходит случайным образом [52].
характеризует подвижность особей. В этой модели предполагается, что перемещение особей на отрезке происходит случайным образом [52].
К уравнению (3) для случая отрезка длиной 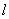 необходимо добавить начальные и граничные условия. В качестве начальных условий задается значение функции
необходимо добавить начальные и граничные условия. В качестве начальных условий задается значение функции 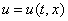 в начальный момент времени: при
в начальный момент времени: при 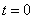
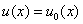 .
.
В качестве граничных условий рассматриваются условие наполнения среды [52]:
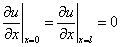 . (4)
. (4)
Условие обращения в ноль производной 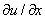 на границах отрезка допускает свободный рост численности популяции в этих точках.
на границах отрезка допускает свободный рост численности популяции в этих точках.
Если в качестве начальных условий для уравнения (3) взять 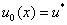 , где
, где 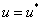 корни уравнения
корни уравнения 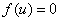 , то функция
, то функция 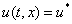 будет решением этого уравнения при граничных условиях (4). Если уравнение
будет решением этого уравнения при граничных условиях (4). Если уравнение 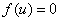 имеет несколько решений, то и уравнение (3) при граничных условиях (4) может иметь неединственное решение.
имеет несколько решений, то и уравнение (3) при граничных условиях (4) может иметь неединственное решение.
Стационарное решение. Уравнение (3) при 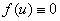 переходит в уравнение диффузии и его решение при стационарных граничных условиях со временем стремится к решению статической задачи независимо от значения искомой функции в начальный момент времени [52]. При рассматриваемых вариантах граничных условий (4) это будет тривиальное решение. Для нелинейного уравнения (3) это свойство может отсутствовать.
переходит в уравнение диффузии и его решение при стационарных граничных условиях со временем стремится к решению статической задачи независимо от значения искомой функции в начальный момент времени [52]. При рассматриваемых вариантах граничных условий (4) это будет тривиальное решение. Для нелинейного уравнения (3) это свойство может отсутствовать.
Стационарное решение нелинейного уравнения (3) должно удовлетворять дифференциальному уравнению
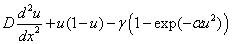 . (5)
. (5)
Это уравнение при естественном требовании 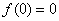 , накладываемом на функцию
, накладываемом на функцию 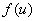 , при граничных условиях (4) будет иметь тривиальное решение.
, при граничных условиях (4) будет иметь тривиальное решение.
Если уравнение (5) умножить на 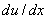 и проинтегрировать, то можно получить квадратуру [17]
и проинтегрировать, то можно получить квадратуру [17]
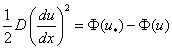 , (6)
, (6)
где 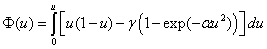 ,
,
а 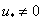 — значение функции
— значение функции 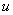 в точке
в точке 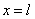 . Такой выбор постоянной интегрирования
. Такой выбор постоянной интегрирования 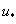 обеспечивает выполнение граничного условия при
обеспечивает выполнение граничного условия при 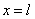 в (4). Если функция
в (4). Если функция 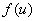 на промежутке
на промежутке 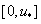 неотрицательна, то
неотрицательна, то 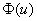 в силу этого будет монотонно возрастающей функцией с экстремальным значением в точке
в силу этого будет монотонно возрастающей функцией с экстремальным значением в точке 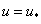 (при
(при 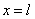 ).
).
При наличии трех нетривиальных стационарных точек 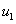 ,
, 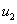 и
и 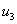 (рис. 2) функция
(рис. 2) функция 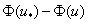 на отрезке
на отрезке 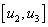 имеет экстремумы в точках
имеет экстремумы в точках 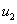 и
и 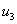 . Поэтому
. Поэтому 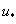 должно удовлетворять ограничениям
должно удовлетворять ограничениям 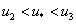 .
.
В этом случае из (6) следует зависимость между 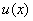 и
и 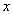 :
:
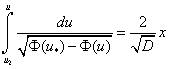 . (7)
. (7)
Длина отрезка 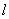 , на левом крае которого выполняется условие
, на левом крае которого выполняется условие 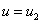 , а на правом
, а на правом 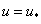 подсчитывается по формуле
подсчитывается по формуле
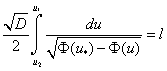 .
.
Интеграл в правой части этого выражения будет сходиться, поскольку функция 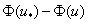 имеет ноль первого порядка только при
имеет ноль первого порядка только при 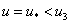 . При этом на построенном решении
. При этом на построенном решении 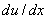 обращается в ноль на границах промежутка. То есть построенное нетривиальное решение будет удовлетворять условиям (4). Такое решение можно продолжить на бесконечную прямую.
обращается в ноль на границах промежутка. То есть построенное нетривиальное решение будет удовлетворять условиям (4). Такое решение можно продолжить на бесконечную прямую.
Устойчивость равновесных состояний. Стационарное уравнение (6) при наличии четырех корней у функции 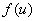 на промежутке
на промежутке 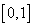 наряду с решениями
наряду с решениями 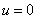 ,
, 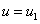 ,
, 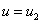 и
и 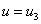 (рис. 2) может иметь периодические решения на бесконечной прямой. Пусть наряду с одним из этих решений существует близкое к нему решение
(рис. 2) может иметь периодические решения на бесконечной прямой. Пусть наряду с одним из этих решений существует близкое к нему решение 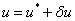 такое, что
такое, что 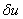 — малая по сравнению с единицей величина [17, 27, 31]. Тогда из уравнения (3) с точностью до величин второго порядка малости следует уравнение для
— малая по сравнению с единицей величина [17, 27, 31]. Тогда из уравнения (3) с точностью до величин второго порядка малости следует уравнение для 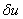
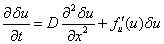 (8)
(8)
с начальным условием 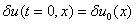 , где
, где 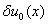 — малое отклонение от положения равновесия такое, что
— малое отклонение от положения равновесия такое, что 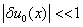 .
.
Для случая граничных условий (4) решение уравнения (8) представляется в виде тригонометрического ряда
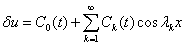 ,
, 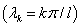 .
.
После подстановки этого выражения для 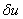 в уравнение (8), последующего умножения на
в уравнение (8), последующего умножения на 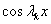 (
(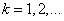 ) и интегрирования по промежутку
) и интегрирования по промежутку 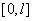 будут получены уравнения для
будут получены уравнения для 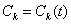 :
:
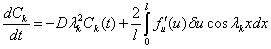
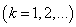 ,
,
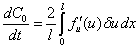 .
.
Уравнение для 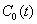 при
при 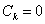 (
(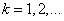 ) принимает вид
) принимает вид
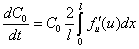 .
.
Отсюда следует, что при положительных значениях 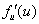 функция
функция 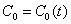 будет возрастающей функцией времени и соответствующее стационарное решение будет неустойчивым. То есть решения
будет возрастающей функцией времени и соответствующее стационарное решение будет неустойчивым. То есть решения 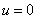 ,
, 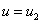 (рис. 2) и нетривиальное стационарное решение (7) будут неустойчивыми.
(рис. 2) и нетривиальное стационарное решение (7) будут неустойчивыми.
Численные эксперименты. Построение аналитических решений нелинейных эволюционных задач не представляется возможным. Для построения численного решения дифференциальных уравнений используются различные методы аппроксимации решений. Один из них — аппроксимация непрерывной функции сеточной и дискретизация дифференциальных операторов [27, 36, 62] с последующим сведением решения краевой задачи для дифференциальных уравнений к решению системы нелинейных трансцендентных уравнений. Анализ численных результатов решения нелинейных эволюционных уравнений различными методами, проведенный в [33], показал, что для непрерывных трофических функций результаты совпадают с высокой степенью точности. Но в тех случаях, когда существуют автоволновые решения [9, 22, 30, 64] наиболее эффективными являются сеточные методы. Один из вариантов сеточных методов реализован в виде «встроенной» функции в математическом пакете MatLab.
Построение численного решения уравнения (3) при граничных условиях (4) осуществлялось в среде программирования математического пакета MatLab с применением встроенной функции pdepe, в которой используются сеточные методы решения краевых задач. В качестве начальных условий бралась функция 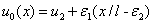 , где
, где 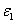 и
и 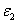 малые положительные величины, а
малые положительные величины, а 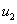 — стационарное решение уравнения (1) (рис. 2). То есть при
— стационарное решение уравнения (1) (рис. 2). То есть при 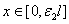 функция
функция 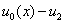 принимает отрицательные значения, а при
принимает отрицательные значения, а при 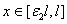 — положительные. Такое начальное распределение представляет собой малое отклонение от стационарного решения
— положительные. Такое начальное распределение представляет собой малое отклонение от стационарного решения 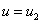 , которое является неустойчивым.
, которое является неустойчивым.
Результаты численного решения для случая 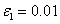 ,
, 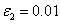 ,
, 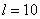 ,
, 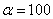 ,
, 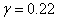 ,
, 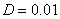 в различные моменты времени в виде зависимостей
в различные моменты времени в виде зависимостей 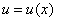 представлены на рис. 3. Как следует из полученного результата при малых отклонениях от стационарного решения таких, что численность популяции в малой окрестности точки
представлены на рис. 3. Как следует из полученного результата при малых отклонениях от стационарного решения таких, что численность популяции в малой окрестности точки 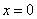 уменьшается (
уменьшается (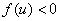 ), а на остальной части увеличивается (
), а на остальной части увеличивается (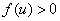 ). На начальном временном интервале (
). На начальном временном интервале (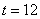 ,
, 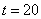 ) на левом крае значение функции
) на левом крае значение функции 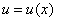 приближается к стационарному значению
приближается к стационарному значению 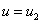 , а на правом — к
, а на правом — к 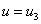 . Со временем происходит постепенный переход решения в стационарное состояние
. Со временем происходит постепенный переход решения в стационарное состояние 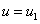 (
(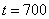 ). Таким образом, при незначительных отклонениях от неустойчивого стационарного положения равновесия на малой части пространственного ареала возможно уменьшение численности на всем ареале.
). Таким образом, при незначительных отклонениях от неустойчивого стационарного положения равновесия на малой части пространственного ареала возможно уменьшение численности на всем ареале.
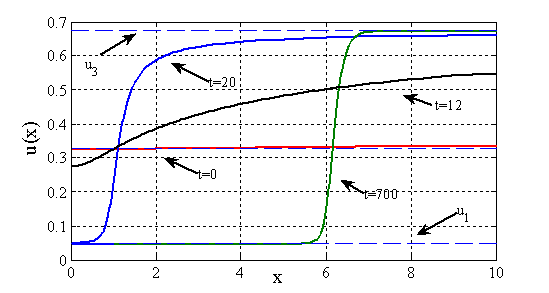
Рис. 3. Зависимость функции 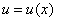 в моменты времени
в моменты времени 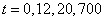 (
(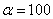 ,
, 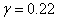 ,
, 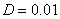 ).
).
Заключение. Таким образом, в рассматриваемой модели одиночной популяции, подверженной промыслу, существует два удаленных друг от друга распределения численности особей на отрезке при одном и том же способе «изъятия» особей. Переход между этими состояниями может происходить только «скачкообразно». Наиболее рациональный вариант промысла для такой модели — поддерживать численность популяции на более высоком уровне, поскольку переход из области с меньшей численностью в область с большей численности может потребовать немалых экономических затрат.
Как следует из полученных выше результатов из «диффузионной» модели одиночной популяции следуют результаты, не содержащиеся в «точечных» моделях — на бесконечной прямой могут существовать периодические решения стационарного уравнения.
Литература:
1. Алферов Г. В. Генерация стратегии робота в условиях неполной информации о среде // Проблемы механики и управления: Нелинейные динамические системы. — 2003. — № 35. — С. 4–23.
2. Аргунов А. В. Морфологические особенности и систематическое положение сибирской косули (capreolus pygargus pall., 1771) Якутии // Амурский зоологический журнал. — 2013. — Т. 5. — № 2. — С. 208–212.
3. Базыкин А. Д. Нелинейная динамика взаимодействующих популяций. Москва-Ижевск: Институт компьютерных технологий, 2003. — 368 с.
4. Вольтерра В. Математическая теория борьбы за существование. Москва-Ижевск:, Институт компьютерных технологий, 2004. — 288 с.
5. Вяткин П. С. Динамика Корякской популяции лося (alces alces linnaeus, 1758) // Амурский зоологический журнал. — 2012. — Т. 4. — № 1. — 403–410.
6. Гасратова Н А., Бойцов Д. С., Крылова В. А. Модель Базыкина хищник-жертва // Современные методы прикладной математики, теории управления и компьютерных технологий (ПМТУКТ-2014), сб. тр. VII междунар. конф. Воронеж: Издательство «Научная книга», 2014. С. 84–86.
7. Гасратова Н. А. Напряженно-деформированное состояние упругого пространства со сферическим жестким включением // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2009. — № 1. — С. 14–18.
8. Гасратова Н. А. Решение некоторых классических пространственных задач теории упругости в напряжениях // Молодой ученый. — 2014. — № 3 (62). — С. 1–6.
9. Гасратова Н. А., Бойцов Д. С., Габриелян Л. А., Тюганова Т. М. Математическая модель иммунного ответа организма млекопитающих на поражение кожи ожогом // Молодой ученый. — 2014. — № 12 (71). — С. 1–7.
10. Гасратова Н. А., Бойцов Д. С., Крылова В. А., Гаврилова А. В. Модель Базыкина-Свирежева хищник-жертва // Молодой ученый. — 2014. — № 12 (71). — С. 8–12.
11. Гасратова Н. А., Столбовая М. В., Бойцов Д. С., Степанова Д. С Математическая модель хищник-жертва на линейном ареале // Молодой ученый. — 2014. — № 11. — С. 1–10.
12. Гасратова Н. А., Столбовая М. В., Неверова Е. Г., Бербер А. С. Математическая модель «ресурс-потребитель» // Молодой ученый. — 2014. — № 10 (69). — С. 5–14.
13. Гасратова Н. А., Шамина В. А. Об одном подходе к решению осесимметричных задач линейной теории упругости // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2007. — № 2. — С. 101–106.
14. Гасратова Н. А., Шамина В. А. Решение в напряжениях линейной осесимметричной задачи для сферы и упругого пространства со сферической полостью // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2008. — № 2. — С. 122–128.
15. Гилев А. В. Закономерности пространственного распределения и научные основы охраны рыжих лесных муравьев // Зоологический журнал. — 2010. — Т. 89. — № 12. — С. 1413–1420.
16. Глушков В. М., Сафонов В. Г., Сергеев А. А., Шевнина М. С., Анализ динамики популяций лося на Южном Урале // Теоретическая и прикладная экология. — 2013. — № 2. — С. 153–160.
17. Горбунова Е. А., Колпак Е. П. Математические модели одиночной популяции // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления Сер. 10. — 2012. — Вып. 4. — С. 18–30.
18. Громов В. С. Пространственно-этологическая структура популяций грызунов. М.: Т-во научн. изданий КМК. 2008. 581 с.
19. Даль Ю. М., Пронина Ю. Г Сосредоточенные силы и моменты у границы упругой полуплоскости // Известия Российской академии наук. Механика твердого тела. — 1998. — № 5. — С. 78.
20. Жигальский О. А. Экологическое регулирование численности популяций мелких млекопитающих // Успехи современного естествознания. — 2013. — № 2. — С. 61–64.
21. Жукова И. В., Колпак Е. П. Математическая модель солидной опухоли // Естественные и математические науки в современном мире. — 2013. — № 13. — С. 18–25.
22. Жукова И. В., Колпак Е. П. Математические модели злокачественной опухоли // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2014. — № 3. — С. 5–18.
23. Ильичев В. Г. Оптимизация и пространственная адаптация в проблеме многолетнего вылова рыбных популяций // Проблемы управления. — 2014. — № 2. — С. 66–74.
24. Ильичев В. Г., Ильичева В. В. Пространственная адаптация и оптимальный промысел рыбных популяций // Экономика и математические методы. — 2014. — Т. 50. — № 3. — С. 119–129.
25. Колесин И. Д., Старков В. Н., Гасратова Н. А. Одиночная популяция под антропогенным давлением // Журнал научных публикаций аспирантов и докторантов. — 2014. — № 6 (96). — С. 226–232.
26. Колпак Е. П. Введение в механику сплошных сред учебное пособие / Е. П. Колпак; С.-Петерб. гос. ун-т. СПб. 2004.
27. Колпак Е. П. Устойчивость и закритические состояния безмоментных оболочек при больших деформациях // диссертация на соискание ученой степени доктора физико-математических наук / Санкт-Петербург, 2000.
28. Колпак Е. П., Балыкина Ю. Е., Котина Е. Д., Жукова И. В. Математическая модель нарушений функционирования щитовидной железы // Молодой Ученый. — 2014. — № 2 (61). — С. 19–24.
29. Колпак Е. П., Горбунова Е. А., Балыкина Ю. Е., Гасратова Н. А. Математическая модель одиночной популяции на билокальном ареале // Молодой ученый. — 2014. — № 1 (6). — С. 28–33.
30. Колпак Е. П., Горбунова Е. А., Жукова И. В. Математическая модель популяционной волны // Естественные и математические науки в современном мире. — 2014. — № 16. — С. 25–41.
31. Колпак Е. П., Горбунова Е. А., Столбовая М. В., Балыкина Ю. Е Математическая модель логистической популяции на линейном ареале // Молодой ученый. — 2014. — № 3 (62). — С. 6–14.
32. Колпак Е. П., Горыня Е. В., Полежаев В. Ю. Математическая модель конкуренции двух популяций (линейный ареал) [Текст] Колпак Е. П., Горыня Е. В., Полежаев В. Ю. // Сборник трудов VII Междунар. науч. конф. «Современные методы прикладной математики, теории управления и компьютерных технологий (ПМТУКТ-2014)». — Воронеж: Научная книга. 2014. — С. 206–209.
33. Колпак Е. П., Жукова И. В., Степанова Д. С., Крицкая А. В. О численных методах решения эволюционных уравнений на примере математической модели «хищник-жертва» // Молодой ученый. — 2014. — № 4 (63). — С. 20–30.
34. Колпак Е. П., Столбовая М. В. Математическая модель кинетики роста растений // Журнал научных публикаций аспирантов и докторантов. — 2013. — № 12 (90). — С. 230–232.
35. Коробченко М. А. Расширение ареала крота европейского (talpa europaea) в долине реки Северный Донец // Зоологический журнал. — 2009. — Т. 88. — № 4. — С. 465- 472.
36. Котина Е. Д. К теории определения поля перемещений на основе уравнения переноса в дискретном случае // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2010. — № 3. — С. 38–43.
37. Магомедов М.-З. Д., Яровенко Ю. А. Оценка состояния и особенности экологического мониторинга популяций крупных млекопитающих горных экосистем // Юг России: экология, развитие. — 2013. — Т. 3. — № 3 (28). — С. 82–99.
38. Мальков В. М., Малькова Ю. В. Анализ сингулярности напряжений в нелинейной задаче Фламана для некоторых моделей материала // Прикладная математика и механика. — 2008. — Т. 72. — № 4. — С. 652–660.
39. Мальков В. М., Малькова Ю. В. Нелинейная задача Фламана для материала Бартенева-Хазановича // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2005. — № 1–2. — С. 49–55.
40. Мальков В. М., Малькова Ю. В. Плоские задачи о сосредоточенных силах для полулинейного материала // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2013. — № 3. — С. 83–96.
41. Мальков В. М., Малькова Ю. В. Трещина в форме дуги окружности, расположенная вблизи поверхности раздела материалов // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2010. — № 1. — С. 93–104.
42. Мамонтов С. Н. Распределение по стволу дерева короеда-типографа (ips typographus, coleoptera, scolyniddae) и его энтомогафов // Зоологический журнал. — 2009. — Т. 88. — № 9. — С. 1139–1145.
43. Маркитан Л. В., Динкевич М. А. Современное состояние популяции орлана-белохвоста в дельте Дона, Россия // Пернатые хищники и их охрана. — 2013. — № 27. — С. 40–45.
44. Неверова Г. П., Жигальский О. Ф., Фрисман Е. Я. Моделирование динамики численности популяции рыжей полевки (Myodes Glareolus) // Региональные проблемы. — 2013. — Т. 16. — № 1. — С. 15–22.
45. Пронина Ю. Г Механохимическая коррозия полого цилиндра из идеального упруго-пластического материала под действием постоянного давления // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астроно-мия. — 2006. — № 3. — С. 121–130.
46. Пронина Ю. Г. Влияние поверхностных факторов на напряженно-деформированное состояние твердых тел с отверстиями // диссертация на соискание ученой степени доктора физико-математических наук / Санкт-Петербургский государственный университет. Санкт-Петербург, 2010.
47. Пронина Ю. Г. Краевая дислокация и сосредоточенная сила в упругой полуплоскости с отверстиями и краевыми вырезами // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2012. — № 4. — С. 120–124.
48. Пронина Ю. Г. О сосредоточенных воздействиях у границы упругой пластины // Труды ЦНИИ им. акад. А. Н. Крылова. — 2010. — № 53. — С. 117–122.
49. Пронина Ю. Г. Оценка устойчивости упругой трубы под давлением коррозионных сред // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2006. — № 3. — С. 55–63.
50. Пронина Ю. Г. Равномерная механохимическая коррозия полой сферы из идеального упругопластического материала под действием постоянного давления // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Ас-трономия. — 2009. — № 1. — С. 113–122.
51. Пронина Ю. Г. Расчет долговечности упругой трубы под действием продольной силы, давления и осесимметричного нагрева в условиях равномерной коррозии // Проблемы прочности и пластичности. — 2009. — № 71. — С. 129–135.
52. Ризниченко Г. Ю., Рубин А. Б. Биофизическая динамика продукционных процессов. Москва — Ижевск: Институт компьютерных технологий, 2004. — 464 с.
53. Родина Л. И. О некоторых вероятностных моделях динамики роста популяций // Вестник Удмуртского университета. Математика. Механика. Компьютерные науки. — 2013. — Вып. 4. — С. 109–124.
54. Русанов Я. С. Охота и охрана фауны (Влияние охоты на структуру популяций охотничьих животных). М.: Лесная промышленность. 1973. — 144 с.
55. Старков В. Н., Степенко Н. А. Исследование динамики маятниковых систем с переменными параметрами // Естественные и математические науки в современном мире. — 2014. — № 15. — С. 20–36.
56. Степенко Н. А О диссипативности неавтономных систем по нелинейному приближению // Вестник Санкт-Петербургского университета. Серия 10: Прикладная математика. Информатика. Процессы управления. — 2004. — № 3–4. — С. 160–169.
57. Степенко Н. А. О некоторых критериях диссипативности колебательных систем с переменными параметрами // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 2004. — № 1. — С. 50–54.
58. Шиманчук Д. В., Шмыров В. А. Пролблемы стабилизации орбитального движения космического аппарата в окрестности коллинеарной точки либрации // Молодой ученый. — 2014. — № 3 (62). — С. 20–24.
59. Balykina Y. E., Kolpak E. P., Kotina E. D Mathematical model of thyroid function // Middle East Journal of Scientific Research. — 2014. — Т. 19. — № 3. — С. 429–433.
60. Beddington J. R., May R. M. Harvesting natural populations in a randomly fluctuating // Science. — 1977. — V. 197. — P. 463–465.
61. Dal' Yu. M., Pronina Yu. G. On concentrated forces and moments in an elastic half-plane // Вестник Санкт-Петербургского университета. Серия 1: Математика. Механика. Астрономия. — 1998. — № 1. — С. 57–60.
62. Kotina E. D. Discrete optimization problem in beam dynamics // Nuclear Instruments and Methods in Physics Research. Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. — 2006. — Т. 558. — № 1. — С. 292–294.
63. McLeod P., Martin A. P., Richards K. J. Minimum length scale for growth — limited oceanic plankton distributions // Ecological Modeling. — 2002. — V. 158. — № 1–2. — P. 111–120.
64. Murray D. D. Mathematical biology. N. Y. Springer. 2002. — 551 p.
65. Pronina Y. Analytical solution for the general mechanochemical corrosion of an ideal elastic-plastic thick-walled tube under pressure // International Journal of Solids and Structures. — 2013. — Т. 50. — № 22–23. — С. 3626–3633.
66. Pronina Y. G. Estimation of the life of an elastic tube under the action of a longitudinal force and pressure under uniform surface corrosion conditions // Russian metallurgy (Metally). — 2010. — Т. 2010. — № 4. — С. 361–364.
67. Zhabko N. A. Some h-optimization problems for the iter plasma control system // International Journal of Modern Physics A. — 2009. — Т. 24. — № 5. — С. 1048–1056.
68. Zhukova I. V., Kolpak E. P., Balykina Y. E Mathematical model of growing tumor // Applied Mathematical Sciences. — 2014. — Т. 8. — № 29–32. — С. 1455–1466.







