В настоящее время традиционный взгляд на содержания обучения математике, ее роль и место, в общем, образования пересматриваются и уточняются.
Для продуктивной деятельности в современном информационном мире требуется достаточно прочная базовая подготовка, поэтому изучение темы «объемы фигур» очень актуально.
Проанализировав учебную программу по математике можно заметить, что основной целью изучения свойств геометрических тек в пространстве, является развитие пространственных представлений учащихся, освоение способов вычисления практически важных геометрических величин и дальнейшие развитие логического мышления учащихся. Умение изображать важнейшие геометрические тела, вычислять их площади поверхностей и объемы имеют большую практическую значимость.
Изучение темы «Объемы многогранников» дает возможность учащимся:
- получить представление о широте геометрии в различных областях человеческой деятельности;
- усвоить сведения о пространственных формах;
- использовать сведения из планиметрии для описания пространственных фигур;
- иллюстрировать пространственные формы, в частности решить задачи на сечения;
- решить различные задачи на вычислении;
- решить задачи на доказательства и т. д.
Задача вычисления объемов тел относится к глубокой древности. Они возникла в связи с практической деятельности людей. Объем-это часть пространство занимаемое телом. Понятие объема имеет следующие свойства:
- каждое тело имеет определенный объем;
- два равных многогранника имеют один и тот же объем;
- объем составного многогранника равен сумме объемов составляющих;
- если многогранник является частью другого многогранника, то его объем не больше объема этого многогранника;
- объем куба, ребро которого равно единице длины, равен единице.
Данное тело имеет объем,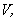 
если существуют содержащие его простые тела и содержащиеся в нем простые тела с объемами, сколь угодно мало отличающимися от 
.
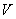Будем считать, что каждое из рассматриваемых нами тел имеет объем, который можно измерить с помощью выбранной единицы измерения объемов. За единицу измерения возьмем объем единичного куба. Куб с ребром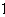 
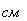называют кубическим сантиметром, 
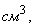также определяется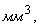 
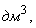
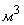и т. д. чтобы найти объём многогранника, нужно разбить его на кубы с ребром, равным единице измерения.
Использование наглядных моделей многогранников способствует решению разных дидактических задач. Они будут полезны на уроках геометрии. Наборы многогранников (каркасные модели, деревянных, из бумаги) демонстративны, дают необходимые представления о форме. Они могут служить объектами для измерения и определения площадей поверхностей объемов. Тела из стекла прозрачны и позволяют видеть элементы фигур, сечения тела, которые показывают либо стеклянными вкладышами, либо с помощью натянутых питей. Это модели могут демонстрироваться целому классу. С ними полезно поработать и отдельному ученику, пропустившему урок или занятому решением задач.
Рассмотрим метод вычисления объемов пространственных фигур, предложенный итальянским математиком Бонавентрой Кавальери (1598–1647) и названный впоследсвбим принсипом Кавальери. Он заключается в следующем.
Принцип Кавальери. Если при прессечении двух фигур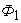 
и 
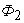в пространстве плоскостями, параллельными одной и той же плоскости, в сечениях получаются фигуры 
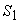и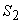 
одинаковой площади, то объемы исходных пространственных фигур равны.
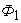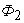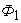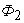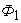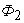Для обоснования этого принципа представим фигуры и составленными из тонких слоев одинаковой толщины, которые получаются при пересечение фигур и плоскостями, параллельными некоторой заданной плоскости. Считав слои прямыми цилиндрами, из равенства площадей их оснований и равенства высот получаем, что равные и объемы соответствующих слоев. Следовательно, равные объемы и составленной из этих слоев.
Теорема. Объем наклонного цилиндра равен произвведению площади его основания на высоту
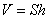
Доказательство. Для данного наклонного цилиндра с основанием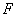 
площади 
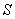и высотой 
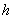расслютрим прямой цилиндр с таким же основанием и высотой. Расположим эти два цилиндра так, чтобы их основания находились на одной плоскости. Тогда сечения этих цилиндров плоскостями, параллельными этой плоскости, дадут фигуры, равные фигуре 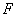и, следовательно, они будут иметь, отсюда следует равенство объемов цилиндров и, значит, для объема наклонного цилиндра имеет место формула: 
,
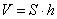где 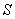- площадь основания, 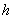- высота цилиндра.
Пусть 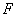- фигура на плоскости π, и 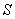- точка вне этой плоскости. Отрезки, соединяющие точки фигура 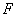с точкой 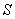, образуют фигуру в пространстве, которую мы будем называть конусом. Фигура 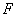называется основанием конуса, точка 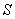- вершиной конуса. Перпендикуляр, опущенный из вершины конуса на плоскость основания, называется высотой конуса. По этому определению каждая пирамида также является конусом. Используя принцип Кавальери, докажем следующую теорему.
Теорема. Если два конуса имеют равных высоты основания равной площади, то их объемы равны.
Доказательство. Пуст конусы 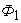и 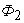имеют высоты, равные 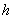, а основания площади 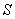расположение в одной плоскости π. При пересечение конусов плоскости параллельной основании получим 
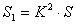и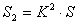 
т. е. они равны. Из принципа Кавальери получаем, что объемы конусов равны.
Если тело имеет правильную форму параллелепипеда, конуса, то для каждой из них имеется своя формула для вычисления объема. Но все эти формулы объединяет один математический принцип: произведения высоты фигуры на площадь ее основания.
Если тело имеет неровную, неправильную форму, то вычислить его объем можно при помощи измерительного сосуда и воды.
Еще один метод расчета объема тела любой формы и консистенции подразумевает знание массы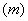 
и плотности 
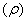этого тела. Объем тело в этом случал определяется по формуле: 
.
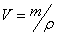Существование и единственность объема тела в школьном курсе математики приходится принимать без доказательства, так как вопрос об объемах принадлежит, по существу, к трудным разделам высшей математики. Поэтому нужные результаты устанавливаются, руководствуясь больше наглядными соображениями. Полезно иметь в кабинете и разбирающиеся наборы геометрических тел, сделанных из картона или плотной бумаги. Учащиеся могут самостоятельно изготовить разведка многогранников, также при изучении многогранников и их объемов можно использовать различные рабочие и справочные материалы. Рабочие таблицы — это такие таблицы, по материалу которых можно организовать активную мыслительную деятельность учащихся, как по усвоению нового материала, так и по его закреплению. С помощью рабочих таблиц, возможно, осуществить выполнение большого числа упражнений.
Литература:
1. Атанасян Л. С., Бутузов В. Ф., Кодомцев С.Б и др. Геометрия Учеб для 10–11кл. сред. шк. — М.: Просвещение, 1992.-207 с.
2. Калинин А. Ю., Терешин Д. А. Стереометрия. 10 класс. — М.:МФТИ, 1996 год.
3. Шклярский Д. О., Ченцов Н. Н., И. М. Избранные задачи и теоремы элементарной математики. Геометрия, Стереометрия.- М.: Физматлит. 2000–280с.
4. Шарыгин И. Ф. Геометрия. Стереометрия. Задачник. 10–11 классы-М.: Дрофа, 2000–272 с.
