Об изоморфизме групп Pin (0,1) и Pin (1,0)



В статье автор исследует изоморфизм групп Pin(0,1) и Pin(1,0). Приводится строгое математическое доказательство с использованием информации об алгебре Клифорда, а также конгруэнтность с циклическими группами . Приводится вся теоретическая база данного доказательства. В ходе работы было выявлено, что изоморфизм отсутствует.

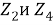
Ключевые слова: изоморфизм, спинорная группа, алгебра Клифорда.

Задача поиска изоморфизма в группах важна, потому что она позволяет установить эквивалентность между различными структурами и изучать их свойства на основе общих черт. Изоморфизм групп отражает их структурное сходство, что помогает упростить изучение и анализ свойств групп, а также облегчает решение задач и доказательство теорем.

Изоморфизм — это понятие в математике, обозначающее отношение между двумя объектами или системами, сохраняющее основные свойства и отношения между элементами этих объектов. Изоморфизм устанавливает соответствие между элементами двух систем таким образом, что каждому элементу первой системы соответствует единственный элемент второй системы, и наоборот.

Группой будем называть совокупность элементов, связанных между собой некоторой бинарной операцией, удовлетворяющей условиям ассоциативности и имеющей нейтральный элемент.

Группы Pin (n,m) будем называть спинорными группа алгебры Клифорда заданной сигнатуры .

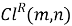
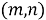
Алгебра Клиффорда — это унитальная ассоциативная алгебра, порождённая векторным пространством квадратичной формы. Она представляет собой обобщение действительных, комплексных чисел и кватернионов. Алгебра Клиффорда тесно связана с теорией квадратичных форм и ортогональных преобразований и имеет важные приложения в различных областях, таких как геометрия, теоретическая физика и цифровая обработка изображений.

Рассмотри доказательство с использование конгруэнтных отношений.

.

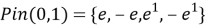
Получается, что данная группа находится в конгруэнтных отношениях с , где — прямое произведение.

.

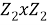
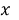
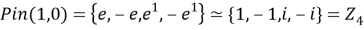
Единицей в данном случае будем называть пару чисел (1,1).

В случае единица имеет порядок

, а случае единица имеет уже порядок 4. Из этого можно сделать вывод, что изоморфизм между данными группами отсутствует.

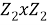
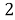
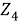
Теперь приведем доказательство построенное на базе алгебры Клифорда.

Алгебра Клифорда имеет генератор и соотношение .

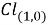
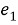
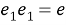
Алгебра Клифорда имеет генератор и соотношение .

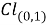
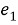
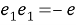
Получаем следующее:

,

.

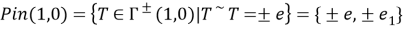
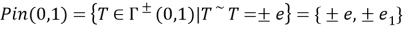
Будем использовать доказательство от противного. Предположим, что изоморфизм есть, тогда выполняется соотношение: .

Рассмотрим , который должен удовлетворять соотношению:

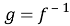
Но так как для любого элемента должно выполняться , а такого не существует. Поэтому эти группы не изоморфны.

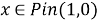
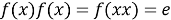
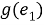
В ходе данной работы было выявлено, что группы Pin(0,1) и Pin(1,0) не изоморфны. Было приведено два различных доказательства этого факта. Отсутствие изоморфизма свидетельствует о том, что две системы или объекты не обладают полной структурной и функциональной эквивалентностью. Это указывает на различия в их организации и принципах работы, что может способствовать более глубокому пониманию их специфических характеристик и созданию более эффективных методов решения проблем, учитывающих индивидуальные особенности каждой системы или объекта.

Результаты данной научной работы могут найти применение в геометрии, физике и компьютерном зрении.

В дальнейшем имеет смысл рассмотреть матричный способ доказательства отсутствия изоморфизма данных групп. Так же возможно рассмотрение групп другой размерности, порожденные алгебрами Клифорда другой сигнатуры.

Литература:

1. Lounesto P., Clifford Algebras and Spinors, Cambridge Univ. Press (1997, 2001).

2. Рашевский П. К., Теория спиноров, УМН, 10:2(64), 3–110 (1955).

3. Румер Ю. Б., Спинорный анализ, М.-Л.: ОНТИ, (1936).

4. M. F. Atiyah, R. Bott, A.Shapiro, Clifford modules, Topology 3, pp. 3–38 (1964).

5. D.Hestenes, G.Sobczyk, Clifford Algebra to Geometric Calculus — A Unified Language for Mathematical Physics, Reidel Publishing Company (1984).

6. Marchuk N. G., Shirokov D. S., Unitary spaces on Clifford algebras, Advances in Applied Clifford Algebras, Volume 18, Number 2, pp. 237–254, (2008).

7. Широков Д. С., Классификация элементов алгебр Клиффорда по кватернионным типам, Доклады академии наук, т.427, 6, c.758–760 (2009).

8. Shirokov D. S., Quaternion typification of Clifford algebra elements, Advances in Applied Clifford Algebras, Online First (2011), arXiv:0806.4299v2 [math-ph].

9. Shirokov D. S., Development of the method of quaternion typification of clifford algebra elements, Advances in Applied Clifford Algebras, Online First (2011), arXiv:0903.3494v1 [math-ph].