В статье, как указанo в названии, показано применение метода n -прямых к решению некоторых задач и получено много интересных результатов, которые не были ранее опубликованы.
Рассмотрим способ деления сторон треугольника пропорционально n-м степеням прилежащих сторон
Пусть, задан треугольник ABC с соответствующими сторонами a, b, c. Проведем прямую CD с вершины С к стороне AB . Предположим, что точка D делит сторону AB = с пропорционально n -м степеням боковых сторон AC=b и BC =a . То есть, если введем обозначения AD=p , DB=q , то будет
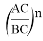
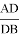
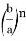

А теперь применим метод n прямых к решению ниже указанных задач:
1) Получим общую формулу для длины линии n прямых. Для этого используем формулу Стюарта (см. рис. 1):
Как известно, тогда
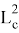
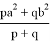
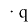
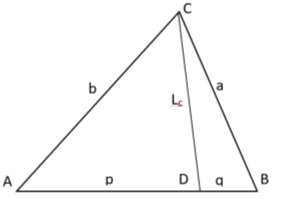
Рис. 1
По условию задачи пусть
p=k
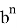
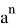
Тогда, p + q= k (
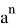
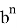
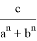
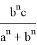
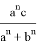
После подстановки этих значений в (1) получаем:
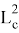
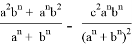
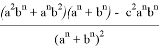
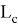
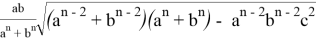
Аналогичные формулы можно получить для двух других n прямых, проведенных соответственно, из вершин треугольника A и B :
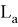
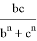
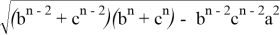
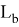
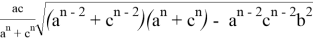
Покажем, что из этих формул можно получить формулы для длин медианы, биссектрисы, симедианы и антибиссектрисы треугольника ABC . Действительно, при n=0 из формулы (4) получаем формулу медианы:
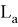
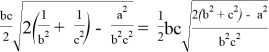
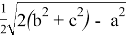
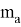
При n=1 получаем формулу биссектрисы:
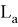
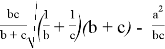
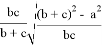
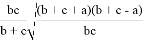
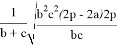
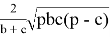
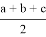
При n=2 получаем формулу для симедианы:
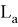
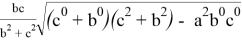
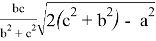
При n= -1 получаем формулу для антибиссектрисы:
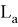
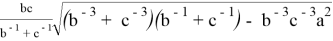
После некоторых преобразований получаем:
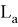
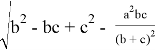
2) Используя метод n прямых, найдем некоторые формулы в вписанном четырехугольнике.
Предположим,
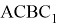
AC=b, BC=a, AB=c, A
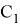
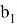
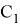
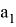
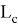
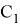
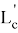
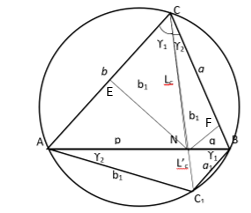
Рис. 2.
Пусть
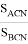

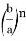
Учитывая, что
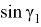
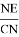
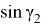
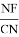
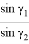
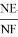
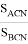
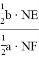
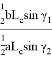
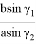
Откуда получаем
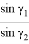

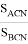
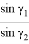

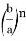
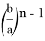
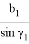
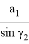
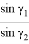


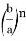
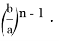
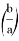



Соответствующим образом можно получить формулу
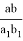

3) Выразим значения
p, q,
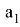
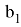
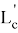
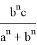
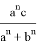
Из подобия треугольников ACN и B
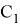


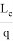
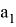
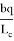
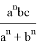
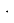

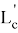
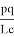
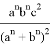
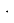

Из подобия треугольников
BCN
и
A
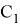
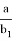
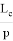

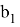
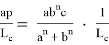
4) Определим степень
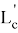
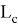
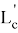
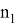
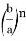
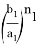


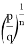

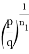

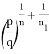


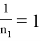
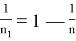
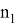
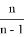
Следовательно, степень прямой
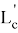
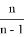
5) Определим степени прямых, находящихся на одинаковом расстоянии от высоты. Пусть СН является высотой, опущенной с вершины C в треугольнике
ABC
и точки
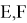
Предположим:
AH = b

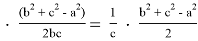
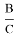
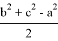
BH = a

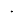

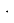

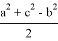
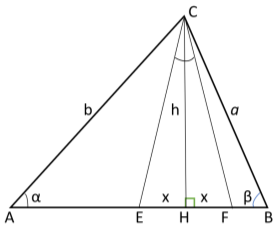
Рис. 3.
Предположим, степень
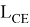
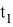
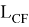
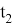
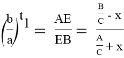
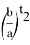
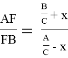
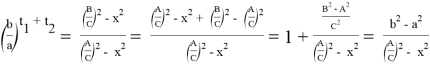
Здесь
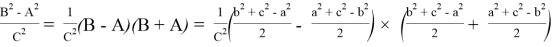
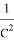
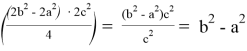
Из формулы (17) получаем:
x =
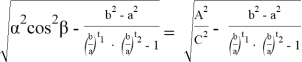
С другой стороны из
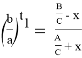
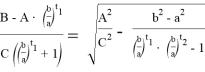
Пусть
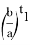
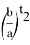
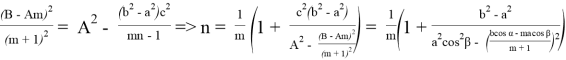
Следует отметить, что m и n симметричные переменные, т. е. можно поменять их местами.
Тогда, из (19) можно получить:
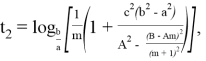
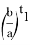
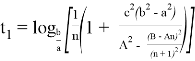
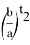
6) Из всего бесконечного числа n прямых наиболее важное значение принимает тот случай, когда прямая перпендикулярна основанию треугольника. Чтобы отличить эту прямую от других, обозначаем степень этой прямой через k , определим пределы изменения этого числа и выразим его через n .
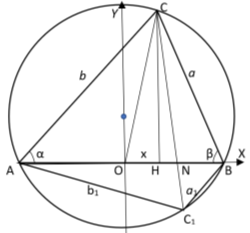
Рис. 4.
Предположим, дается треугольник ABC, где BC=a , AC=b , AB=c (рис.4).
Проведем из вершины С высоту СН и медиану СО. Тогда
AO=OB=



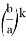
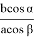
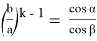
С другой стороны, из (8) можно написать
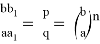
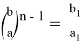
Разделив (22) на (21), получаем:
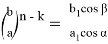
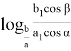
Предположим:
OH=x
, тогда AH =
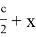
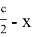
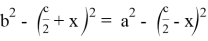
Упрощая последнее равенство, получаем:
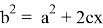
Преобразуем равенство
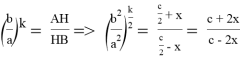
С другой стороны, из (24) получаем:
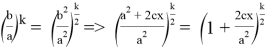
Приравнивая правые части (25) и (26) после преобразования, получаем:
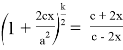
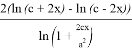
Установим к чему будет стремиться число
k
когда
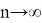
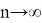
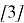
Вычислим следующий предел:
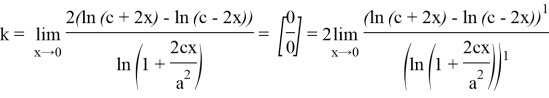
Так как, в равностороннем треугольнике
a=c,
то получаем k
=
4, то есть при
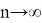
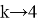
Теперь выясним к чему стремится число
k
, если
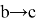
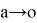
Вычислим следующий предел:
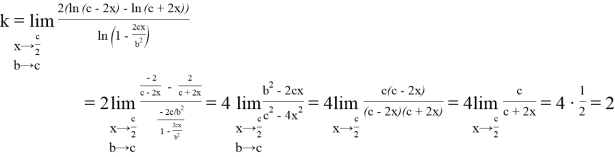
Следовательно, в указанном случае
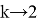
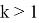
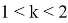
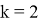
7) Изотомические и изогональные линии и связанные с ними формулы.
Как известно, две точки на стороне треугольника, равноудаленные от середины стороны, называются изотомическими точками. Две прямые, соединяющие вершину треугольника с изотомическими точками, лежащими на противоположной стороне, называются изотомическими. Две прямые, проходящие через вершину угла и образующие равные углы с биссектрисой угла, называются изогональными прямыми относительно сторон этого угла.
Прямые изогональные относительно углов треугольника -называются изогоналями треугольника. Также известно, что прямая изогональная прямой n , есть прямая ( 2 — n ).
Практически, чтобы найти прямую изогональную прямой n в треугольнике ABC , вокруг треугольника описываем окружность. Находим пересечение прямой n (прямая CN) с окружностью (точка Е ). (Рис. 5).
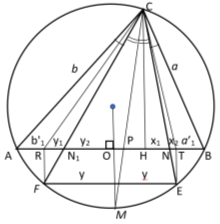
Рис. 5.
Далее проводим прямую EF, которая параллельна стороне AB. Так как она перпендикулярная,
AB
делит дугу
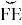
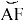
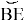
Следовательно, углы ∠ACF и ∠BCE равны.
То есть, прямые CE и CF изогональны и CP является биссектрисой треугольника ABC.
Кроме того, точки
R
и
T
являются изотомическими точками, и прямая
CR
является прямой (
2-n
). Пусть, прямая
CT —
это прямая
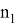
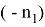
А теперь, напишем формулы для расстояния между точками пересечений изогональных и изотомический прямых с основанием треугольника. Предположим, как видно из рис.5.
AR=
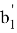
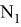
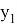
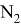
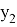
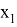
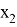
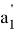
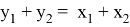
AN =
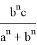
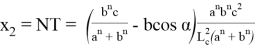
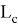
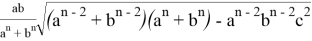
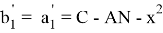
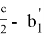
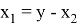
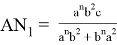
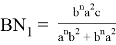
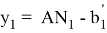
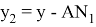
Следует отметить, что степень для прямой СТ определяется следующим образом.
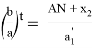
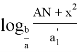
Тогда, степень для прямой CR равна (
-t
). Следует также отметить, что при
n=2
, то есть для прямоугольного треугольника получаем
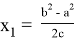
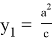
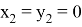
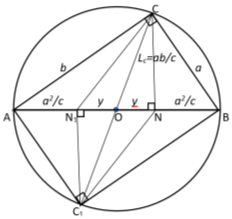
Рис. 6.
8) А теперь, рассмотрим случай, когда прямая n проходит через центр окружности. (рис.7)
Предположим, в треугольнике ABC
CN
имеет степень
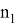
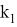
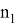
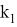
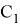
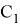
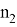
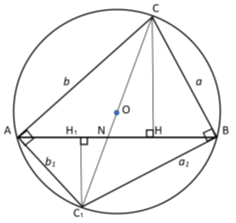
Рис. 7.
Тогда, используя формулу (22), можно написать:
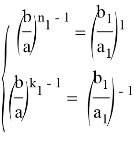
Далее используя известную формулу:
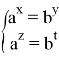


Мы получим
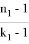
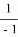
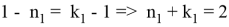
Точно также, для треугольника
A
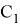
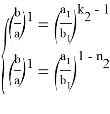
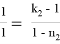
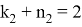
Можно также написать следующие формулы, которые нетрудно вывести:
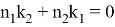
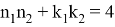
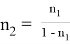
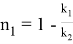
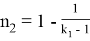
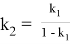
9) Из всех
n
прямых, наибольшее значение играет прямая для степени
n
которая выполняется равенством:
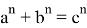
Здесь
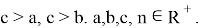
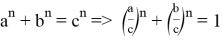
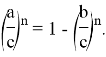
Рассмотрим функции
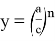
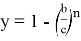
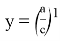
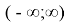
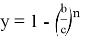
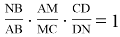
Здесь точка D является точкой пересечения n прямых.
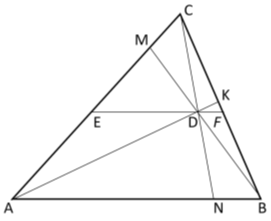
Рис. 8.
Из формулы (2) мы знаем, что
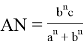
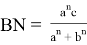
Если учесть здесь формулу (32), получаем
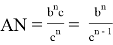
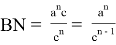
Подставляя (34) в (33), получаем:
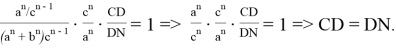
10) Учитывая важность значения
n
, при котором равенство
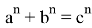
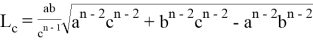
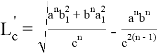
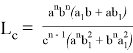
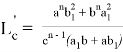
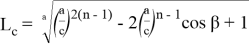
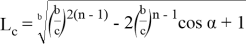
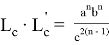
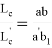
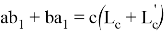
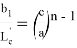
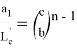
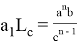
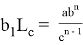
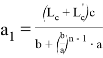
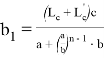
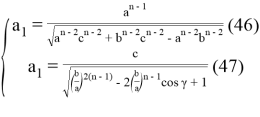
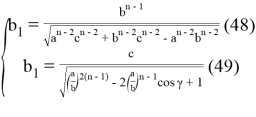
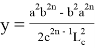
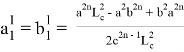
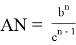
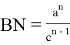
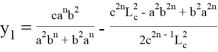
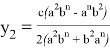
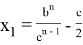
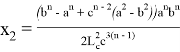
или
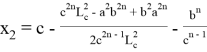
11). Пусть
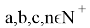
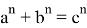
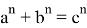
Действительно, как известно
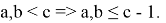
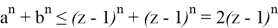
Используем неравенство Бернулли:
Если
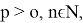
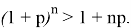
Следовательно,
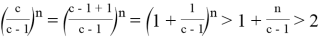
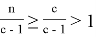
Тогда мы получаем:
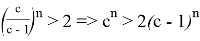
Если (57) учесть в (56), то получаем
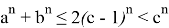
Далее, решим равенство (39), (40) относительно n . Тогда получаем:
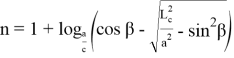
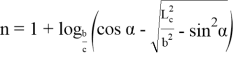
Учитывая (59) и (60) в (58), получаем:
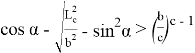
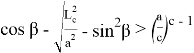
12) Покажем, что будет если
n
прямая (при выполнении
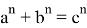
Пусть,
n=k
, то есть
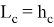
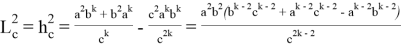
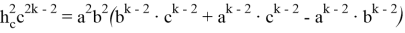
Здесь имеем:
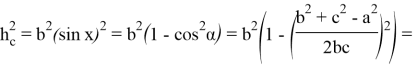
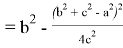
Подставляя (64) в (63), получаем:
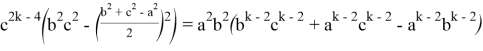
Здесь
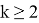
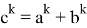
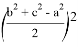
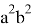
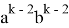
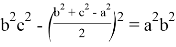
Если упростить данное выражение получаем:
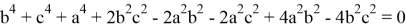
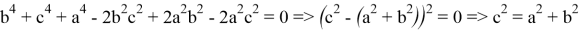
Что и следовало ожидать.
То есть, это важно только в прямоугольном треугольнике. В этом случае:
n = k = 2 .
13) Теперь постараемся ответить на вопрос о рациональности или иррациональности числа k . Как известно, в прямоугольном треугольнике k = 2 является целом числом. Пусть n > k > 2 . Как известно из формулы (21)
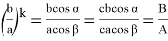
Здесь, как мы уже отмечали,
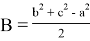
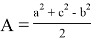
Так как для выполнения равенства
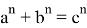
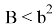
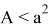
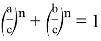
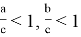
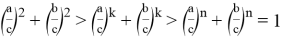
Следовательно, в этом случае
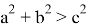
Из последнего следуем, что
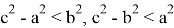
Тогда получаем:
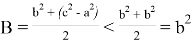
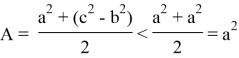
Следовательно, при n > k > 2 получаем:
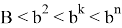
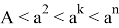
Если в формуле
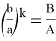
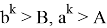
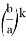

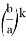
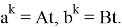
14) Найдем область изменения
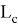
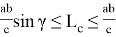
Как известно из (35):
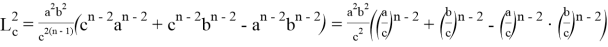
Предположим,
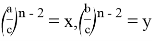
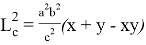
Проведем следующие преобразования:
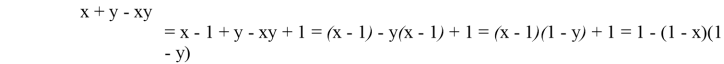
Так как
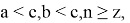
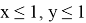
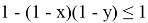
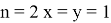
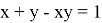
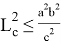
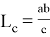
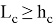
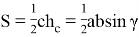
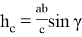
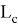
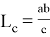
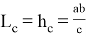
15) Используя формулу (39), покажем, что
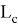
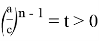
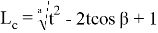
Для того чтобы
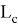
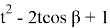
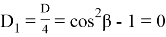
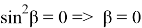
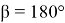
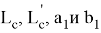
Это можно увидеть из формул (41) и (43). Однако квадрат этих чисел рационален.
16) Как известно, [1,2] n прямые, проведенные с вершины с треугольника ABC , соответственно при i = 0,1,2, …, n — 1, n , и т. д. будут выглядеть как на рис.9.
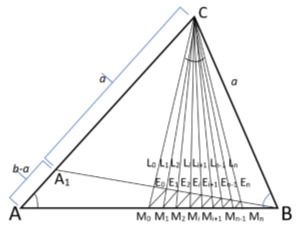
Рис. 9.
Здесь, длина линии:
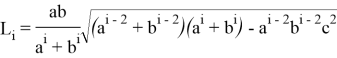
Здесь также расстояние
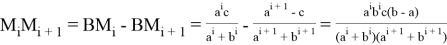
Например, при i = 0 мы получаем:
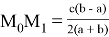
При i = 1,
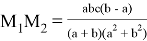
17) Если прямые
CN
и
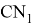
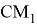
Действительно, так как
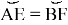
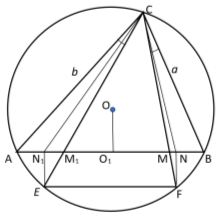
Рис. 10.
Следовательно,
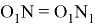
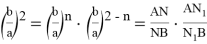
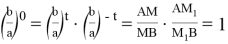
18) Выразим угол
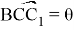
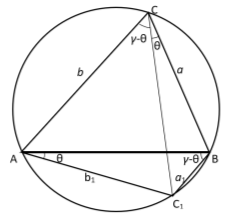
Рис. 11.
В треугольнике ABC, по теореме синусов получаем:
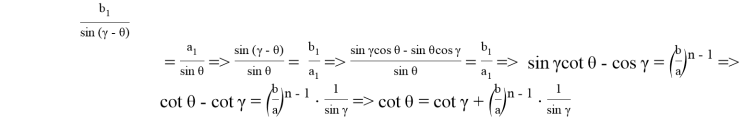
Эту же формулу можно получить из формулы (7).
Таким образом, в данной статье показано применение метода n прямых к решению некоторых вышеуказанных геометрических задач
Литература:
- Зетель С. И. Сборник статей по элементарной и началам высшей математики. Математическое просвещение, серия 1.1, 1934, с.5–8
- Зетель С. И. Новая геометрия треугольника. Пособие для учителей. Москва, 1962, с.120–129
- Elkhan Baylarov, Ilyas Hasanov. A Different Geometric Approach to the Proof of Fermat’s Last Theorem
- Richard Kaufman. Limits on Legs of Pythagorean Triples and Fermat’s Last Theorem. The College Mathematics Journal, 51:1, 2020, 53–56, Doi:10.1080/07468342, 2020/1674620
- Виктор Мещеряков. Электронные материалы. Прямые в треугольнике и Великая теорема Ферма. https://youtu . b e/ho MTCd8epMy , октябрь 2022
- Wiles, Andrew. Modular elliptic curves and Fermat’s Last Theorem. Annals of Mathematics, 141(3), 443–551, 1995
- Paulo Ribenboim. Fermat’s Last Theorem for Amateurs — Springer. Department of Mathematics and Statistics. Queen’s University. Kingston. Ontario/ K7L3N6. Canada







