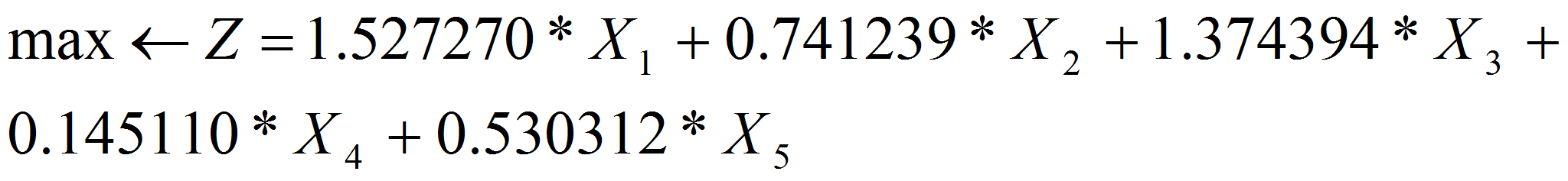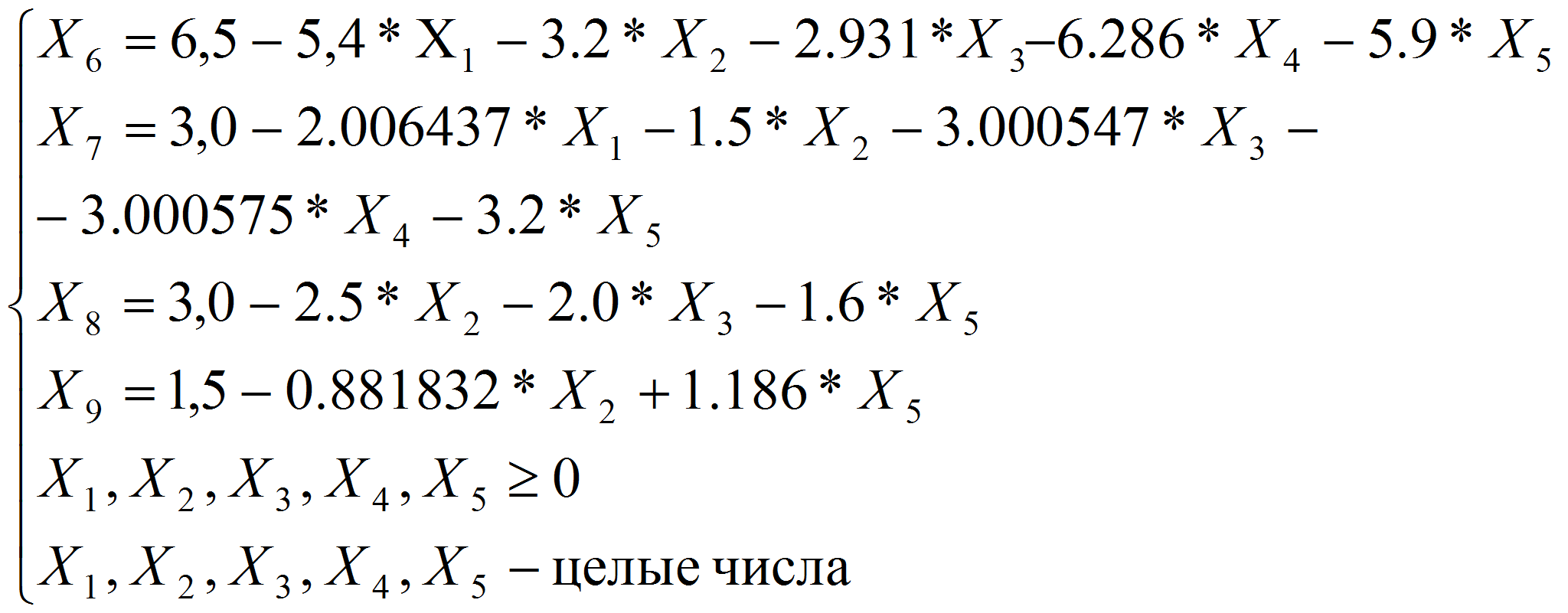Метод Гомори в решении целочисленной задачи оптимизации информационной системы

Целочисленное линейное программирование ориентировано на решение задач линейного программирования, в которых все или некоторые переменные принимают целочисленные значения [1, c. 136].

Для решения целочисленной задачи линейного программирования Р. Гомори предложил метод отсечения плоскостей в 1958 г. [1, c. 143].

Алгоритм Гомори содержит этапы:

Этап 1. Решение непрерывной задачи. Если решение дробное переход на 2 этап.

Этап 2. Решение расширенной задачи [2, c. 410].

Разработаем целочисленную математическую модель информационной системы и определим оптимальное решение методом Гомори.

Математическая модель формулируется следующим образом: из числа фирм, предоставляющих услуги спутникового Internet на территории Российской Федерации, требуется выбрать провайдера спутникового Internet с максимальной величиной чистого приведенного эффекта (NPV) и удовлетворяющих финансовым ограничениям [3, c. 58].

Пусть — доля финансирования проекта “НТВ-Плюс”, — доля финансирования проекта Europe On Line, — доля финансирования проекта Astra Network, — доля финансирования проекта Satpro, — доля финансирования проекта Network Service.

Целочисленная математическая модель имеет вид

при ограничениях (1)

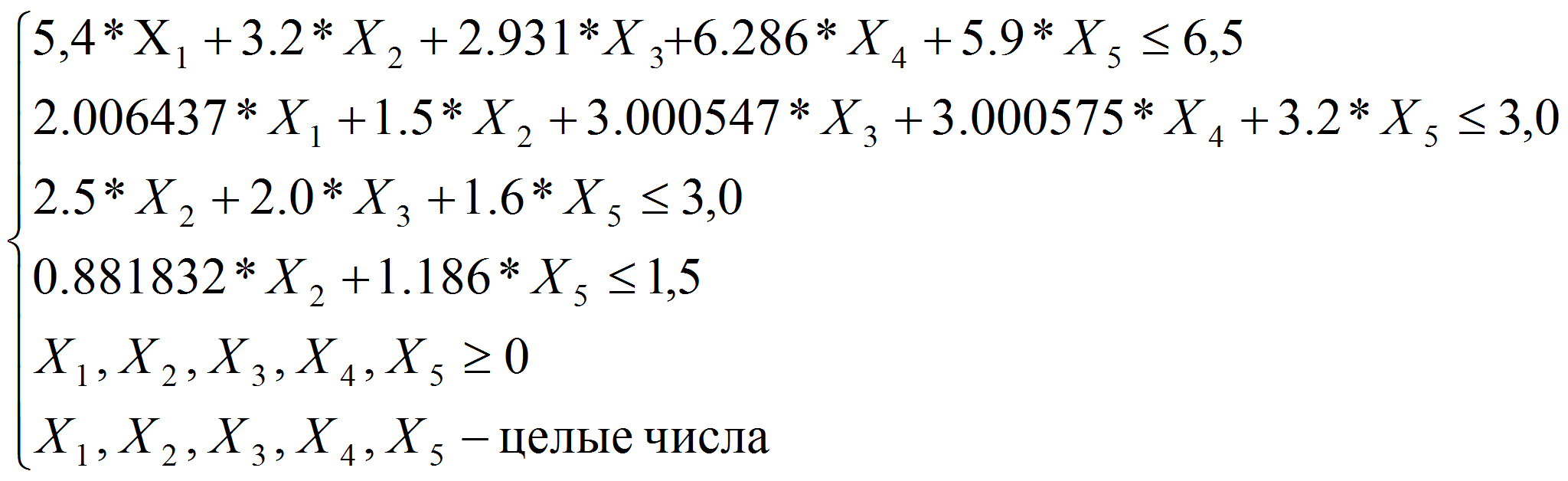Решим непрерывную задачу. Приведем к стандартной форме и составим исходную Жорданову таблицу (табл. 1).

при ограничениях (4)

(2)

Таблица 1

Начальная Жорданова таблица

В табл.2 приведена первая итерация.

Таблица 2

Первая итерация

В табл.3 приведено оптимальное решение непрерывной задачи.

Переход ко второму этапу алгоритма Гомори.

Выбирается базисная переменная с наибольшей дробной частью: , , . Для переменной составляется уравнение.

В табл. 4 и табл. 5 представлены расширенная задача и 3 итерация.

Таблица 3

Оптимальное решение непрерывной задачи. Вторая итерация

Таблица 4

Расширенная задача с первым дополнительным ограничением

Таблица 5

Третья итерация

В табл.6 приведено оптимальное нецелочисленное решение.

В табл.7 представлена расширенная задача со вторым дополнительным ограничением.

Таблица 6

Оптимальное нецелочисленное решение

Таблица 7

Расширенная задача со вторым дополнительным ограничением

В табл.8 приведена четвертая итерация. В табл.9 и табл.10 представлены расширенная задача и оптимальное целочисленное решение. Оптимальный целочисленный план = (табл. 10). Значение целевой функции Z=1.52728.

Результаты проведенных исследований позволили сделать следующие выводы.

1. Разработана целочисленная математическая модель оптимизации информационных систем, позволяющая сократить затраты и сроки проектирования информационных систем и повысить обоснованность принимаемых решений.

2. Найдено оптимальное решение целочисленной задачи оптимизации информационной системы методом Гомори.

Таблица 8

Четвертая итерация. Отсечение дробной части переменной

Таблица 9

Расширенная задача с третьим дополнительным ограничением

Таблица 10

Оптимальное целочисленное решение

Литература:

1. Таха Х. А. Введение в исследование операций. 7-е издание.: Пер. с англ. М.: Издательский дом “Вильямс”, 2005–912 c.

2. Конюховский П. В. Математические методы исследования операций в экономике. — СПб.: Издательство «Питер», 2000. — 208 с.

3. Семахин А. М. Анализ математической модели информационной системы. В сб. материалов X Всероссийской научно-практической конференции с международным участием (25–26 ноября 2011 г.). — Томск: Изд-во Том.ун-та, 2011. — Ч.2–206 с.