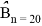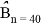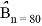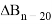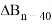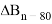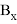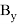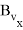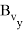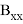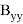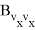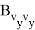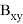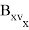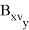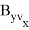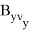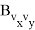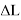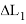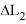В современных беспилотных баллистических летательных аппаратах межконтинентальной дальности полета в системе управления реализован функциональный метод наведения, определяющий правило выбора момента отключения разгонного блока в целях минимизации отклонения точки падения полезной нагрузки от точки прицеливания. Для реализации этого правила в состав полетного задания вводятся значения так называемых баллистических производных, которые определяются перед пуском летательного аппарата на основании расчетов программной траектории.
В работе раскрыт математический и физический смысл баллистических производных, рассмотрены методы их расчета средствами математического и регрессионного анализа.
Введение
Для простоты предположим, что полет летательного аппарата после отключения разгонного блока осуществляется только под действием однородного гравитационного поля, характеризуемого вектором

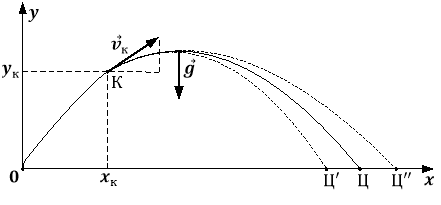
Рис. 1
Предположим, что точка прицеливания Ц лежит на оси
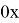
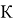
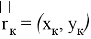
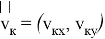
Если полет аппарата при работающем разгонном блоке осуществляется строго по рассчитанной программной траектории, то в момент его отключения центр масс аппарата окажется точно в точке с координатами
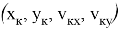
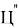
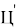
Для обеспечения точного попадания в цель в рамках реализации функционального наведения вместо фиксированного момента времени отключения разгонного блока используется момент, сформированный на основе анализа текущих параметров движения летательного аппарата. Такой анализ основан на расчете в процессе полета значения функции промаха
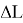
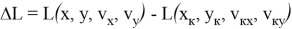
Разгонный блок необходимо отключить в тот момент, когда выполняется условие попадания в точку прицеливания, то есть в тот момент, когда функция промаха примет нулевое значение
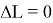
На практике реализация в системе управления летательным аппаратом алгоритма (1) вызывает большие трудности в силу вычислительной сложности. Поэтому вместо формулы (1) используется выражение на основе так называемого функционала управления дальностью.
Функционал управления дальностью получается в результате разложения в ряд Тейлора функции промаха
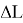
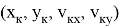
Введем обозначение для дифференциального оператора
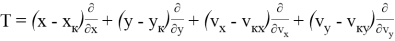
С учетом обозначения (3) разложение функции
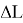
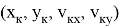
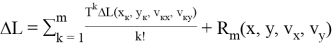
где
Ограничиваясь в (4) одним слагаемым
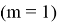
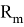
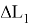
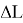
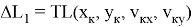
В случае использования двух слагаемых (
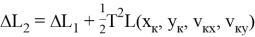
Выражения (5) и (6) обычно записываются в виде (7) и (8) соответственно
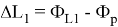
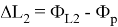
Второе слагаемое
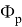
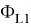
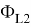
Настроечное значение
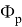
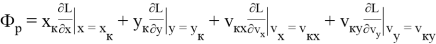
Значения частных производных в расчетной точке
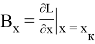
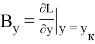
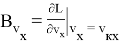
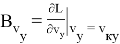
называются баллистическими производными. Каждая баллистическая производная показывает, насколько изменится дальность полета при отклонении соответствующего параметра движения на единицу.
Линейный функционал в обозначениях (10) принимает вид
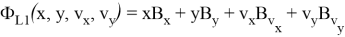
Таким образом, отключение разгонного блока может быть осуществлено в соответствии с правилом
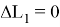
Реализация правила (12) предполагает вычисление перед стартом баллистических производных в расчетной точке фазового пространства и настроечного значения, а во время полета определение текущих параметров движения и вычисление линейного функционала.
Для реализации в системе управления квадратичного функционала необходим, в соответствии с выражением (6), дополнительный расчет баллистических производных высших порядков:
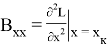
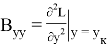
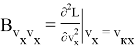
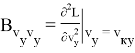
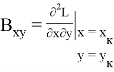
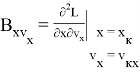
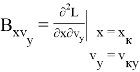
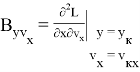
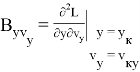
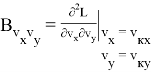
Квадратичный функционал в обозначениях (10) и (13) запишется как
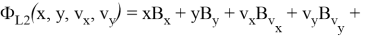
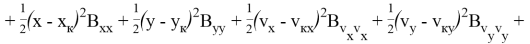
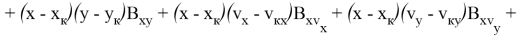
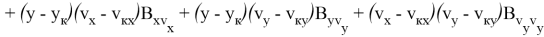
Отключение разгонного блока в данном случае выполняется в соответствии с правилом
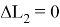
При известной расчетной точке
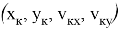
1) Рассчитать баллистические производные
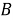
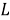
2) Рассчитать оценки баллистических производных
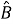
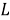
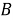
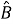
3) Сравнить точность аппроксимации функции промаха
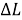
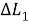
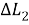
В рамках решения первой задачи для расчета аналитического выражения функции дальности
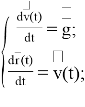
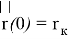
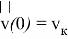
В результате решения (16) определим траекторию движения центра масс
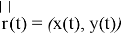
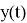
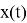
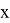
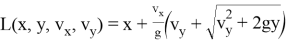
Зафиксировав расчетную точку в фазовом пространстве, вычисление баллистических производных по формулам (10), (13) не представляет особого труда. В дальнейшем размерности величин будем предполагать выраженными в системе СИ. Зададимся значением расчетной точки
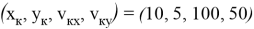
Баллистические коэффициенты, в этом случае, будут иметь значения, указанные в столбце «
Для решения второй задачи предположим, что зависимость величины промаха от отклонения фактической точки отключения разгонного блока описывается регрессионной моделью в каждом
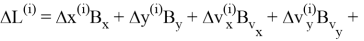
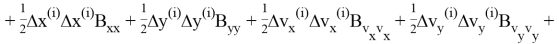
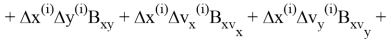
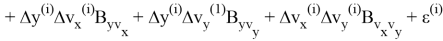
Здесь для некоторых символов
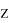
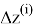
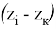
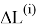
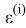
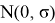
Для
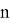
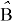
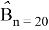
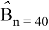
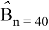
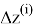
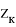
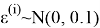
Таблица 1
|
|
|
|
|
|
|
|
|
|
|
1.0000 |
1.6835 |
0.9699 |
1.0023 |
-0,6835 |
0,0300 |
0,0023 |
|
|
1.9619 |
2.9871 |
2.0412 |
1.9049 |
-1,0253 |
-0,0793 |
-0,0570 |
|
|
10.3031 |
10.2681 |
10.3027 |
10.3025 |
0,0349 |
0,0003 |
-0,0006 |
|
|
20.2139 |
20.0919 |
20.2175 |
20.2084 |
0,1220 |
-0,0036 |
-0,0055 |
|
|
0.0000 |
-0.3232 |
0.7329 |
0.5460 |
0,3232 |
-0,7329 |
0,5460 |
|
|
-0.0074 |
3.2877 |
3.7573 |
0.8276 |
-3,2952 |
-3,7647 |
0,8350 |
|
|
0.0000 |
0.0052 |
-0.0013 |
0.0000 |
-0,0053 |
0,0013 |
0,0001 |
|
|
0.0076 |
0.1914 |
-0.0071 |
0.0087 |
-0,1839 |
0,0147 |
0,0012 |
|
|
0.0000 |
-5.6646 |
0.3972 |
-0.3288 |
5,6646 |
-0,3972 |
-0,3288 |
|
|
0.0000 |
0.0297 |
-0.0009 |
-0.0072 |
-0,0297 |
0,0009 |
-0,0072 |
|
|
0.0000 |
0.7074 |
-0.0020 |
-0.0099 |
-0,7074 |
0,0020 |
0,0099 |
|
|
0.0196 |
0.1881 |
0.0127 |
0.0024 |
-0,1686 |
0,0068 |
-0,0172 |
|
|
-0.0378 |
0.3402 |
-0.0510 |
-0.0255 |
-0,3780 |
0,0132 |
0,0123 |
|
|
0.2021 |
0.1641 |
0.1985 |
0.2008 |
0,0379 |
0,0035 |
-0,0013 |
Отклонения
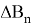
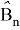
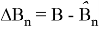
представлены в колонках «
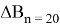
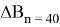
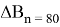
В рамках решения третьей задачи зафиксируем значение отклонения точки фактического отключения разгонного блока от расчетного
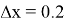
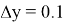
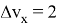
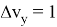
и определим величины истинного промаха и величины промахов, рассчитанных на основании линейной и квадратичной аппроксимации при различном объеме измерений. Результаты расчетов сведены в таблицу 2.
Таблица 2
|
|
|
|
|
|
|
41.6245 |
41.2163 |
41.6245 |
|
|
41.6245 |
41.2635 |
41.8195 |
|
|
41.6245 |
41.2210 |
41.6499 |
|
|
41.6245 |
41.2044 |
41.6119 |
Данные в таблице сформированы на основе теоретических и оценочных значений баллистических коэффициентов, рассчитанных на основе выборочных данных различного объема (
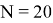
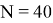
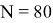
На основе полученных данных можно предположить, что с увеличением объема измерений точность определения баллистических коэффициентов будет возрастать, что приведет к более точной линейной и квадратичной аппроксимации функции промаха.
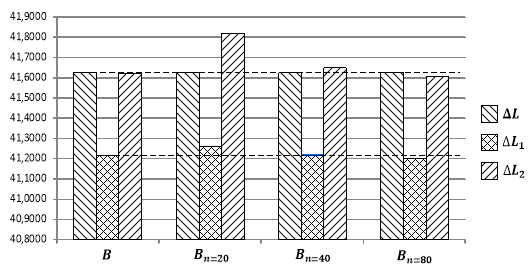
Рисунок 2
Кроме того, из рисунка 2 видно, что квадратичная аппроксимация существенно точней описывает функцию промаха по сравнению с линейной для любого рассмотренного объема измерений.
Заключение
Решение поставленных задач позволило оценить точность замены теоретической функции промаха ее линейным и квадратичным приближением при известных теоретических значениях баллистических производных. В силу того, что расчет баллистических производных на практике не может быть выполнен методами математического анализа из-за невозможности определения функции дальности в аналитическом виде, показана возможность их определения методами регрессионного анализа на основе данных об испытательных пусках. При этом испытательные пуски могут быть смоделированы на ЭВМ. Полученные оценки баллистических коэффициентов позволяют построить достаточно точную аппроксимацию теоретической функции промаха.
Литература:
- Разоренов, Г. Н. Системы управления летательными аппаратами: учебник для вузов / Ю. Ф. Титов, Э. А. Бахрамов, Г. Н. Разоренов. — М.: Машиностроение, 2003. 586 с.
- Жанжеров, Е. Г. Системы управления движением летательных аппаратов: конспект лекций. Ч. 1. / Е. Г. Жанжеров. — Пермь: ПВВКИУ, 1995. 75 с.
- Дрейпер, Н. Прикладной регрессионный анализ. Кн. 1 / Н. Дрейпер, Г. Смит; Пер. с англ. Ю. П. Адлер, В. Г. Горский. — М.: Финансы и статистика, 1986. — 366 с.