В статье рассматриваем теорему о непрерывных изображениях, также рассматривается лемма о непрерывных операторах и получены к ним доказательства. Дано определение нелинейному оператору.
Ключевые слова: банаховы пространства, непрерывный оператор, компактность.
До сравнительно недавнего времени теория нелинейных уравнений представляла собой набор разрозненных результатов, касающихся отдельных задач. Однако за последние годы были достигнуты большие успехи, и сейчас в нашем распоряжении имеются довольно общие результаты о нескольких широких классах уравнений. Важную роль в этом процессе сыграл функциональный анализ. Пожалуй, именно здесь вклад функционально-аналитических методов в приложения оказался наиболее ценным. При изучении линейных операторов в банаховых пространствах большую помощь при отыскании путей исследования оказывают весьма содержательные общие принципы, известные для конечномерного случая. Почти все трудности связаны здесь исключительно с переходом от конечного числа измерений к бесконечному и потому носят, по существу, аналитический характер. В случае нелинейных операторов тоже естественно обратиться сначала к конечномерным аналогиям. Однако конечномерные нелинейные задачи часто и сами очень сложны. Изучением таких задач активно занимаются и в настоящее время, причём многие из основных результатов в этой области получены лишь недавно; стандартное руководство по конечномерным нелинейным задачам — книга Ортеги и Рейнболдта. Теорию нелинейных операторов в конечномерном случае можно классифицировать как геометрическую теорию, ибо в ней исследуют «форму» функций. Поэтому можно сказать, что теория нелинейных операторов в банаховых пространствах состоит из геометрической и аналитической частей и что геометрическая часть играет более заметную роль, чем в линейной теории.
Определение 1.
Нелинейный оператор — это отображение А, пространство
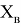
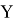
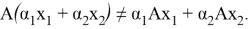
Теорема 1.
Пусть
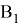
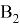
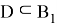
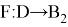
Это некоторое изображение. Тогда следующие два условия эквиваленты:
1)
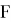
2) Для каждого
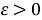
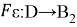
Что
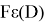
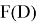
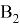
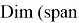
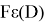
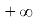
и
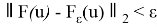
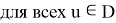
Доказательство 1.
В силу ограниченности
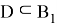
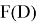
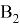

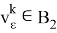
При
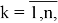
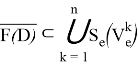
Где
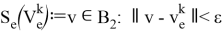
Введем следующие функции
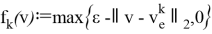
И рассмотрим следующую функцию
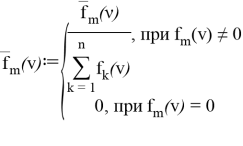
При
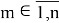
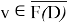
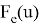
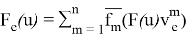
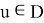
Ограниченность этого отображения для каждого фиксированного ε > 0 очевидна. Докажем непрерывность. По своему построению
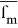
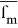
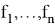
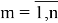
непрерывна по совокупности вещественных переменных
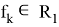
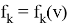
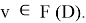
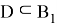
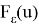
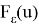
span
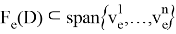
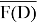
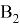
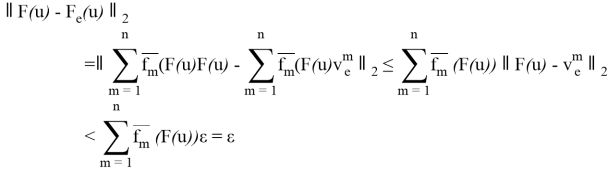
Пусть
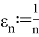
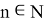
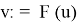
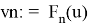
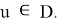
С одной стороны,
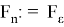
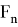
Действительно, для любого ε > 0 в силу непрерывности отображения
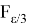
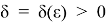
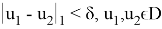
имеет место неравенство
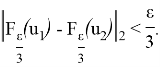
Таким образом, приходим к неравенству
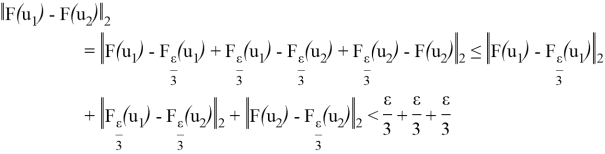
С другой стороны, имеет место следующее неравенство:
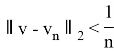
но множество
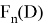
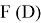
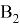
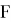
Пока рассмотрели связь полной непрерывности и вполне непрерывности линейных операторов. Однако, есть некоторые результаты и для нелинейных операторов. Справедлива следующая лемма [1–8].
Лемма 1. Пусть
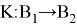
это полностью непрерывный оператор. Тогда при условии рефлексивности банахова пространства B1 оператор K является вполне непрерывным.
Доказательство 2. Пусть
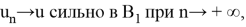
Но тогда, очевидно,
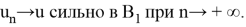
Отсюда в силу полной непрерывности оператора K приходим к выводу, что
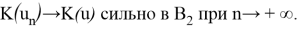
Тем самым, непрерывность оператора
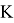
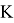
Действительно, пусть
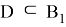
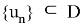
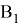
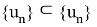
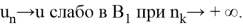
Поэтому в силу полной непрерывности оператора K приходим к выводу, что
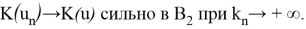
Теорема 2.
Пусть
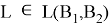
Доказательство 3. Пусть
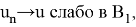
тогда эта последовательность ограничена в
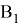
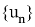
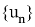
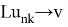
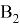
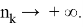
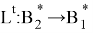
Поскольку
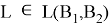
и
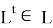
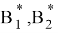
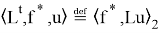
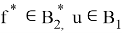
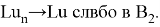
Действительно, имеет место следующее выражение:
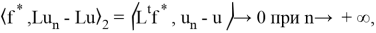
Поскольку
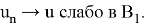
Таким образом, приходим к выводу, что
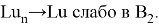
Докажем теперь, что на самом деле
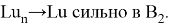
По доказанному,
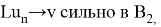
значит,
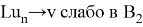
Следовательно, приходим к равенству
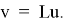
Теперь предположим, что найдется такая под последовательность
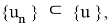
что имеет место неравенство
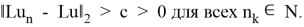
С другой стороны, по доказанному, у этой под последовательности
найдется такая под последовательность
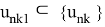
такая, что
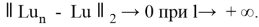
Справедлива цепочка неравенств
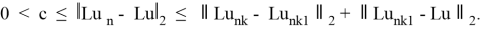
Выберем теперь l ∈ N настолько большим, чтобы имело место неравенство
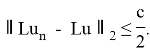
С другой стороны, для каждого
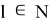
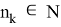
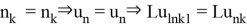
и тогда
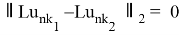
и приходим к неравенству
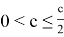
Полученное противоречие доказывает теорему.
Литература:
- Забрейко П. П. Идеальные пространства функций. — Качественные и приближенные методы исследования операторных уравнений // Вестник Ярославского университета. Вып. 8. Ярославль, 1974. С. 12–52.
- Ахмеров Р. Р., Каменский М. И., Потапов А. С. и др. Меры некомпактности и уплотняющие операторы. — Новосибирск: Наука, 1986.
- Yerzakova N. A. On Measures of Non-Compactness in Regular Spaces// Zeitschrift főr Analysis und ihre Anwendendungen. 1996.V. 15. № 2, р. 299–307.
- Ерзакова Н. А. Компактность по мере и мера некомпактности // Сиб. Мат.Ж. 1997. Т. 38, № 5. С. 1071- 1073.
- Ерзакова Н. А. Нелинейное уравнение и весовое неравенство // Современные проблемы функционального анализа и дифференциальных уравнений: Труды конференции ВГУ, 2003. С. 77–81.
- Красносельский М. А., Забрейко П. П. Геометрические методы нелинейного анализа. — М.: Наука, 1975.
- Красносельский М. А., Забрейко П. П. и др. Интегральные операторы в пространствах суммируемых функций. — М.: Наука, 1966.
- Kalton N. J., Verbitsky I. E. Nonlinear equations and weighted norm inequalities// Trans. Amer. Math. Soc. 1999. V. 351. № 9, р. 3441–3497.







