Рассматривается система однородных линейных рекуррентных соотношений первого порядка, записанная в векторном виде. Оператор в правой части системы действует в пространстве ![]() . Исследуются следующие случаи его собственных значений: 1) вещественные, единичной алгебраической кратности; 2) кратные вещественные; 3) комплексно сопряженные. Получено общее решение в аналитическом виде. Результаты иллюстрируются примерами с конкретными операторами.
. Исследуются следующие случаи его собственных значений: 1) вещественные, единичной алгебраической кратности; 2) кратные вещественные; 3) комплексно сопряженные. Получено общее решение в аналитическом виде. Результаты иллюстрируются примерами с конкретными операторами.
Ключевые слова: система линейных рекуррентных соотношений, первый порядок, общее решение.
Рассматривается система линейных рекуррентных соотношений (далее, ЛРС) первого порядка, записанная в векторном виде:
![]() (1)
(1)
где ![]() — искомая вектор-последовательность,
— искомая вектор-последовательность, ![]() — оператор, задаваемый числовой квадратной матрицей,
— оператор, задаваемый числовой квадратной матрицей, ![]() .
.
Системами рекуррентных соотношений задаются модели, описывающие развитие (идеализированной) популяции кроликов [1], распределение государством денежной массы по агрегатам [2], взаимодействие с окружающей средой (например, вырубка лесов) [3] и т. д.
Приведем необходимые для решения задачи сведения [4].
Определение 1. Собственное значение ![]() оператора
оператора ![]() — это корень характеристического уравнения
— это корень характеристического уравнения
![]() (2)
(2)
где
Определение 2. Собственный вектор ![]() , отвечающий собственному значению
, отвечающий собственному значению ![]() , определяется при решении уравнения
, определяется при решении уравнения
![]() (3)
(3)
Определение 3. Алгебраической кратностью собственного значения ![]() назовем степень соответствующего множителя
назовем степень соответствующего множителя ![]() , с которым он входит в разложение характеристического уравнения.
, с которым он входит в разложение характеристического уравнения.
В настоящей работе будет построено решение ЛРС (1) в следующих случаях: I) вещественных, единичной алгебраической кратности, II) кратных вещественных, III) комплексных собственных значений оператора ![]() .
.
- Случай I
Исследуется случай: оператор ![]() имеет собственные значения единичной алгебраической кратности. Пусть
имеет собственные значения единичной алгебраической кратности. Пусть ![]() ,
, ![]() ,
, ![]() ,
, ![]() ‒ собственные значения оператора
‒ собственные значения оператора ![]() , а
, а ![]() ,
, ![]() ,
, ![]() ,
, ![]() ‒ собственные векторы, отвечающие этим собственным значениям.
‒ собственные векторы, отвечающие этим собственным значениям.
Имеет место следующее утверждение.
Лемма 1. Пусть ![]() ‒ собственное значение оператора
‒ собственное значение оператора ![]() , а
, а ![]() — собственный вектор, отвечающий этому собственному значению. Тогда последовательность
— собственный вектор, отвечающий этому собственному значению. Тогда последовательность
![]() (4)
(4)
является частным решением соотношения (1).
Доказательство. Действительно, подставив последовательность (4) в соотношение (1) вместо ![]() , получим:
, получим:
![]()
Последнее равенство верно в силу определения 2. Лемма доказана.
Из леммы 1 вытекает следующий результат.
Теорема 1. Последовательность
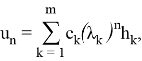
где ![]() ‒ произвольные скаляры, является общим решением соотношения (1).
‒ произвольные скаляры, является общим решением соотношения (1).
- Случай II
Исследуется случай: оператор ![]() имеет кратные собственные значения. Пусть собственное значение
имеет кратные собственные значения. Пусть собственное значение ![]() имеет алгебраическую кратность
имеет алгебраическую кратность ![]() .
.
Рассмотрим вспомогательное дифференциальное уравнение:
![]() (5)
(5)
Частное решение этого уравнения, отвечающее собственному значению ![]() , равно
, равно
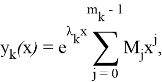
где здесь и далее ![]() — произвольные вектор-постоянные [5].
— произвольные вектор-постоянные [5].
Определим функционал для непрерывно дифференцируемой ![]() раз в точке
раз в точке ![]() функции
функции ![]() формулой:
формулой:
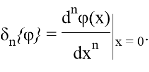
Имеет место следующее утверждение.
Лемма 2. Для всех ![]() имеет место равенство:
имеет место равенство:
![]()
где ![]() — количество размещений из
— количество размещений из ![]() элементов по
элементов по ![]() .
.
Доказательство. По формуле Лейбница имеем
![]() (6)
(6)
где ![]() — биномиальный коэффициент. Нетрудно видеть, что
— биномиальный коэффициент. Нетрудно видеть, что
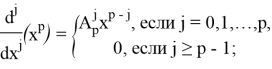
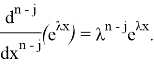
Подставив два последних равенства в (6), учитывая, что при ![]() слагаемые суммы равны нулю, получим:
слагаемые суммы равны нулю, получим:
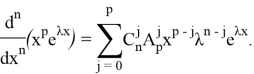
Выделим в сумме слагаемое с ![]() , имея
, имея ![]()
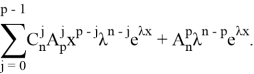
Взяв в последнем выражении ![]() , получим утверждение леммы. Лемма доказана.
, получим утверждение леммы. Лемма доказана.
Методом, введенным в работе [6], с применением леммы 2 получено следующее утверждение.
Лемма 3. Частное решение ЛРС (1), отвечающее собственному значению ![]() равно
равно
![]() (7)
(7)
Тем самым, справедлив следующий результат.
Теорема 2. Общее решение соотношения (1) является суммой частных решений (7):
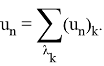
- Случай III
Пусть оператор ![]() имеет комплексно-сопряженные собственные значения вида
имеет комплексно-сопряженные собственные значения вида
![]() (8)
(8)
Частное решение ![]() уравнения (5), отвечающее собственному значению (8), раскладывается по собственным функциям
уравнения (5), отвечающее собственному значению (8), раскладывается по собственным функциям ![]() ,
, ![]() [5]:
[5]:
![]()
Имеет место следующий результат.
Лемма 4. Частное решение ![]() для ЛРС (1), отвечающее собственным значениям (8), определяется формулой:
для ЛРС (1), отвечающее собственным значениям (8), определяется формулой:
![]() (9)
(9)
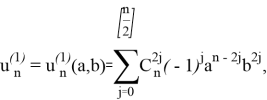
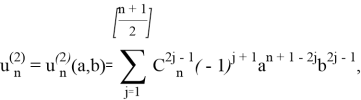
где
Доказательство. Применим тот же метод доказательства, что и в предыдущем пункте. Частное решение ![]() для ЛРС (1), отвечающее собственному значению (8), равно
для ЛРС (1), отвечающее собственному значению (8), равно
![]() (10)
(10)
По формуле Лейбница
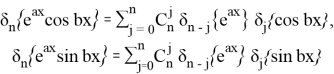 (11)
(11)
Далее, нетрудно видеть, что
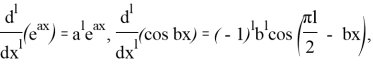
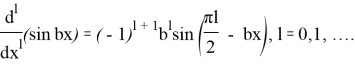
Взяв в последних соотношениях ![]() и подставив в (11), (10), в силу соотношений:
и подставив в (11), (10), в силу соотношений:
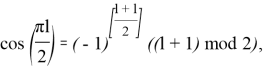
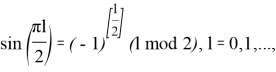
где символом mod обозначен остаток от деления, приходим к формуле из утверждения леммы. Лемма доказана.
Из леммы 4 вытекает следующий результат.
Теорема 3. Общее решение ![]() — это сумма частных решений, каждое из которых отвечает своей паре комплексно сопряженных собственных значений оператора
— это сумма частных решений, каждое из которых отвечает своей паре комплексно сопряженных собственных значений оператора ![]() . Эти частные решения определяются по формуле (9).
. Эти частные решения определяются по формуле (9).
- Примеры
Проиллюстрируем полученные результаты следующими примерами.
Пример 1. Решить следующую систему ЛРС
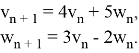 (12)
(12)
Система (12) — это система вида (1) с искомой вектор-последовательностью
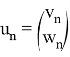
и оператором
![]()
1) Вычислим собственные числа оператора ![]() . Для этого решим характеристическое уравнение (2):
. Для этого решим характеристическое уравнение (2):
![]()
2) Вычислим собственные векторы ![]() ,
, ![]() , отвечающие собственным числам
, отвечающие собственным числам ![]() ,
, ![]() . Решив уравнение (3), получим:
. Решив уравнение (3), получим:
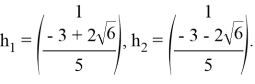
3) Оператор ![]() имеет вещественные собственные значения единичной алгебраической кратности, следовательно, имеет место случай I. Общее решение системы (12) в силу теоремы 1 равно
имеет вещественные собственные значения единичной алгебраической кратности, следовательно, имеет место случай I. Общее решение системы (12) в силу теоремы 1 равно
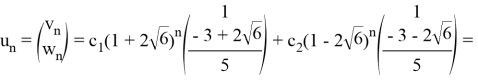
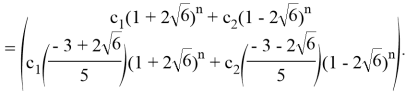
Непосредственной подстановкой последнего выражения в исходную систему убеждаемся в истинности решения.
Пример 2. Решить следующую систему ЛРС
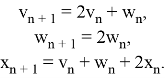 (13)
(13)
Система (13) — это система вида (1) с искомой вектор-последовательностью
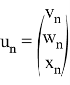
и оператором
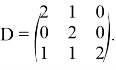
1) Вычислим собственные числа оператора ![]() . Для этого решим характеристическое уравнение:
. Для этого решим характеристическое уравнение:
![]()
![]()
2) Оператор ![]() имеет вещественное собственное значение алгебраической кратности 3, следовательно, имеет место случай II. Общее решение системы (13) в силу теоремы 2 равно
имеет вещественное собственное значение алгебраической кратности 3, следовательно, имеет место случай II. Общее решение системы (13) в силу теоремы 2 равно
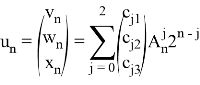
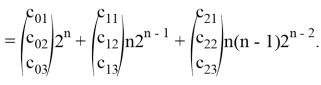
Чтобы выразить одни коэффициенты через другие, применим следующее утверждение [6].
Утверждение. Система последовательностей ![]() образует базис.
образует базис.
Из него вытекает следствие.
Следствие. Пусть ![]() — постоянные. Тогда равенство нулю линейной комбинации
— постоянные. Тогда равенство нулю линейной комбинации ![]() влечет равенство нулю ее коэффициентов.
влечет равенство нулю ее коэффициентов.
Подставив полученное выражение во второе соотношение системы, в силу следствия, получим:
![]()
Подстановка полученного выражения в третье соотношение системы влечет равенства:
![]()
Наконец, из первого соотношения системы получаем:
![]()
Взяв в качестве параметров ![]() ,
, ![]() ,
, ![]() ,
, ![]() , получим искомое решение системы:
, получим искомое решение системы:
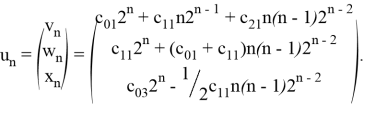
Пример 3. Решить следующую систему ЛРС
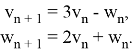 (14)
(14)
Система (14) — это система вида (1) с искомой вектор-последовательностью
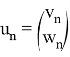
и оператором
![]()
1) Решив характеристическое уравнение
![]()
вычислим собственные числа оператора ![]() :
:
![]()
2) Оператор ![]() обладает комплексными собственными значениями, следовательно, имеет место случай III. Общее решение системы (14) в силу теоремы 3 равно
обладает комплексными собственными значениями, следовательно, имеет место случай III. Общее решение системы (14) в силу теоремы 3 равно
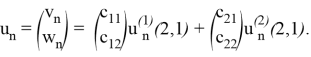 (15)
(15)
3) Для определения коэффициентов подставим (15) в (14), взяв
![]()
Таким образом,
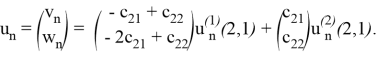
Некоторые результаты настоящей работы апробированы на конференции [7].
Литература:
- Неверова Г. П. Режимы динамики лимитированной структурированной популяции при избирательном промысле / Г. П. Неверова, А. И. Абакумов, Е. Я. Фрисман // Математическая биология и биоинформатика. 2017. Т. 12. № 2. С. 327–342.
2. Денежная масса и денежная база. Структура денежной массы [электронный ресурс]. Режим доступа: https://studopedia.ru/6_106532_denezhnaya-massa-i-denezhnaya-baza-struktura-denezhnoy-massi.html (дата обращения: 21.12.2019).
- Игнатенко В. В., Турлай И. В., Федоренчик А. С. Моделирование и оптимизация процессов лесозаготовок: учебное пособие для студентов специальности «Лесоинженерное дело». Мн.: БГТУ, 2004.
- Бирман М. Ш., Виленкин Н. Я., Горин Е. А. Функциональный анализ. М.: Наука. 1972. 544 с.
- Понтрягин Л. С. Обыкновенные дифференциальные уравнения. М.: Наука, 1974. 331 с.
- Усков В. И., Анжаурова Т. М. Решение линейных рекуррентных соотношений второго порядка // Молодой ученый. 2019. № 42 (280). C. 1–6.
- Бурчакова Т. Л., Довгаль В. А. Решение одной системы линейных рекуррентных соотношений первого порядка // Материалы VI Международной научно-практической конференции (школы-семинара) молодых ученых «Прикладная математика и информатика: современные исследования в области естественных и технических наук». Тольятти, 2020.







