The theory of solving inverse problems in mathematical physics is one of the most dynamically developing areas of modern mathematics. The increased interest of researchers in such problems is primarily due to the rapidly growing number of applications that have emerged in recent years amid the rapid advances in physics and technology. Despite the existence of numerous methods for solving inverse problems, the need to develop new approaches that account for the ill-posedness of many of them remains high. The inverse problem of determining a time-dependent source in a parabolic equation is being studied.

Keywords: parabolic equation, inverse problem, nonlocal problem, loaded equation.

Введение

Обратным задачам математической физики, включая аналитические и численные методы их решения, в частности начально-краевым задачам для параболических уравнений, посвящено значительное число исследований. Существенный интерес у специалистов, разрабатывающих численные методы для обратных и некорректных задач параболического типа, вызывают градиентные методы [1], прежде всего метод наискорейшего спуска [2]. К числу значимых работ, рассматривающих анализ и решение задач восстановления граничных условий для уравнений параболического типа, относятся публикации [1–4]. Вместе с тем до настоящего времени сохраняется актуальность разработки эффективных численных методов решения граничных обратных задач для уравнений теплопроводности. Численное решение обратной задачи для параболического уравнения с нелинейным коэффициентом проводимости представляет собой сложную задачу идентификации неизвестных параметров, таких как коэффициент теплопроводности.

Постановка задачи . Рассмотрим начально-краевую задачу для нелинейного уравнения тепопроводности:

(1)

(2)

(3)

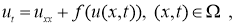
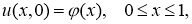
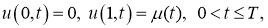
где функции будем считать заданными.

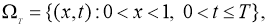
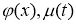
Обратная задача . Пусть . Требуется найти пару функций из условий (1)-(3) по следующей дополнительной информации

(4)

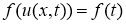
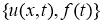
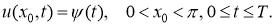
Предположим, что начальные и граничные условия согласованы:

(5)

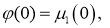
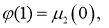
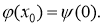
Определение 2. Пара функций и называется решением обратной задачи (1)-(4), если , и удовлетворяют равенствам (1)-(4) в классическом смысле.

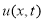
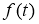
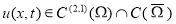
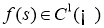
Сначала изучим прямую задачу (1)-(3).

Докажем, что при этих предположениях существование решения задачи (1)-(3) доказывается сведением ее к интегральному уравнению.

Справедлива

Теорема 1. Пусть функции , удовлетворяют следующим условиям , , .Тогда начально-краевая задача (1)-(3) имеет единственное решение и .

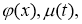
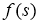
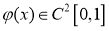
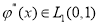
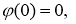
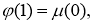
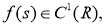
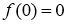
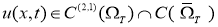
Доказательство. Пусть функция Грина первой начально краевой задачи для уравнения теплопроводности. Тогда решение задачи (1) -(3) эквивалентным образом сводится к интегральному уравнению второго рода

(6)

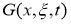
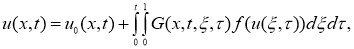
где

(7)

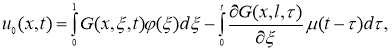
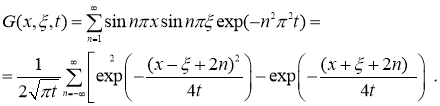
Покажем, что уравнение (6) определяет единственное непрерывное в области решение. Для этого воспользуемся методом последовательных приближений, представив в виде ряда

(8)

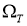
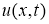
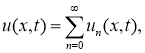
где находятся по формулам:

(9)

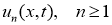
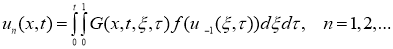
Из условий теоремы следует, что . Используя метод математической индукции, нетрудно показать, что

(10)

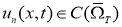
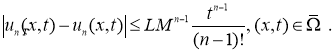
Докажем единственность решения уравнения (8). Пусть функции есть два решения уравнения (8). Тогда для их разности

справедлива

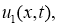
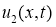
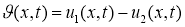
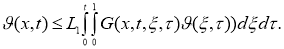
Введем обозначение

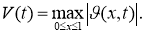
Тогда из последнего неравенства следует

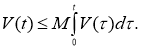
Следовательно, при и в и теорема 1 доказана.

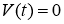
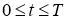
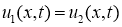
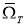
2. Сведение обратной задачи к начально-краевой задаче для нагруженного уравнения.

Переходим к исследованию обратной задачи (1) -(4). Положив в (1) и используя (4), получим

(11)

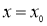
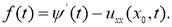
Постановка (11) в (1) дает искомое нагруженное уравнение

(12)

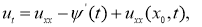
Таким образом, получили линейное нагруженное уравнение для уравнение теплопроводности.

Рассмотрим начально-краевую задачу (12), (2),(3). Из этой задачи, имеем

(6)

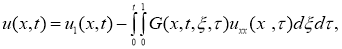
где

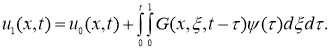
Продифференцировав (1.6) два раза по переменной х и положив , получим

(7)

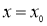
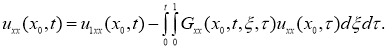
Равенства (1.6), (1.7) определяют систему линейных интегральных уравнений типа Вольтерра второго рода относительно функций и .

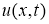
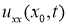
Решая эту систему уравнений, например методом сжимающих отображений, находим функции и . А по формуле (11) однозначно находим функцию .

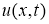
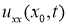
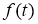
3. Сведение обратной адачи (1) -(4) к нелокальной задаче.

Введем функцию

(13)

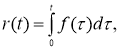
Тогда функция

(14)

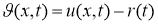
Будет удовлетворят задаче

(15)

(16)

(17)

(18)

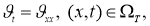
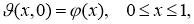
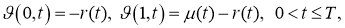
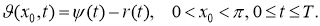
Учитывая (17), (18) из задачи (15) -(18), получим

(19)

(20)

(21)

(22)

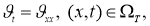
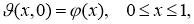
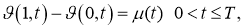
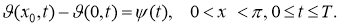
Решив задачу (19) -(22), например методом Фурье находим функций

и , затем по формуле (14) функцию .

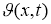
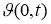
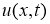
Пример 1.

(23)

(24)

(25)

(26)

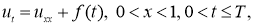
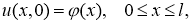
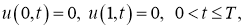
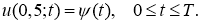
Эта задача имеет точное решение

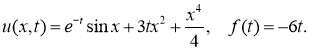
Литература:

1. Алифанов О. М. Обратные задачи теплообмена. М.: Машиностроение, 1988. — 280 с.

2. Beck J. V., Blackwell B., St. Clair C. R., Jr. Inverse Heat Conduction. I11-posed Problems. A Wiley-Interscience Publication, New York, 1985, 308 p.

3. Самарский А. А., Вабищевич П. Н. Численные методы решения обратных задач. — М.: ЛКИ, 2007. — 480 с.

4. Hao D. Methods for inverse heat conduction problems. — Peter Lang pub. Inc. 1998. — 249 p.