В данной работе исследуется нелинейная обратная задача определения коэффициента для линейного уравнения теплопроводности с дробными по времени производными с условием переопределения во внутренней точке. Методом Фурье эта обратная задача сводится к эквивалентной системе нелинейных интегральных уравнений. Затем, используя оценки функции Миттаг-Леффлера и некоторые ее свойства, обратная задача сводится к эквивалентной системе нелинейных интегральных уравнений типа Вольтерра второго рода. Для решения этой системы применяется метод операторных уравнений Вольтерра. Доказаны локальные теоремы существования и единственности в целом решения рассматриваемой обратной задачи.
Ключевые слова: уравнение дробного по времени порядка, дробная производная обратная задача, интегральное уравнение·Вольтерра.
In this paper, we study the nonlinear inverse problem of determining the coefficient for a linear heat conduction equation with fractional time derivatives with an overdetermination condition at an interior point. Using the Fourier method, this inverse problem is reduced to an equivalent system of nonlinear integral equations. Then, using estimates of the Mittag-Leffler function and some of its properties, the inverse problem is reduced to an equivalent system of nonlinear integral equations of the Volterra type of the second kind. To solve this system, the Volterra operator equation method is used. Local theorems of existence and uniqueness are proved for the entire solution of the inverse problem under consideration.
Keywords: Fractional time equation, Fractional derivative, Inverse problem, Integral equation, Volterra.
Введение
В последние годы дробное исчисление привлекает широкое внимание и успешно применяется к различным отраслям науки, таких как биологии [1], физике [2], химии и биохимии [5], гидрологии [6], медицине [7,8] и финансах [9,10]. Уравнения дробной диффузии по времени выводятся путем замены стандартной производной по времени на дробную производную по времени и могут использоваться для описания явлений супердиффузии и субдиффузии [11–13]. Прямые задачи для уравнений дробной диффузии по времени широко изучались в последние годы [14–17].
В последнее время исследование дробных дифференциальных уравнений достигло большого прогресса. В литературе существует несколько определений дробных интегралов и производных, наиболее популярные определения — в смысле производных Римана–Лиувилля и Капуто.
Уравнение с дробными производными по времени было получено путем замены классической производной по времени на дробную производную по времени. Прямые задачи, такие как задачи Коши и начально-краевые задачи для уравнения с дробными производными по времени, широко изучались в последние годы (см. [10–16]).
Прямые и обратные задачи для псевдопараболического уравнения третьего порядка с дробными производными изучались в работах (см. [17–21]).
Обратные задачи для целочисленных и дробных уравнений в частных производных — бурно развивающаяся область математики. Если классические постановки краевых задач для этих уравнений уже достаточно хорошо изучены и получены условия их разрешимости, то с обратными задачами дело обстоит сложнее. Зачастую даже сама постановка таких задач требует дополнительных исследований, в том числе и изучения дифференциальных свойств решений прямых задач.
- Некоторые сведения в дробном исчислении.
Введем некоторые понятия, необходимые для дальнейшего исследования [10–17].
Определение 1.
Дробным дифференциальным оператором Капуто
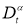
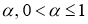
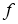
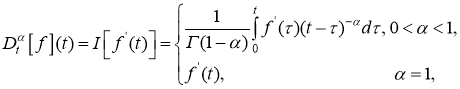
где
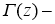
Определение 2.
Дробным интегральным оператором Римана-Лиувилля
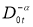
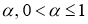
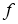
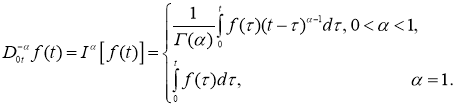
Определение 3.
Дву параметрическая функция
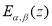
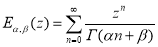
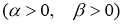
называется функцией Миттаг-Леффлера.
Приведем некоторые соотношения, приведенные в [3]- [6]:
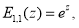
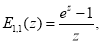
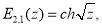
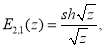
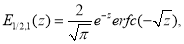
При
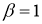
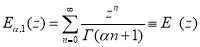
Обобщение формулы Ньютона-Лейбница, при
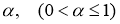
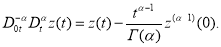
Рассмотрим следующую задачу Коши для линейного обыкновенного дифференциального уравнения с дробными производным порядка
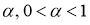
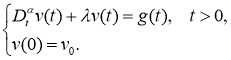
Приводим результат существование и единственность решения рассматриваемой задачи, которые приведены в [15].
Лемма 1.
Пусть
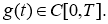
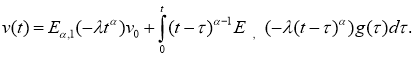
Лемма 2.
Пусть
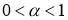
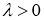
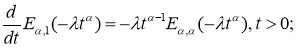
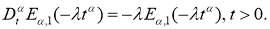
Лемма 2.
Пусть
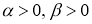
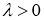
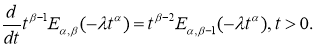
Лемма 3
(см. [12]). Если для
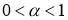
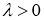
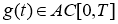
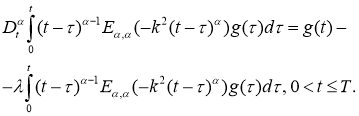
В частности, если
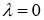
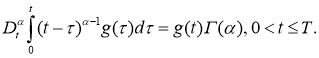
Пусть
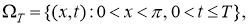
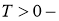
2.Постановка и
исследование обратной задачи.
Вобласти
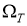
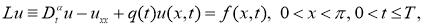
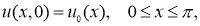
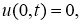
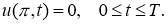
где
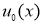
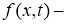
Здесь
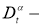
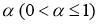
Обратная задача
.
Требуется найти пару функций
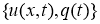
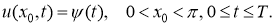
Пусть все заданные функции достаточно гладкие
Определение 3.
Функция
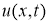
1. 1)
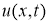
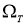
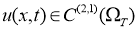
2. 2) удовлетворяет уравнению (16), начальному условию (17) и граничным условиям (18) в классическом смысле.
Определение 4.
Пара функций
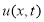
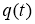
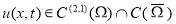
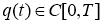
Справедлива
Теорема 1.
Пусть
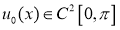
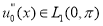
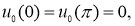
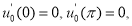
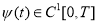
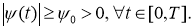
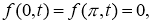
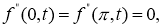
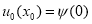
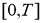
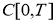
Доказательство.
Пусть
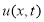
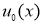
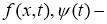
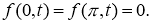
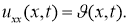
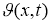
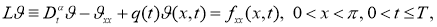
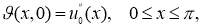
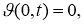
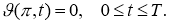
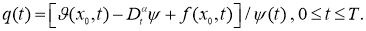
Заменим теперь задачу (2.5) -(2.7) эквивалентным ей интегральным уравнением
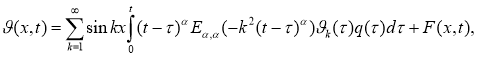
где
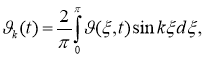
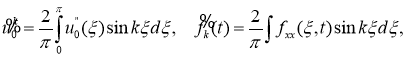
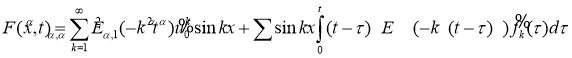
Положив в (2.9)
х
=
х
0
, получим выражение для
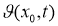
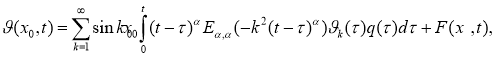
Подставляя (25) в(23), получим
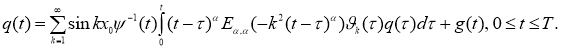
где
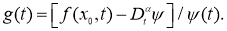
Равенства (24), (26) определяют систему нелинейных интегральных уравнений типа Вольтерра второго рода относительно функций
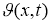
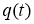
Решая эту систему уравнений при малом
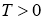
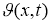
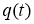
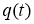
Литература:
- Yuste S., Lindenberg, K. Subdiffusion-limited reactions, Chem. Phys. 284 (1) (2002) 169–180.
- Metzler, R. Klafter, J.Boundary value problems for fractional diffusion equations, Physica A 278 (1) (20 0 0) 107–125.
- Metzler, R., Klafter, J. The random walk’s guide to anomalous diffusion: a fractional dynamics approach, Phys. Rep. 339 (1) (20 0 0) 1–77.
- Saichev, A., Zaslavsky, G. Fractional kinetic equations: solutions and applications, Chaos 7 (4) (1997) 753–764.
- Yuste, S. Acedo, L.,Lindenberg K., Reaction front in an A + B → C reaction-subdiffusion process, Phys. Rev. E 69 (3) (2004) 036126.
- Benson, D., Wheatcraft, Meerschaer, S. M. Application of a fractional advection-dispersion equation, Water Resour. Res. 36 (6) (20 0 0) 1403–1412.
- M. Hall, T. Barrick, From diffusion-weighted MRI to anomalous diffusion imaging, Magn. Reson. Med. 59 (3) (2008) 447–455.
- Henry, B. Langlands, T., Wearne, S. Fractional cable models for spiny neuronal dendrites, Phys. Rev. Lett. 100 (12) (2008) 128103.
- Raberto, M. Scalas, E. Mainardi, F.Waiting-times and returns in high-frequency financial data: an empirical study, Physica A 314 (1) (2002) 749–755
- Kilbas A. A., Srivastava H. M. and Trujillo J. J. «Theory and Applications of Fractional Differential Equations,» North-Holland Mathematics Studies, Vol. 204, 2006.
- Miller K. S. and. Ross B. «An Introduction to the Fractional Calculus and Fractional Differential Equations,» John Wiley, New York, 1993.
- Podlubny I. «Fractional Differential Equations,» Aca- demic Press, San Diego, New York, London, 1999.
- Самко С. Г., Килбас А. А., Маричев О. И. Интегралы и производные дробного порядка, и некоторые их приложения. — Минск: Наука и техника, 1987. — 688 с.
- Нахушев А. М. Дробное исчисление и его применение. М.: Физматлит, 2003. 272 с.
- Учайкин В. В. Метод дробных производных. Ульяновск: Артишок, 2008. 512 с.
- Псху А. В. Уравнения в частных производных дробного порядка. М.: Наука. 2005. 199 с.
- Аблабеков Б. С. Обратные задачи для псевдопараболических уравнений.- Бишкек: Илим, 2001. –183 с.
- Аблабеков, Б.С., Аблабекова, А.Б., Расулова, А. Р. Обратная задача определения временного источника в уравнении диффузии с дробными по времени производными, Вестник Ошского государственного университета. Математика. Физика. Техника. 2023. № 2 (3). С. 6–14.
- Аблабеков, Б.С., Жуман кызы, А . О разрешимости первой начально-краевой задачи для одномерного псевдопараболического уравнения с дробными производными, Вестник Ошского государственного университета. 2022. № 1. С. 29–37.
- Аблабеков, Б.С., Жуман кызы, А . О разрешимости второй начально-краевой задачи для одномерного псевдопараболического уравнения с дробными производными, Молодой ученый. 2022. № 18 (413). С. 1–5.
- Аблабеков Б. С., Аблабекова А. Б., Мамышева З. Э. О классической разрешимости одной начально-краевой задачи для модифицированного уравнения Аллера с дробной по времени производными, Наука, новые технологии и инновации Кыргызстана. 2023. № 1. С. 3–9.

