Ключевые слова: NTRUEncrypt, криптография, постквантовая криптография, решетки, шифрование, задача кратчайшего вектора.

Введение

За последние месяцы мир квантовых технологий переживает настоящий прорыв, о чём свидетельствуют новости с последних конференций и форумов. Например, на Форуме «Квант‑2025» в Москве, собравшем свыше 400 ведущих экспертов, были представлены результаты по расширению магистральных квантовых сетей, совершенствованию компонентов квантовых процессоров и разработке новых методов интеграции квантовых коммуникаций с криптографическими протоколами. Эти достижения демонстрируют, что квантовые технологии не только быстро развиваются, но и открывают новые горизонты в области обработки, передачи и защиты информации.

В условиях, когда квантовые алгоритмы, такие как алгоритм Шора [7], уже доказали свою способность факторизовать большие числа за полиномиальное время, традиционные криптографические системы (например, RSA и криптография на эллиптических кривых) оказываются под угрозой. Именно поэтому переход к постквантовой криптографии становится критически важным. Среди наиболее перспективных решений — криптосистемы, основанные на решётках, где безопасность обеспечивается сложностью таких NP‑трудных задач, как например задача кратчайшего вектора, на которой основан NTRUE [6].

Криптосистема NTRUEncrypt, разработанная ещё в 1996 году, остаётся одним из первых и наиболее изученных примеров такого подхода. Её математическая база позволяет обеспечить стойкость даже в условиях использования квантовых вычислительных систем, поскольку решение задачи кратчайшего вектора остаётся вычислительно неосуществимым для квантовых алгоритмов [1].

Криптосистема полагается на предполагаемую сложность факторизации определённых полиномов в усечённом кольце полиномов в частное двух полиномов с очень малыми коэффициентами. Взлом системы тесно связан, хотя и не эквивалентен, с алгоритмической задачей редукции решёток в некоторых типах решёток. Для защиты от известных атак требуется тщательный выбор параметров [2].

Так как и шифрование, и расшифровка требуют только простого умножения полиномов, эти операции выполняются значительно быстрее по сравнению с другими асимметричными схемами шифрования, такими как RSA, ElGamal и ECC [1].

Криптосистема NTRUEncrypt была разработана в 1996 году математиками Джеффри Хоффштейном, Джилл Пайфер и Джозефом Сильверманом, а также Даниэлем Лиманом, которые основали компанию NTRU Cryptosystems, Inc.

С момента её создания криптосистема была улучшена для повышения производительности и безопасности, включая ускорение операций и добавление новых параметров для защиты от известных атак. До 2005 года упоминались проблемы с расшифровкой, но позже они были устранены.

Сейчас NTRUEncrypt включён в стандарт IEEE P1363.1 для криптографии на основе решёток и принят в качестве стандарта X9.98 для финансовых приложений. Благодаря высокой скорости и низкому потреблению памяти, система подходит для мобильных устройств и смарт-карт [3].

Дополнительный стимул для дальнейшего развития данной области придают образовательные инициативы. Так, в Университете «Сириус» запущены программы дополнительного образования по квантовой информатике и информационной безопасности, что свидетельствует о стратегической важности подготовки новых специалистов для работы в условиях наступления эпохи квантовых вычислений.

NTRUEncrypt

Прежде чем мы перейдем к разбору NTRUEnrypt, рассмотрим подробней проблему, лежащую в основе рассматриваемой системы.

Задача кратчайшего вектора (Shortest Vector Problem, SVP) SVP определяется следующим образом: дана решётка в , требуется найти кратчайший ненулевой вектор .

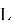
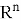
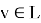
Формально:

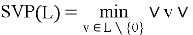
SVP известна как NP-трудная задача при использовании случайных редукций (например, редукций Грама–Шмидта), что делает её надёжным кандидатом для криптографических приложений. Эффективные алгоритмы для решения SVP могут иметь серьёзные последствия, потенциально делая многие криптографические схемы на основе решёток уязвимыми. [6]

Теперь разберем математическое устройство и операции, которые будут использоваться в дальнейшем.

Математический аппарат [4]

Операции NTRU основаны на объектах в усечённом кольце полиномов

со свёрточным умножением, где все полиномы в кольце имеют целые коэффициенты и степень не выше : Свойство в этом кольце приводит к тому, что умножение полинома на циклически сдвигает его коэффициенты. Отображение вида для фиксированного создаёт новый полином , в котором каждый коэффициент зависит от количества ненулевых коэффициентов в . Пусть даны два многочлена и с коэффициентами и соответственно, где . Тогда произведение данных многочленов с коэффициентами будет определяться следующим образом:

,

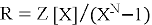
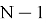
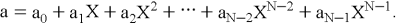
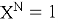
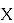
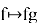
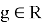
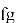
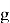
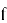
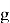
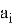
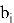
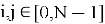
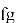
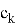
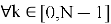
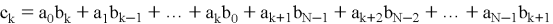
NTRU имеет следующие целочисленные параметры: , где — максимальная степень полинома, называется малым модулем, а — большим модулем. Предполагается, что является простым числом, всегда намного больше , а и взаимно просты. Открытые сообщения представлены в виде полиномов по модулю , а зашифрованные сообщения — в виде полиномов по модулю . Числа используются для определения «малости» полиномов соответственно [1].

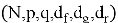
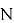
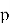
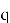
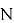
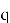
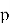
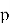
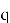
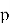
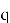
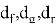
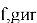
Отметим, что параметр служит для определения интервала, которому обязаны принадлежать все коэффициенты многочленов, используемых в криптосистеме.

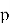
Пространство сообщений криптосистемы NTRU определяется как

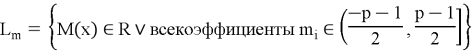
Вышеприведенные формулировки и обозначенные операции используется для построения алгоритмов криптографической системы защиты информации, которые глобально можно разбить на 3 этапа.

Этап 1 Генерация ключей [1]

Для передачи сообщения необходимы открытый и закрытый ключи. Открытый ключ доступен обеим сторонам, а закрытый ключ известен только принимающей стороне, которая использует его для генерации открытого ключа.

Для этого принимающая сторона выбирает два «маленьких» полинома и из кольца . Под «малостью» понимается, что коэффициенты полиномов значительно меньше , тогда как у произвольного полинома коэффициенты равномерно распределены по модулю . Малость полиномов определяется параметрами и . Полином имеет коэффициентов, равных 1, и коэффициентов, равных -1, остальные коэффициенты равны 0. Такой полином принадлежит множеству . Полином имеет коэффициентов, равных 1, и столько же коэффициентов, равных -1, остальные — 0. Такой полином принадлежит множеству .

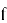
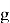
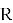
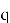
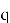
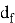
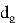
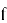
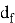
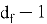
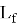
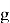
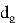
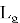
Выбор полиномов такого типа обусловлен тем, что может быть обратимым, а — нет (так как , а нулевой элемент не имеет обратного).

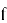
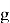
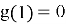
Выбранные полиномы и сохраняются в секрете. Затем вычисляются обратные полиномы и , такие что: Если не имеет обратного, выбирается другой полином.

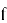
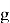
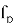
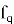
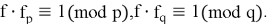
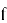
Секретный ключ состоит из пары . Открытый ключ вычисляется по формуле:

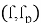
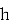
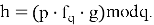
Этап 2 Шифрование [1]

Теперь, когда открытый ключ доступен отправителю, он может зашифровать сообщение для получателя. Для этого сообщение представляется в виде полинома с коэффициентами по модулю , которые выбираются из пространства сообщений . Таким образом, является «малым» полиномом по модулю .

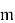
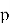
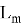
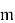
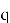
Затем отправитель выбирает «малый» полином , называемый «ослепляющим», который определяется параметром . Полином имеет коэффициентов, равных 1, и столько же коэффициентов, равных -1, остальные коэффициенты равны 0. Такой полином принадлежит множеству .

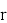
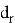
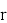
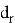
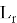
Используя полиномы , (открытый ключ) и , зашифрованное сообщение вычисляется по формуле: При этом любой, кто знает (или может вычислить) ослепляющий полином , сможет расшифровать сообщение .

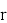
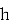
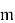
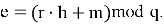
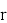
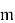
Этап 3 Расшифрование [1]

Теперь, получив зашифрованное сообщение , получатель может его расшифровать, используя свой секретный ключ. Для начала вычисляется промежуточный полином: Если подставить выражение для , то получается: . Окончательный вид:

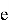
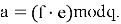
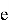
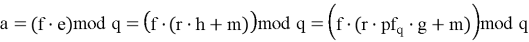
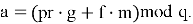
После вычисления по модулю , его коэффициенты приводятся к диапазону , после чего вычисляется полином , приведённый по модулю : поскольку Далее, используя вторую часть секретного ключа , получатель может расшифровать сообщение: Это выражение эквивалентно: Таким образом, результат является исходным сообщением .

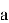
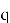
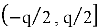
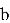
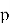
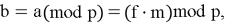
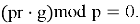
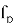
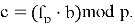
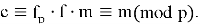
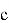
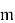
Не сложно заметить, что среди всех этапов работы NTRU‑Encrypt наиболее вычислительно затратным оказывается первый, так как поиск обратного по модулю полинома нетривиальная операция. [1] Эта операция значительно усложняет генерацию ключей и может стать серьёзным препятствием для аппаратных платформ с ограниченными ресурсами. Именно поэтому стандарт предусматривает несколько уровней стойкости — от умеренного до высочайшего — чтобы адаптироваться под разные требования: от лёгких встраиваемых устройств до высокопроизводительных серверов.

Рекомендованные параметры

Для достижения указанных уровней безопасности обратимся к рекомендованным параметрам стандарта отраженных в табл.1 [2].

Таблица 1

Рекомендованные параметры NTRUEncrypt

Подробней разберем значения, имеющиеся в таблице. Уровень стойкости — это значение показывающие количество базовых операций, которые потребуются самому эффективному методу атаки для дешифровки сообщения защищенного определённым методом NTRU. То есть уровень стойкости в 128 bit потребует от злоумышленника совершить элементарных операций, а если взять метод с стойкостью в 256 bit, то потребуется уже элементарных операций для взлома. Несложно заметить, что стоимость атаки экспоненциально растёт с увеличением этого “битового” показателя.

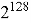
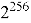
Теперь необходимо разобраться, что стоит за неизвестными аббревиатурами HPS и HRSS. Выше вводя метод генерации ключей один весьма важный момент был оставлен без объяснения, а именно определения параметров и . Метод HPS разработанный в 1996 г. и названный в честь авторов Hoffstein, Pipher и Silverman, это и есть тот способ, который был изложен выше. В этом варианте секретные полиномы и генерируются по фиксированному весу. Выбирается строго заданное число единиц и минус единиц, остальные коэффициенты равны нулю. Это упрощает анализ корректности схемы и позволяет подобрать минимально достаточное значение для обеспечения «идеальной корректности» дешифрования при заданном уровне стойкости [1]. Позже в 2017 г. был создан HRSS группой ученных Hülsing, Rijnveld, Schanck и Schwab. В этом методе каждый коэффициент , выбирается независимо равновероятно из (произвольный вес). Такой подход несколько увеличивает вариативность секретов и повышает устойчивость к некоторым видам атак за счёт уменьшения алгоритмической предсказуемости распределения [9].

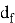
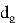
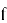
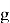
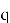
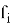
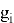
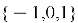
Но мир не стоит на месте: квантовые компьютеры уже не кажутся фантастикой, а атаки на классические схемы шифрования становятся всё более изощрёнными. Пока инженеры подбирают параметры для новых стандартов, криптоаналитики проводят бессонные ночи за редукцией решёток с чутьём на уязвимости.

На этом фоне важно не просто понимать, как работает NTRU, но и знать, какие существуют пути его криптоанализа. Даже самая стойкая криптосистема превращается в потенциальную мишень, если её параметры подобраны слабо или если новые методы анализа открывают ранее недоступные пути, поэтому устойчивость системы всегда следует рассматривать через призму актуальных и перспективных атак.

Атаки на алгоритм NTRU

Основные виды атак, можно условно разделить на три категории: атаки на основе редукции решёток, атака «встреча посередине» и гибридная атака. Теперь рассмотрим каждую из них поподробней.

Атаки на основе редукции решёток [10] [13]

Атаки этого типа эксплуатируют структуру решётки, формируемой публичным ключом . Решётка задаётся блочной матрицей:

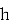
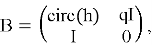
где — циркулянтная матрица, порождённая полиномом , — единичная матрица размерности , — большой модуль. Задача злоумышленника — найти в этой решётке вектор , соответствующий секретному ключу; длина этого вектора определяется числом ненулевых коэффициентов в полиномах и .

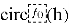
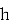
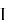
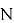
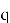
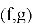
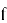
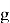
Стандартные алгоритмы редукции решёток (например, LLL или BKZ) применяются для уменьшения базиса и поиска коротких векторов. Оценка эффективности основана на гауссовской эвристике, дающей приближённую длину кратчайшего вектора

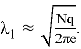
Сложность атак экспоненциально зависит от размерности и параметра безопасности , связанного с глубиной редукции.

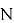
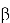
Например, чтобы гарантированно найти в решётке вектор длины порядка гауссовской эвристики , обычно берут . В результате получается , что по асимптотике часто упрощённо записывают как .

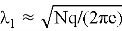
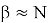
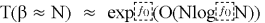
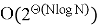
Если рассуждать в терминах «бит стойкости», который рассматривался выше, это означает, что для параметра при подборе модуля глубина редукции даёт эквивалент защиты примерно в бит, где константа (по лучшим эвристикам) лежит в районе 0.25–0.3. То есть сложность атаки оценивается как порядка операций. [13] Тогда при (уровень ~128 bit) BKZ-редукция займёт порядка операций, а При (уровень ~256 bit) время оценивается как операций.

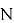
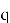
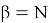
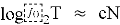
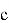
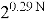
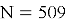
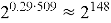
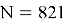
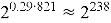
Атака «встреча посередине» (Meet-in-the-Middle) [5]

Идея метода заключается комбинаторном подходе. Полином , содержащий, например, ненулевых коэффициентов, разбивается на две части: и , каждая из которых содержит ненулевых элементов. Для каждого возможного вычисляется часть целевого вектора, и результаты сохраняются в хеш-таблице. Затем для каждого ищется совпадение — при успешном совпадении можно восстановить исходный ключ.

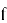
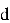
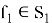
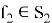
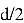
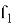
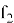
Сложность атаки составляет , что гораздо эффективнее полного перебора. Основной недостаток — высокая потребность в памяти, так как требуется хранить экспоненциальное количество векторов.

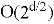
Гибридная атака [5]

Гибридный подход объединяет предварительную редукцию решётки с последующим применением meet-in-the-middle. Сначала решёточная база частично редуцируется до более низкой размерности , что позволяет уменьшить пространство поиска. Далее на оставшемся подпространстве выполняется атака «встреча посередине» с меньшими затратами по времени и памяти. Такой метод демонстрирует существенное ускорение по сравнению с чистой редукцией решёток при сохранении высокой вероятности успеха.

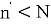
Гибридные методы считаются наиболее опасными при атаке на параметры с небольшим запасом прочности. Современные реализации BKZ с отбором и эвристиками, оптимизированными под структуры NTRU, значительно снижают фактический уровень стойкости при неудачном выборе параметров.

Сложность гибридной атаки выразить в виде единой «классической» формулы сложно, потому что итоговая сложность зависит от выбранного компромисса между глубиной редукции решётки (BKZ-блоком ) и объёмом памяти, отведённым на meet-in-the-middle. При этом обычно оптимизируют так, чтобы: где — время запуска BKZ с блоком , — «остаточный» вес (количество ) в полиноме, по которому делают MITM. Оптимально берут , и тогда обе части дают примерно одинаковый вклад.

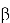
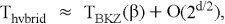
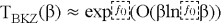
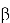
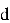
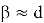
Теперь на примере из практики попробуем показать, в чем преимущество объединения первых двух способов. Впервые детальное бенчмаркирование гибридного подхода для NTRU-HPS (параметры , уровень безопасности ~128 bit) провели Ducas и Nguyen (2012) [1]. По их результатам, получилось следующее, что чистая BKZ-атака на этих параметрах требовала порядка операций, а гибридный метод (частичная BKZ-редукция до блока + MITM по ) снизил время до примерно операций при использовании памяти. Таким образом, гибридный подход сэкономил порядка 37 бит стойкости (с 148 down to 111) за счёт значительного потребления памяти и дополнительной сложности по организации MITM-поиска.

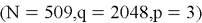
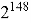
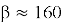
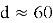
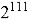
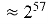
Анализ существующих атак показывает, что криптостойкость NTRUEncrypt напрямую зависит от параметров схемы. Например, рекомендованные значения из RFC 8391 [2] — для уровня безопасности 128 бит — основаны на устойчивости к современным методам редукции решёток и учёте комбинаторных атак. Для более высокой безопасности, например, 256 бит, параметры должны увеличиваться: , как указано в спецификациях NTRU-HPS и NTRU-HRSS [14].

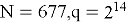
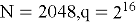
Также важно учитывать форму распределения полиномов : шаблоны HPS и HRSS сдвигают баланс между безопасностью и производительностью, повышая устойчивость к meet-in-the-middle и гибридным стратегиям [14].

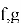
Таким образом, грамотный выбор параметров позволяет эффективно противостоять известным типам атак, поддерживая требуемый уровень стойкости без чрезмерных потерь в производительности. В следующем разделе мы сравним два ключевых семейства параметров NTRU — HPS и HRSS — и определим, какие из них наиболее подходят под конкретные сценарии применения — от IoT-устройств до защищённых серверных решений.

Также важно уточнить, что для приведения реализации NTRUEncrypt в соответствие с современными требованиями безопасности следует обеспечить константное время исполнения всех критических операций дешифрования (преобразования полиномов, вычитания и восстановления сообщения), что полностью устраняет утечки по таймингу, описанные в Technical Report #021 Silverman & Whyte (2005) [15]. Кроме того, базовый алгоритм остаётся уязвим к адаптивным атакам по выбранному шифртексту при отсутствии надёжной схемы заполнения, поэтому рекомендуется оборачивать NTRU в KEM/DEM-конструкцию с доказанной IND-CCA безопасностью: например, используя Fujisaki–Okamoto трансформацию или схему NAEP (Non-Adaptive Error Padding) [8], как это формализовано в стандарте RFC 9180 для HPS-варианта NTRU KEM.

Заключение

Заключая, можно сказать, что развитие квантовых технологий радикально трансформирует подходы к обеспечению информационной безопасности. Современные конференции и форумы, такие как «Квант‑2025», демонстрируют, что прогресс в области создания масштабируемых квантовых сетей и усовершенствованных квантовых процессоров уже сегодня становится катализатором перехода к новым криптографическим методам. Классические системы защиты, основанные на факторизации и дискретном логарифме, постепенно утрачивают свою надёжность в свете квантовых алгоритмов, что подчеркивает необходимость внедрения постквантовых решений.

Стоит отметить, что NTRUEncrypt, несмотря на свою новаторскую природу и стойкость перед квантовыми атаками, не получил широкого распространения. Причины заключаются в вычислительной сложности ключевой математической задачи, лежащей в основе алгоритма, а также в значительных ресурсах, необходимых для генерации ключей. Эти аспекты обусловили выбор альтернативных криптографических систем, которые демонстрируют лучшую производительность.

Тем не менее, NTRUEncrypt остаётся значимым вкладом в развитие постквантовой криптографии, задавая стандарты для исследований в области решёточных алгоритмов.

Литература:

1. Hoffstein, J. NTRU: A ring-based public key cryptosystem / J. Hoffstein, J. Pipher, J. H. Silverman. — Текст: непосредственный // Algorithmic Number Theory: Lecture Notes in Computer Science.. — 1998. — № 1423. — С. 267–288.
2. RFC 8391. NTRUEncrypt Parameter Sets and Encryption Algorithm. — Текст: электронный // Internet Engineering Task Force: [сайт]. — URL: https://tools.ietf.org/html/rfc8391 (дата обращения: 28.05.2025).
3. Security Innovation’s NTRUEncrypt Adopted as X9 Standard for Data Protection. — Текст: электронный // businesswire: [сайт]. — URL: https://web.archive.org/web/20220812083036/http://www.businesswire.com/news/home/20110411005309/en/Security-Innovation %E2 %80 %99s-NTRUEncrypt-Adopted-X9-Standard-Data (дата обращения: 28.05.2025).
4. NTRU. Algorithm Specifications and Supporting Documentation. — Текст: электронный // NTRU: [сайт]. — URL: https://ntru.org/f/ntru-20190330.pdf (дата обращения: 28.05.2025).
5. Smart, N. P. A Hybrid Lattice-Reduction and Meet-in-the-Middle Attack Against NTRU / N. P. Smart. — Текст: непосредственный // Advances in Cryptology — EUROCRYPT. — Berlin: Lecture Notes in Computer Science, 2007. — С. 135–154.
6. Micciancio, D. The Shortest Vector Problem is NP-Hard to Approximate within Some Constant / D. Micciancio. — Текст: непосредственный // Journal of the ACM. — 2001. — № 1423, часть 1. — С. 789–808
7. Shor, P. W. Algorithms for quantum computation: discrete logarithms and factoring / P. W. Shor. — Текст: непосредственный // Proceedings 35th Annual Symposium on Foundations of Computer Science. — Santa Fe: IEEE, 1994. — С. 124–134.
8. Hofheinz, D. A Modular Analysis of the Fujisaki-Okamoto Transformation / D. Hofheinz, K. Hövelmanns, E. Kiltz. — Текст: непосредственный // Theory of Cryptography. — Baltimore, MD, USA: Springer, Cham, 2017. — С. 341–371.
9. NTRU-HRSS-KEM Algorithm Specifications And Supporting Documentation. — Текст: электронный // Cryptojedi: [сайт]. — URL: https://cryptojedi.org/papers/ntrunistr1–20171130.pdf (дата обращения: 28.05.2025).
10. Ducas, L. Learning a parallelogram: cryptanalysis of NTRU / L. Ducas, P. Q. Nguyen. — Текст: непосредственный // Advances in Cryptology — EUROCRYPT. — Berlin: Lecture Notes in Computer Science, 2012. — С. 414–431.
11. Lenstra, A. K. Factoring polynomials with rational coefficients / A. K. Lenstra, H,W Lenstra, L. Lovász. — Текст: непосредственный // Mathematische Annalen. — Amsterdam:, 1982. — С. 515–534.
12. Schnorr, C. P. Lattice basis reduction: Improved practical algorithms and solving subset sum problems / C. P. Schnorr, M. Euchner. — Текст: непосредственный // Mathematical Programming. — 1994. — № 66. — С. 181–199.
13. Gama, N. Predicting lattice reduction / N. Gama, P. Q. Nguyen. — Текст: непосредственный // Advances in Cryptology — EUROCRYPT. — Berlin: Lecture Notes in Computer Science., 2008. — С. 31–51.
14. Paradise, F. Polynomial equation in algebraic attack on NTRU-HPS and NTRU-HRSS / F. Paradise, K. A. Sugeng. — Текст: непосредственный // ITM Web of Conferences. — Bali, Indonesia: EDP Sciences, 2024. — С. 341–371.
15. Silverman, J. H. Report # 021, Version 1 Timing Attacks on NTRUEncrypt via Variation in the Number of Hash Calls / J. H. Silverman, W. Whyte. — Текст: непосредственный // NTRU Cryptosystems Technical Report. —: NTRU Cryptosystems, Inc., 2006. — С. 341–371.