Моделирование асинхронного двигателя с переменными IR – Ψm на выходе интегрирующих звеньев в системе абсолютных единиц в Simulink
Емельянов Александр Александрович, доцент;
Бесклеткин Виктор Викторович, ассистент;
Пестеров Дмитрий Ильич, студент;
Вотяков Александр Сергеевич, студент;
Коровин Вадим Олегович, студент;
Соснин Александр Сергеевич, студент
Российский государственный профессионально-педагогический университет (г. Екатеринбург)
Быстрых Денис Анатольевич, начальник конструкторско-технологического бюро
АО «Уральский турбинный завод» (г. Екатеринбург)
Данная работа является продолжением статьи [1]. Проекции векторов ![]() и
и ![]() выведены на основе интегрирующих звеньев с моделированием в Simulink.
выведены на основе интегрирующих звеньев с моделированием в Simulink.
В работе [1] было получено уравнение (13) для расчета IRx в Script-Simulink:
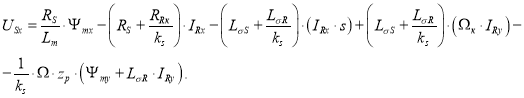
Перенесем 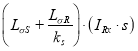 в левую часть:
в левую часть:

Обозначим:
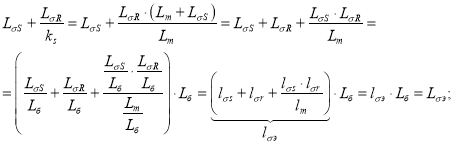
![]()
Выразим ток IRx по оси (+1):
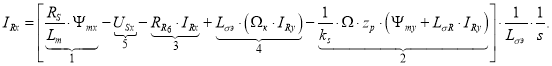
Структурная схема для определения тока IRx приведена на рис. 1.
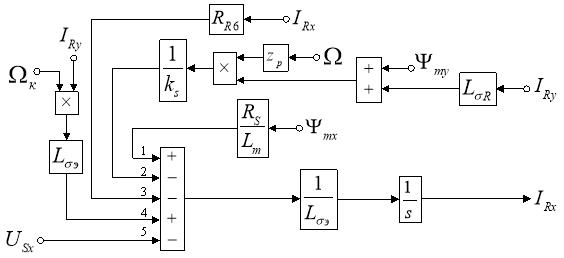
Рис. 1. Структурная схема для определения тока IRx в Script-Simulink
Преобразуем структурную схему на рис. 1 в оболочку, позволяющую производить расчет коэффициентов в отдельном блоке Subsystem. Для этого вместо операторов с коэффициентами, рассчитываемыми в Script, установим блоки перемножения, к которым подведены сигналы с результатами расчетов в Simulink, как показано на рис. 2.
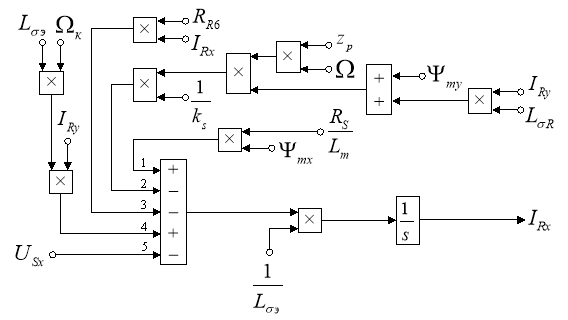
Рис. 2. Структурная схема для определения тока IRx в Simulink
Для определения потокосцепления Ψmx приведем уравнение (14) из работы [1]:
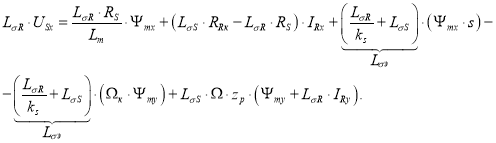
Перенесем 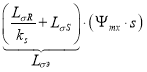 в левую часть:
в левую часть:
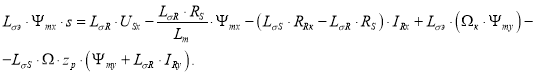
Обозначим:
![]()
![]()
Определим Ψmx по оси (+1):
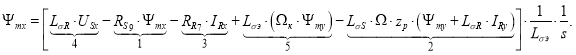
Структурная схема для определения потокосцепления Ψmx приведена на рис. 3.
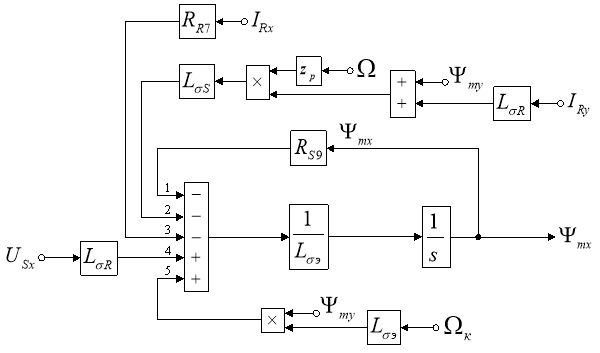
Рис. 3. Структурная схема для определения потокосцепления Ψmx в Script-Simulink
Расчет коэффициентов будем производить в отдельном блоке Subsystem, поэтому вносим в структурную схему на рис. 3 блоки перемножения (рис. 4).
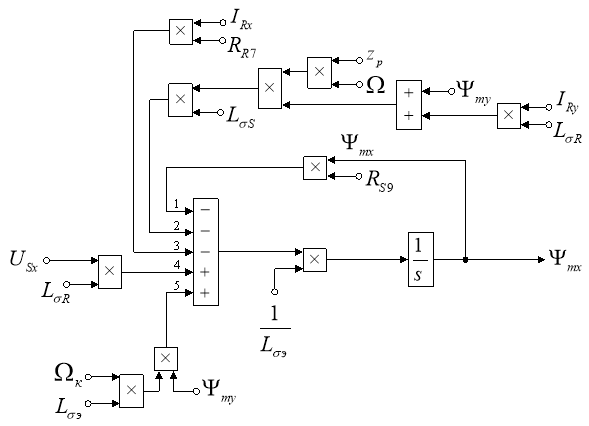
Рис. 4. Структурная схема для определения потокосцепления Ψmx в Simulink
Аналогично определим ток IRy и потокосцепление Ψmy по оси (+j).
Приведем уравнение (17) из работы [1]:
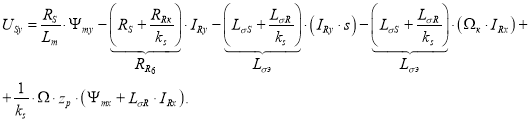
Перенесем 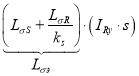 в левую часть:
в левую часть:
![]()
Определим ток IRy по оси (+j):
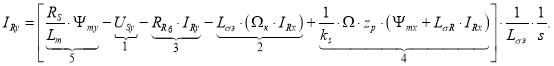
Структурная схема для определения тока IRy представлена на рис. 5.
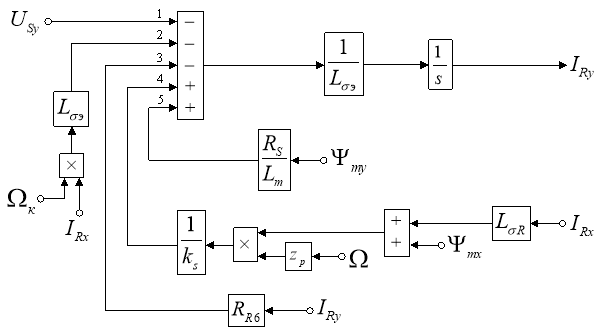
Рис. 5. Структурная схема для определения тока IRy в Script-Simulink
Схема для расчета IRy в Simulink представлена на рис. 6.
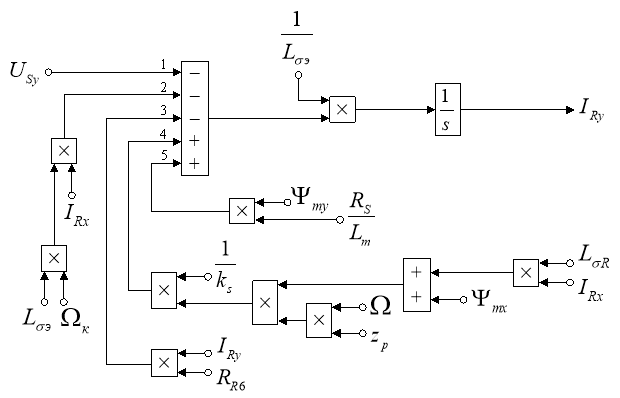
Рис. 6. Структурная схема для определения тока IRy в Simulink
Для определения потокосцепления Ψmy приведем уравнение (18) из работы [1]:
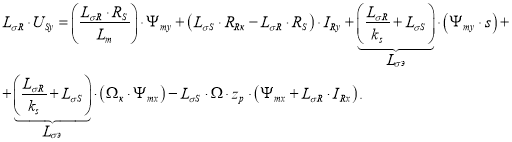
Перенесем 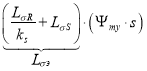 в левую часть:
в левую часть:
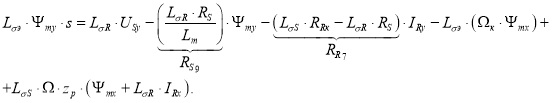
Выразим потокосцепление Ψmy по оси (+j):
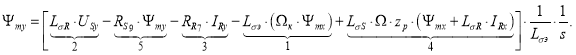
Структурная схема для определения Ψmy представлена на рис. 7.
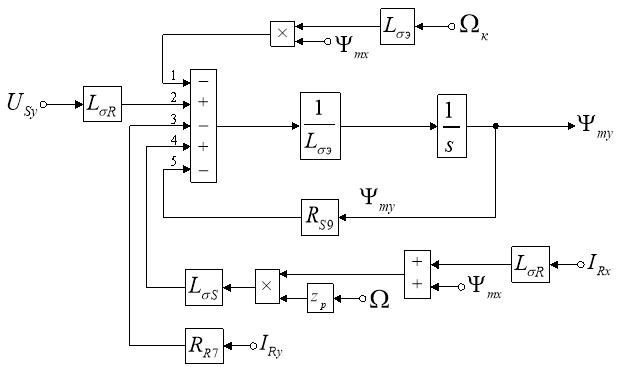
Рис. 7. Структурная схема для определения потокосцепления Ψmy в Script-Simulink
Схема для расчета Ψmy в Simulink дана на рис. 8.
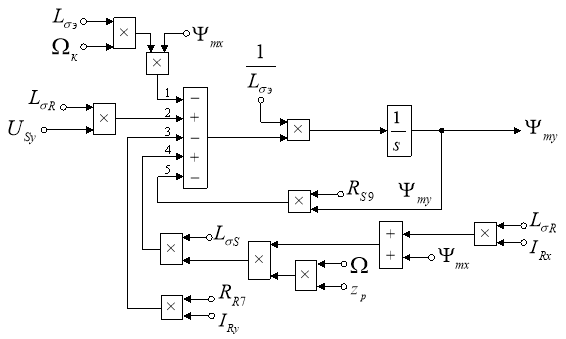
Рис. 8. Структурная схема для определения потокосцепления Ψmy в Simulink
На рис. 9 представлена структурная схема для реализации уравнения электромагнитного момента:
![]()

Рис. 9. Математическая модель определения электромагнитного момента M в Simulink
Из уравнения движения выразим механическую угловую скорость вращения вала двигателя (рис. 10):
![]()
![]()
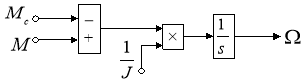
Рис. 10. Математическая модель уравнения движения в Simulink
Математическая модель асинхронного двигателя с короткозамкнутым ротором с переменными IR – Ψm на выходе интегрирующих звеньев в системе абсолютных единиц в Simulink дана на рис. 11, …, 15.
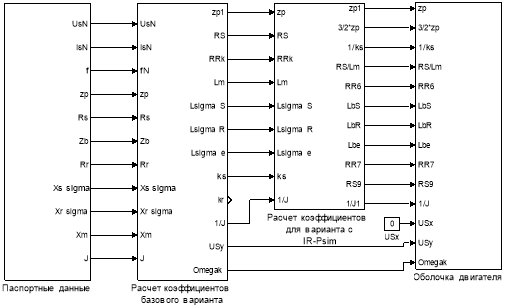
Рис. 11. Общая схема математической модели асинхронного двигателя с переменными IR – Ψm на выходе интегрирующих звеньев в системе абсолютных единиц в Simulink
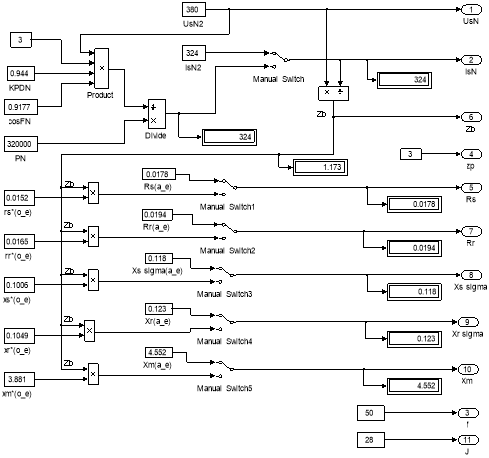
Рис. 12. Паспортные данные
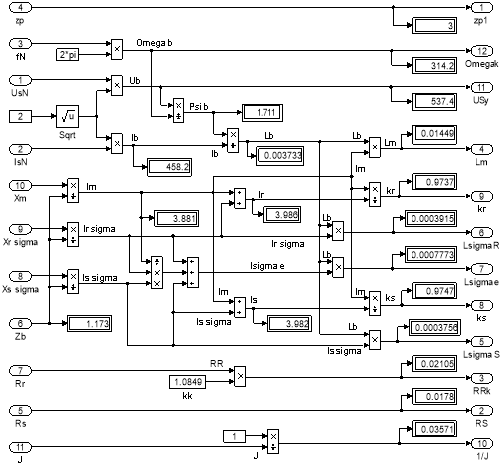
Рис. 13. Расчет коэффициентов базового варианта
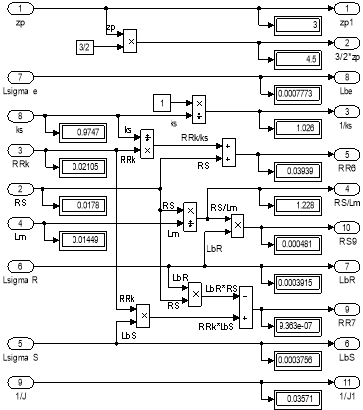
Рис. 14. Расчет коэффициентов для варианта с переменными IR– Ψm
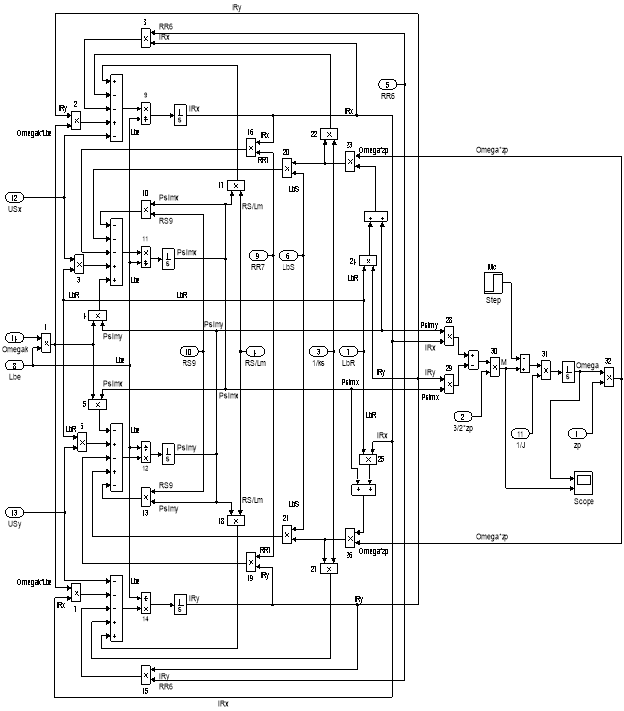
Рис. 15. Оболочка модели асинхронного двигателя с переменными IR – Ψm на выходе интегрирующих звеньев в системе абсолютных единиц в Simulink
Эту же схему можно представить в более компактной форме с использованием блоков Goto и From (рис. 16) и отдельных субблоков с расчетами токов и потокосцеплений, приведенных на рис. 17, …, 20.
Результаты моделирования асинхронного двигателя представлены на рис. 21.
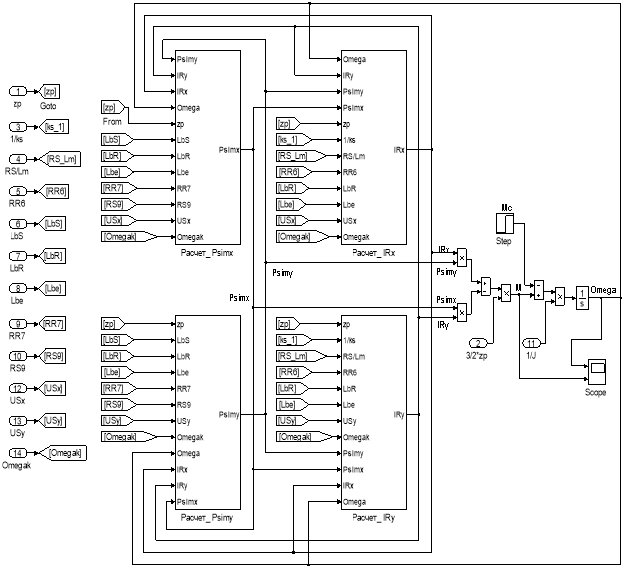
Рис. 16. Оболочка модели асинхронного двигателя с применением блоков Goto и From
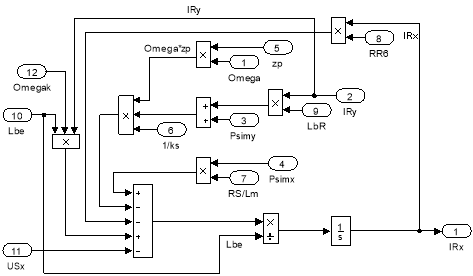
Рис. 17. Схема для расчета тока IRx
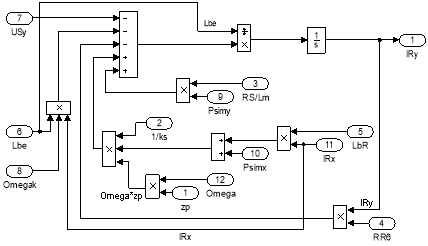
Рис. 18. Схема для расчета тока IRy
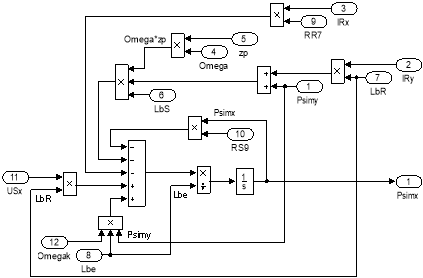
Рис. 19. Схема для расчета потокосцепления Ψmx
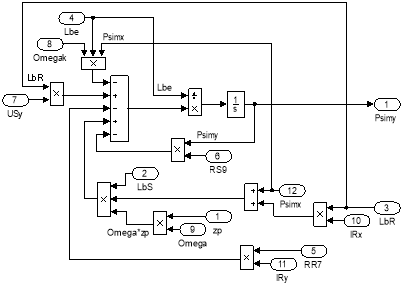
Рис. 20. Схема для расчета потокосцепления Ψmy
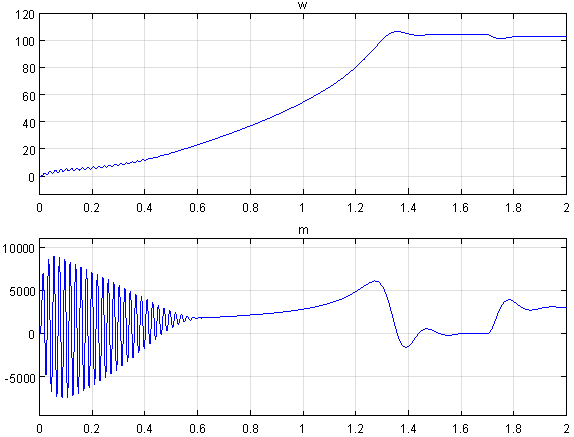
Рис. 21. Графики скорости и момента
Литература:
- Емельянов А.А., Бесклеткин В.В., Пестеров Д.И., Вотяков А.С., Захаров А.О., Соснин А.С., Быстрых Д.А. Моделирование асинхронного двигателя с переменными IR – Ψm на выходе апериодических звеньев в системе абсолютных единиц в Simulink-Script // Молодой ученый. - 2017. - №49.
- Шрейнер Р.Т. Математическое моделирование электроприводов переменного тока с полупроводниковыми преобразователями частоты. – Екатеринбург: УРО РАН, 2000. - 654 с.
- Шрейнер Р.Т. Электромеханические и тепловые режимы асинхронных двигателей в системах частотного управления: учеб. пособие / Р.Т. Шрейнер, А.В. Костылев, В.К. Кривовяз, С.И. Шилин. Под ред. проф. д.т.н. Р.Т. Шрейнера. - Екатеринбург: ГОУ ВПО «Рос. гос. проф.-пед. ун-т», 2008. - 361 с.

