Актуальность моей работы заключается в том, что в настоящее время, с развитием научно-технического прогресса, при многократно возросших объемах информации возникает проблема сжатия данных.
Для сжатия информации применяется кодирование. Так как при кодировании сокращается время передачи информации, а скорость передачи информации увеличивается. Применение кодирования позволяет решать целый спектр научно-технических проблем. Наиболее существенная из них это связь с дальним космосом.
А закодировать информацию можно с помощью теории графов.
На основе этой теории Дэвид Хаффман разработал свой алгоритм еще в 1952 году.
Закодировать можно любую информацию (текстовую, графическую), а в данной работе я рассмотрела кодирование только текстовой информации.
Поэтому цель работы: С помощью алгоритма Хаффмана закодировать сообщение для сжатия информации.
Отсюда следуют задачи, которые я поставила перед собой:
– рассмотреть основные понятия из теории графов,
– изучить алгоритм Хаффмана,
– построить кодовое дерево,
– закодировать информацию, вычислить коэффициент сжатия.
Я изучила теорию графов, основные понятия из теории графов: Граф — это средство для наглядного представления состава и структуры системы. Граф состоит из вершин, связанных дугами или ребрами. Я так же рассмотрела- граф, не содержащий циклов, или ациклический граф, и связный граф.
Одной из разновидностей графов является дерево.
Двоичное дерево — дерево, у которого из каждого узла выходит только две дуги.
Кодирование — это преобразование сообщений в сигнал, т. е.
Для кодирования текстовой информации я изучила алгоритм Хаффмана.
Рассмотрела процесс декодирования — процесс обратный кодированию.
Рассмотрим пример передачи информации на дальние расстояния с космической исследовательской станции. Ценность информации очень высока. Передающий абонент сильно ограничен по времени передачи данных с целью маскировки своего местоположения.
Для этого предлагаю внедрить в исследовательский космический аппарат алгоритм эффективного кодирования информации по методу Хаффмана. Тем самым получим уменьшенный объём информации
Как я это делала. Например, с космической станции надо передать сообщение: «Воды на Марсе не обнаружено». Применяю метод
1) Посчитаю количество символов в данном сообщении, их 28
2) Найду частоты появления (вероятности) символов и занесу их в таблицу
Таблица 1
|
М |
а |
т |
е |
м |
и |
к |
|
- |
ц |
р |
в |
с |
х |
н |
у |
. |
|
1_ 30 |
6_ 30 |
2_ 30 |
2_ 30 |
1_ 30 |
2_ 30 |
2_ 30 |
4_ 30 |
1_ 30 |
2_ 30 |
1_ 30 |
1_ 30 |
1_ 20 |
1_ 30 |
1_ 30 |
1_ 30 |
1_ 30 |
Составлю столбцы вероятностей символов, сверху вниз от большей вероятности к меньшей, если вероятности символов совпадают, то выше ставим ту, принадлежащий к которой символ первый стоит в предложении. Две последние вероятности складываем, и ставим в конец равных ей вероятностей, проделываем это — пока не получится 1.
Составляем кодовое дерево по построенной таблице.
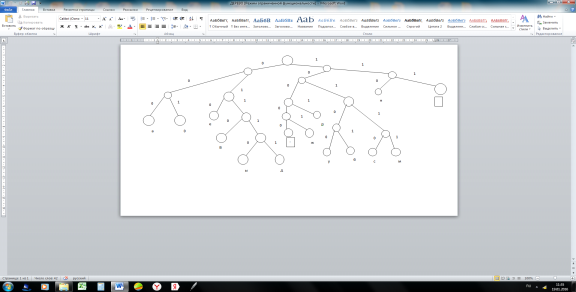
Рис. 1.
По кодовому дереву присваиваем каждому символу бинарный код.
Соединяю коды символов в единый передаваемый текст. Рассчитываю объем получившейся информации — получилось 104 бита.
Сосчитаю объем информации без кодирования, получил 224 бита. Затем нахожу коэффициент сжатия по формуле: получилось — 2 целых две тринадцатых
Вывод: алгоритм Хаффмана сжал информацию так, что скорость передачи данного текста увеличится, а время — уменьшится.
Можно произвести обратный процесс декодирования также по методу Хаффмана. Этот процесс важен принимающему информацию.
Даны частоты появления (вероятности) символов в таблице.
Составляем таблицу декодирования.
По таблице составляем кодовое дерево. С помощью высланной битовой последовательности проходим от корня к листу перемещаемся вправо если встретили 1 и влево если 0 проделываем это пока не расшифруем битовую последовательность.
Я также сравнила этот алгоритм с алгоритмом Шенона-Фано, но алгоритм Хаффмана оказался эффективнее и помехоустойчивым.
Составила сравнительную характеристику методов.
Заключение
– рассмотрены основные понятия из теории графов,
– изучен алгоритм Хаффмана,
– построено кодовое дерево,
– информация закодирована,
– найден коэффициент сжатия.
В моем проекте проделана процедура декодирования информации с заданными условиями.
С помощью графов решать задачи очень удобно, интересно, увлекательно. В настоящее время теория графов охватывает большой материал и активно развивается.
Литература:
- Березина Л. Ю. Графы и их применение. — М.: Просвещение, 1979. — 143 с. с ил.
- Камерон П., ван Линт Дж. Теория графов, теория кодирования и блок-схемы — М.:Наука, 1980, 140 стр.
- Фурсов В.А. Лекции по теории информации: Учебное пособие под редакцией Н.А. Кузнецова. — Самара: Издательство Самар. гос. аэрокосм. ун-та, 2006. — 148 с.: ил.

