Статья посвящена комплексному исследованию определению координат наземного подвижного объекта в сетях GSMи UMTS. Представлен метод для определения собственных координат на борту наземного подвижного объекта без использования запросов центра коммутации. Компьютерным моделированием с помощью пакета прикладных программ MatLAB оценены характеристики точности полученного алгоритма.
Ключевые слова и фразы: базовая станция, наземный подвижный объект, система GSMпозиционирования, спутниковая навигационная система.
Article is devoted complex research to definition of co-ordinates of land mobile object in networks GSM and UMTS. The method for definition of own co-ordinates onboard mobile object without use of inquiries of the centre of switching is presented. Computer modelling by means of a package of applied programs MatLAB estimates characteristics of accuracy of the received algorithm.
Введение.
Для определения координат и параметров движения подвижных наземных объектов в последнее время широко используются навигационные системы [1–4]. Состав навигационных систем определяется исходя из необходимости определения текущих координат местоположения подвижного объекта методом счисления и коррекции счисленных координат. Для коррекции координат в навигационных системах широкое применение нашли среднеорбитальные спутниковые радионавигационные системы ГЛОНАСС (глобальная спутниковая навигационная система) и NAVSTAR (Navstar — Navigational Satellite Time and Ranging — навигационный спутник измерения времени и координат) или по ее фактическому назначению GPS. Основными достоинствами данных радионавигационных систем являются: неограниченная дальность действия; высокая точность; однозначность навигационных определений; возможность измерения углов ориентации; высокая помехоустойчивость; неограниченность числа обслуживаемых объектов.
В результате приема и алгоритмической обработки сигналов данных систем приемная аппаратура подвижного наземного объекта, определяет координаты объекта, вектор скорости движения и текущее время. Однако, наряду с достоинствами спутниковых навигационных систем им присущи и недостатки. Это, прежде всего подверженность, как и всех радиотехнических измерителей, воздействию помех и трудности определения местоположение абонента в городе с плотной застройкой из-за многолучевости распространения радиосигнала.
Совершенствование систем навигации подвижных наземных объектов возможно за счет применения систем, принцип действия которых основан на применение новых технологий. В качестве таких систем целесообразно использование сотовой наземной радиотехнической инфраструктуры с наращиванием ее дополнительными базовыми и контрольно-корректирующими станциями [4].
В настоящее время сотовые операторы предлагают услуги по определению местоположения абонента [5]. Решение задачи местоопределения абонента в сетях сотовой связи началось с простейшего метода — Cell ID. Этот метод базируется на определении местоположения абонента с точностью до соты. Погрешность местонахождения таким способом достаточно низка и может доходить до 30 км. Существуют и другие методы позиционирования в сетях GSM и UMTS такие как Time of Arrival (TOA) и Observed Time Difference (OTD). Метод ТОА основан на измерении и сравнении интервалов времени прохождения сигнала от мобильного телефона до нескольких (не менее 3-х) базовых станций. Достигаемая при этом методе точность определения местоположения до 125 метров. Метод OTD базируется на измерении и сравнении интервалов времени прохождения сигналов от нескольких базовых станций до мобильного телефона. В данном методе можно достичь точность определения местоположения до 50 метров. Совмещение приемников сотовых телефонов с приемниками систем спутниковой навигации позволило разработать метод Assisted Global Positioning System (A-GPS) позволяющий определять текущее местоположение с точностью порядка 10 метров.
Существенным недостатком данных методов является необходимость запроса с целью использование самих базовых станций или центра коммутации для вычисления координат. При этом информация о местоположении выдается абоненту с задержкой, определяемой временим от получения запроса центром коммутации и вычисления координат местоположения до отправки сообщения о местонахождении абоненту.
Цель работы: разработка позиционным методом алгоритма определения на борту подвижного наземного объекта координат местоположения с использованием информацию о направлении приема сигналов от базовых станций GSM и исследование характеристик точности определения координат местоположения.
Постановка задачи. Пусть имеются две базовые станции GSM или UMTS с известными координатами 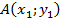 и
и 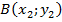 (рисунок 1). Считаем, что на борту подвижного наземного объекта с помощью узконаправленных антенн определяются углы азимута
(рисунок 1). Считаем, что на борту подвижного наземного объекта с помощью узконаправленных антенн определяются углы азимута 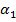 и
и 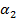 на первую и вторую базовую станцию соответственно. Необходимо, используя позиционный метод, определить координаты точки
на первую и вторую базовую станцию соответственно. Необходимо, используя позиционный метод, определить координаты точки 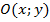 местоположения подвижного наземного объекта.
местоположения подвижного наземного объекта.
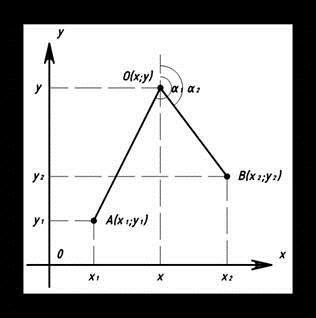
Рис. 1
Алгоритм определения местоположения объекта.
Координаты точки 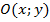 местоположения подвижного наземного объекта будем определять как точку пересечения двух прямых [6]. Для этого запишем уравнение прямой общего вида:
местоположения подвижного наземного объекта будем определять как точку пересечения двух прямых [6]. Для этого запишем уравнение прямой общего вида:
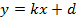 , (1)
, (1)
где 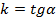 — тангенс угла наклона.
— тангенс угла наклона.
Зная координаты базовых станций, определим используя (1) величины 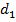 и
и 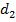 :
:
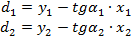 .
.
Запишем систему уравнений для нахождения координат точки 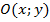 :
:
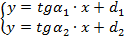 . (2)
. (2)
Подставим в систему (2) коэффициенты 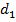 и
и 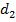 :
:
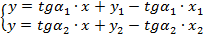 . (3)
. (3)
Решая систему (3), выразим координаты точки 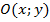 пересечения двух прямых:
пересечения двух прямых:
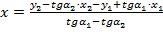 ; (4)
; (4)
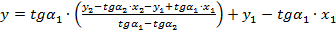 . (5)
. (5)
Полученные выражения (4) и (5) являются искомыми координатами подвижного наземного объекта. Для их вычисления необходимо знать координаты базовых станций A 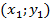 ; B
; B 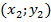 и углы азимута
и углы азимута 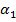 и
и 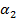 на эти станции.
на эти станции.
Исследование точностных характеристик алгоритма определения местоположения объекта.
Среднеквадратическое значение радиальной погрешности определения местоположения объекта будет определяется выражением:
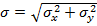 ,
,
где 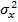 и
и 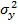 — дисперсии погрешностей определения координат местоположения объекта по осям ОX и ОY.
— дисперсии погрешностей определения координат местоположения объекта по осям ОX и ОY.
Погрешности вычисления координат объекта определяются равенствами:
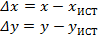 ,
,
где 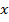 и
и 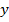 вычисленные координаты объекта;
вычисленные координаты объекта; 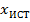 и
и 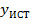 истинные значения координат объекта.
истинные значения координат объекта.
Как следует из (4) и (5) погрешности 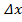 и
и 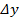 вызваны тем, что координаты базовых станций
вызваны тем, что координаты базовых станций 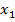 ,
, 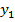 ,
, 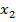 ,
, 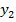 и углы азимута
и углы азимута 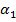 и
и 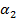 определяются с погрешностями. Полагаем, что погрешности являются взаимонезависимыми случайными величинами. Дисперсии погрешностей определения координат объекта по осям ОX и ОYсоответственно равны:
определяются с погрешностями. Полагаем, что погрешности являются взаимонезависимыми случайными величинами. Дисперсии погрешностей определения координат объекта по осям ОX и ОYсоответственно равны:
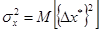 ,
,
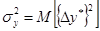 ,
,
где 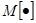 — означает операцию усреднения по множеству реализаций; индекс
— означает операцию усреднения по множеству реализаций; индекс 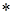 означает центрированное значение случайной величины.
означает центрированное значение случайной величины.
Для определения дисперсии 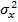 погрешности определения координаты местоположения объекта по оси ОX разложим в ряд Тейлора относительно истинных значений
погрешности определения координаты местоположения объекта по оси ОX разложим в ряд Тейлора относительно истинных значений 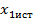 ,
, 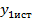 ,
, 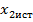 ,
, 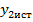 ,
, 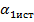 ,
, 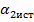 выражение (4). Ограничиваясь линейными членами разложения и полагая, что погрешности
выражение (4). Ограничиваясь линейными членами разложения и полагая, что погрешности 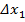 ,
, 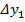 ,
, 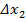 ,
, 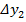 ,
, 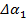 ,
, 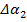 являются взаимонезависимыми случайными величинами, переходя к соответствующим дисперсиям погрешностей, получим:
являются взаимонезависимыми случайными величинами, переходя к соответствующим дисперсиям погрешностей, получим:
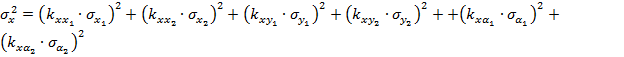 (6)
(6)
где 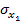 ,
, 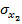 ,
, 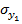 и
и 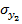 – среднеквадратические значения погрешностей определения координат базовых станций;
– среднеквадратические значения погрешностей определения координат базовых станций; 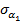 и
и 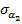 — среднеквадратические значения погрешностей определения азимутальных углов; коэффициенты
— среднеквадратические значения погрешностей определения азимутальных углов; коэффициенты 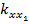 ,
, 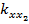 ,
, 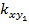 ,
, 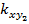 ,
, 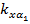 и
и 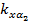 определяются частными производными относительно истинных значений координат базовых станций и азимутальных углов:
определяются частными производными относительно истинных значений координат базовых станций и азимутальных углов:
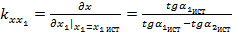 ;
;
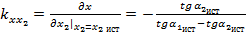 ;
;
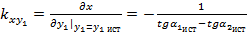 ;
;
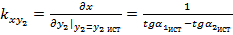 ;
;
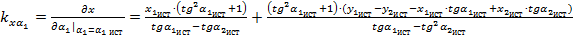 ;
;
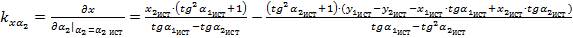 .
.
Для определения дисперсии 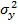 погрешности определения координаты местоположения объекта по оси ОY воспользуемся выражением (5). Проделав аналогичные операции, как и для определения дисперсии
погрешности определения координаты местоположения объекта по оси ОY воспользуемся выражением (5). Проделав аналогичные операции, как и для определения дисперсии 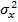 , получим:
, получим:
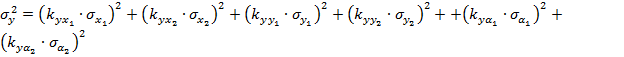 (7)
(7)
где коэффициенты 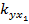 ,
, 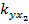 ,
, 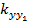 ,
, 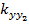 ,
, 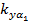 и
и 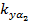 имеют вид:
имеют вид:
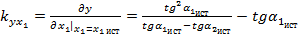 ;
;
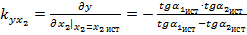 ;
;
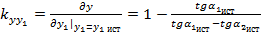 ;
;
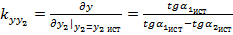 ;
;
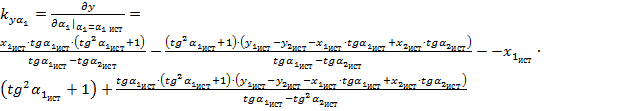 ;
;
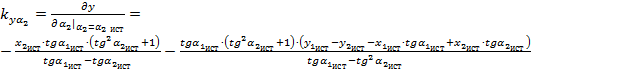 .
.
Вычисление среднеквадратических значений погрешностей определения координат местоположения объекта, согласно (6), (7), для определения среднеквадратического значения радиальной погрешности проводилось компьютерным моделированием с помощью пакета прикладных программ MatLAB. При вычислениях предполагалось что:
- среднеквадратические значения погрешностей определения координат базовых станций могут иметь значения 3, 5 и 10 ;
;
- значение разности углов азимута 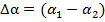 может находиться в пределах (
может находиться в пределах (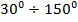 );
);
- ширина ДН приемных антенн может иметь значения: 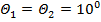 ;
; 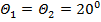 ;
; 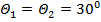 . Для выбранных значений ширины ДН антенн среднеквадратические значения погрешностей определения азимутных углов соответственно равны
. Для выбранных значений ширины ДН антенн среднеквадратические значения погрешностей определения азимутных углов соответственно равны 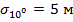 ,
, 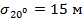 и
и 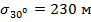 [7].
[7].
Результаты моделирования представлены на рисунках 2–4.
На рис. 2 представлены зависимости среднеквадратического значения радиальной погрешности определения местоположения объекта от разности углов азимута 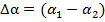 для трех среднеквадратических значений погрешностей определения координат базовых станций:
для трех среднеквадратических значений погрешностей определения координат базовых станций: 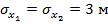 ,
, 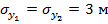 — кривая 1;
— кривая 1; 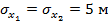 ,
, 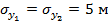 — кривая 2;
— кривая 2; 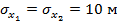 ,
, 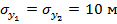
 – кривая 3. Расчеты выполнены для случая, когда ширина диаграммы направленности антенны равна
– кривая 3. Расчеты выполнены для случая, когда ширина диаграммы направленности антенны равна 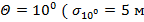 ).
).
На рис. 3 и рис. 4 представлены те же самые зависимости для ширины диаграммы направленности антенны 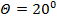 (
(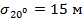 ) и ширины диаграммы направленности антенны
) и ширины диаграммы направленности антенны 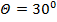 (
(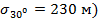 , соответственно.
, соответственно.
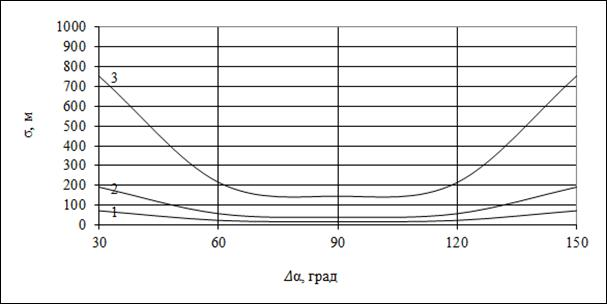
Рис. 2
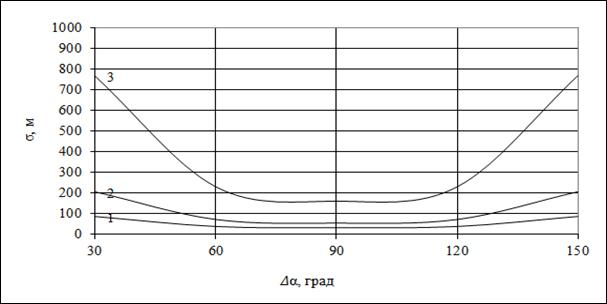
Рис. 3
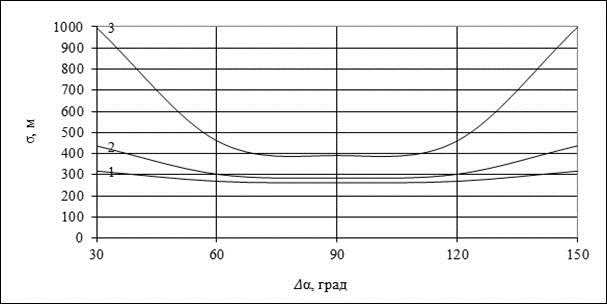
Рис. 4
Как видно из зависимостей, приведенных на рис.1 — рис. 3, максимальная точность определения координат местоположения подвижного наземного объекта достигается при разности углов азимута 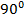 , что полностью совпадает с теорией. При этом следует отметить, что имеется достаточно большой диапазон отклонения от разности углов азимута
, что полностью совпадает с теорией. При этом следует отметить, что имеется достаточно большой диапазон отклонения от разности углов азимута 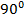 , в котором точность определения координат местоположения подвижного наземного объекта сохраняется почти постоянной. Кроме того точность позиционирования возрастает с ростом точности установки базовых станций на местности и уменьшением ширины диаграммы направленности антенн. При точности установки базовых станций на местности 3 м и применении узконаправленных антенн с шириной ДН
, в котором точность определения координат местоположения подвижного наземного объекта сохраняется почти постоянной. Кроме того точность позиционирования возрастает с ростом точности установки базовых станций на местности и уменьшением ширины диаграммы направленности антенн. При точности установки базовых станций на местности 3 м и применении узконаправленных антенн с шириной ДН 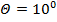 среднеквадратическое значение радиальной погрешности определения местоположения объекта имеет минимальную величину порядка 20 м, а при ширине ДН
среднеквадратическое значение радиальной погрешности определения местоположения объекта имеет минимальную величину порядка 20 м, а при ширине ДН 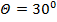 радиальная погрешность составляет 150 м. Данные значения сопоставимы с методами определения координат местоположения в сетях GSM (TOA, E-OTD), что позволяет применить данный метод на практике.
радиальная погрешность составляет 150 м. Данные значения сопоставимы с методами определения координат местоположения в сетях GSM (TOA, E-OTD), что позволяет применить данный метод на практике.
Так как в данном случае нет необходимости делать запросы на базовые станции, в отличие от приведенных выше методов, то можно вычислять свое местоположение с достаточно малым интервалом времени, что дает возможность использовать данную технологию для подвижных наземных объектов.
Литература:
1. Иванов, А. В. Комплексные оптимальные алгоритмы обработки информации в навигационных системах подвижных наземных объектов / А. В. Иванов // Радиотехника. — 2010, № 5.
2. Иванов, А. В. Комплексные оптимальные алгоритмы обработки информации в навигационных системах подвижных наземных объектов с контролем целостности навигационного обеспечения / А. В. Иванов // Радиотехника. — 2010, № 12.
3. Иванов, А. В. Навигационные системы подвижных наземных объектов. Алгоритмы обработки информации в угловом канале / А. В. Иванов // Радиотехника. — 2013, № 4.
4. Иванов, А. В. Совместная обработка информации спутниковых радионавигационных систем и наземных сетевых систем в навигационных системах подвижных наземных объектов [Текст]/А. В. Иванов, А. В. Гостев, А. А. Семенов, Л. В. Соколовская//Радиотехника. — 2012. — № 4. — С.4–10.
5. Ю. А. Громаков, А. В. Северин, В. А. Швецов Технологии определения местоположения в GSM и UMTS: Учеб. пособие. — М.: Эко-Трендз, 2005. — 144 с.
6. М. А. Дубинин Нахождение точки пересечения двух линий по углам и двум известным точкам (биангуляция) [Электронный ресурс]: — Режим доступа: http://gis-lab.info/qa/biangulation.html.
7. Белавин О. В. Основы радионавигации: Учебное пособие для вузов. — М.: Сов. радио, 1977. — 320 с.

