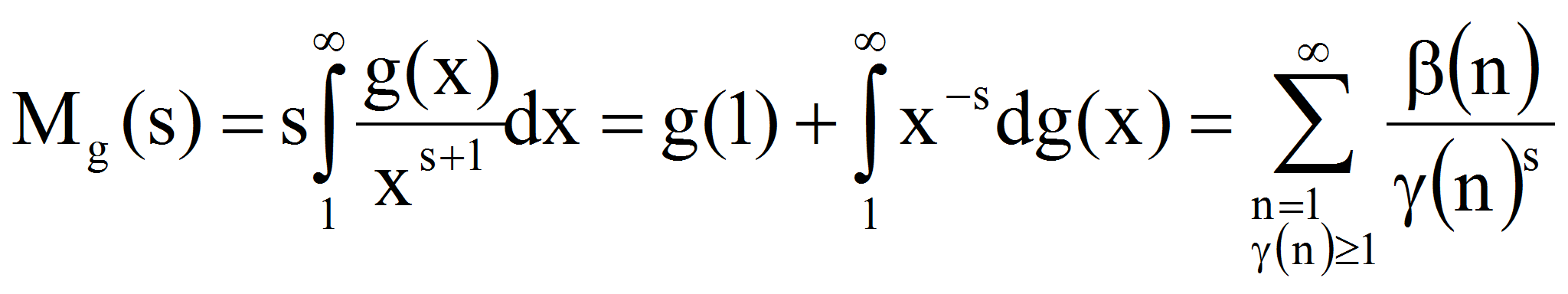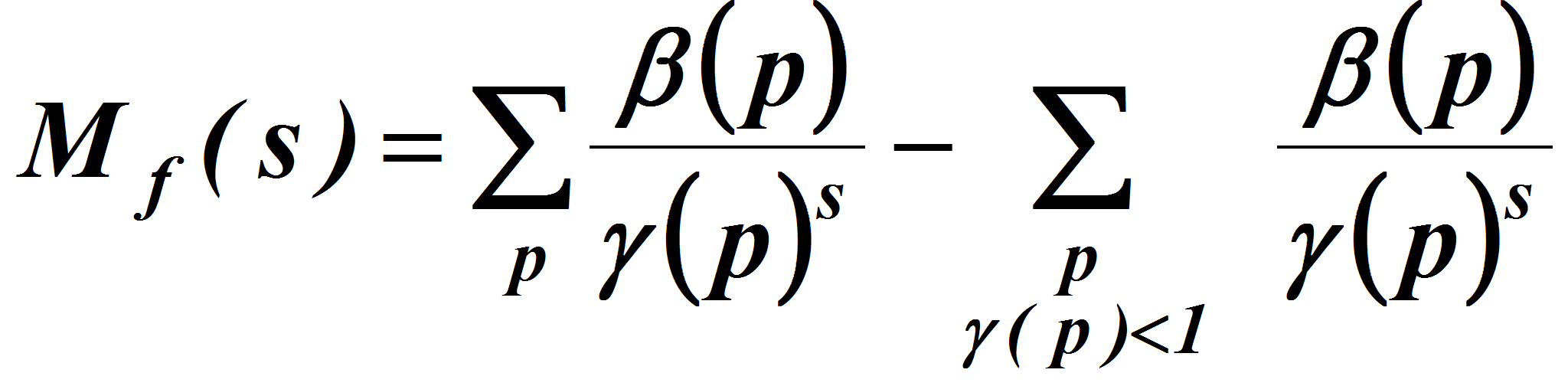Работа посвящена задачам, где изучается асимптотическое поведение суммы значений мультипликативных функций. Устанавливается связь между такими суммами по простым числам и натуральным числам. Результаты, полученные в работе, основаны на исследовании аналитических свойств указанных сумм и имеют приложения в теории свободных нормированных полугрупп.
Work is devoted problems where it is studied асимптотическое behavior of the sum of values of multiplicative functions. Connection between such sums on simple numbers and natural numbers is established. The results received in work, are based on research of analytical properties of the specified sums and have appendices in the theory free normative semi groups.
Пусть
![]() и
и
![]() − неотрицательные мультипликативные функции. Определим функции
− неотрицательные мультипликативные функции. Определим функции
![]() и
и
![]() следующим образом:
следующим образом:
(![]() −простые числа,
−простые числа,
![]() −
натуральные числа). Введем обозначения;
−
натуральные числа). Введем обозначения;
![]()
![]()
Учитывая определения функции
![]() и
и
![]() ,
имеем
,
имеем
Предположим, что ряд
![]() сходится в полуплоскости
сходится в полуплоскости
![]() .
.
Начиная с этого момента, мы предполагаем также, что
![]() для всех натуральных
для всех натуральных
![]() .
Так как все члены ряда
.
Так как все члены ряда
неотрицательные числа, то отсюда следует, что ряд
для
![]()
(а следовательно и ряд для
![]() )
при
)
при
![]() сходится абсолютно. Доказывается следующие теоремы:
сходится абсолютно. Доказывается следующие теоремы:
Теорема 1. Пусть
![]() и
и
![]() −
неотрицательные мультипликативные функции, причем
−
неотрицательные мультипликативные функции, причем
![]() для всех
для всех
![]() .
.
Тогда если ряды
Рассмотрим несколько следствий теоремы 1.
Следствие 1. Пусть
![]() &#;
неотрицательная мультипликативная функция
&#;
неотрицательная мультипликативная функция
![]() ,
,
![]() ,
,
![]() .
.
то
В частности, этим условиям удовлетворяет функция
![]() .
Поэтому отсюда следует закон простых чисел.
.
Поэтому отсюда следует закон простых чисел.
Следствие 2. Пусть
![]() &#;</FONT>
мультипликативная функция,
<A HREF="images/41792d49.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/41792d49.gif" NAME="Объект49" ALIGN=ABSMIDDLE WIDTH=57 HEIGHT=20></A>
для всех неотрицательных
<A HREF="images/mf0fa213.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/mf0fa213.gif" NAME="Объект50" ALIGN=ABSMIDDLE WIDTH=18 HEIGHT=18></A>.<P>
<A HREF="images/m229802b9.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m229802b9.gif" NAME="Объект51" ALIGN=ABSMIDDLE WIDTH=181 HEIGHT=47></A>,
<A HREF="images/6f67ba9f.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/6f67ba9f.gif" NAME="Объект52" ALIGN=ABSMIDDLE WIDTH=39 HEIGHT=18></A>,
<A HREF="images/m358502df.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m358502df.gif" NAME="Объект53" ALIGN=ABSMIDDLE WIDTH=39 HEIGHT=18></A>.<P>
Тогда если ряды
<P>
<A HREF="images/m24a70a01.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m24a70a01.gif" NAME="Объект54" ALIGN=ABSMIDDLE WIDTH=109 HEIGHT=45></A>
и
<A HREF="images/38552012.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/38552012.gif" NAME="Объект55" ALIGN=ABSMIDDLE WIDTH=81 HEIGHT=41></A>
<P>сходятся и
<P>
<A HREF="images/m5a3de862.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m5a3de862.gif" NAME="Объект56" ALIGN=ABSMIDDLE WIDTH=94 HEIGHT=45></A>
для всех простых
<A HREF="images/m66aee3d2.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m66aee3d2.gif" NAME="Объект57" ALIGN=ABSMIDDLE WIDTH=20 HEIGHT=18></A>,
<P>то<P>
<A HREF="images/731bd49c.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/731bd49c.gif" NAME="Объект58" ALIGN=ABSMIDDLE WIDTH=98 HEIGHT=41></A>.<P>
<I><B>Теорема 2.</B></I> Пусть
<A HREF="images/28709dc2.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/28709dc2.gif" NAME="Объект59" ALIGN=ABSMIDDLE WIDTH=39 HEIGHT=20></A>
и
<A HREF="images/5232127.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/5232127.gif" NAME="Объект60" ALIGN=ABSMIDDLE WIDTH=39 HEIGHT=18></A>−
неотрицательные, вполне мультипликативные функции,
<A HREF="images/1007a8cb.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/1007a8cb.gif" NAME="Объект61" ALIGN=ABSMIDDLE WIDTH=147 HEIGHT=18></A>
при всех простых
<A HREF="images/m66aee3d2.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m66aee3d2.gif" NAME="Объект62" ALIGN=ABSMIDDLE WIDTH=20 HEIGHT=18></A>.<P>
<A HREF="images/28020ad6.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/28020ad6.gif" NAME="Объект63" ALIGN=ABSMIDDLE WIDTH=201 HEIGHT=47></A>,
<A HREF="images/6f67ba9f.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/6f67ba9f.gif" NAME="Объект64" ALIGN=ABSMIDDLE WIDTH=39 HEIGHT=18></A>,
<A HREF="images/m358502df.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m358502df.gif" NAME="Объект65" ALIGN=ABSMIDDLE WIDTH=39 HEIGHT=18></A>,
(1)<P>
Тогда если ряд<P>
<A HREF="images/m65f79e67.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m65f79e67.gif" NAME="Объект66" ALIGN=ABSMIDDLE WIDTH=124 HEIGHT=44></A>
<P>сходится, то<P>
<A HREF="images/m5764b518.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m5764b518.gif" NAME="Объект67" ALIGN=ABSMIDDLE WIDTH=120 HEIGHT=42></A>.<P>
<I><B>Теорема 3.</B></I> Пусть
<A HREF="images/28709dc2.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/28709dc2.gif" NAME="Объект68" ALIGN=ABSMIDDLE WIDTH=39 HEIGHT=20></A>
и
<A HREF="images/5232127.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/5232127.gif" NAME="Объект69" ALIGN=ABSMIDDLE WIDTH=39 HEIGHT=18></A>−
неотрицательные мультипликативные функции,
<A HREF="images/1007a8cb.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/1007a8cb.gif" NAME="Объект70" ALIGN=ABSMIDDLE WIDTH=147 HEIGHT=18></A>
для всех простых
<A HREF="images/m66aee3d2.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m66aee3d2.gif" NAME="Объект71" ALIGN=ABSMIDDLE WIDTH=20 HEIGHT=18></A>
и выполнено условие (1).<P>
Тогда
<P>
<A HREF="images/m5764b518.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m5764b518.gif" NAME="Объект72" ALIGN=ABSMIDDLE WIDTH=120 HEIGHT=42></A>.<DL>
<DT>
Литература:</DL>
<OL>
<LI><P>
Файнлейб А.С. Некоторые асимптотические формулы для сумм
мультипликативных функций и их приложения.<FONT FACE="Symbol">&#;</FONT>
Литовский матем. сборник, 7, №13, 1967, 535-545.<LI><P>
Ингам А.Е. Распределение простых чисел.<FONT FACE="Symbol">&#;</FONT>
ОНТИ, 1936.<LI><P>
Титчмарш Е.К. Теория дзета-функции Римана.<FONT FACE="Symbol">&#;</FONT>
ИЛ, 1953.</OL>
&#;</FONT>
мультипликативная функция,
<A HREF="images/41792d49.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/41792d49.gif" NAME="Объект49" ALIGN=ABSMIDDLE WIDTH=57 HEIGHT=20></A>
для всех неотрицательных
<A HREF="images/mf0fa213.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/mf0fa213.gif" NAME="Объект50" ALIGN=ABSMIDDLE WIDTH=18 HEIGHT=18></A>.<P>
<A HREF="images/m229802b9.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m229802b9.gif" NAME="Объект51" ALIGN=ABSMIDDLE WIDTH=181 HEIGHT=47></A>,
<A HREF="images/6f67ba9f.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/6f67ba9f.gif" NAME="Объект52" ALIGN=ABSMIDDLE WIDTH=39 HEIGHT=18></A>,
<A HREF="images/m358502df.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m358502df.gif" NAME="Объект53" ALIGN=ABSMIDDLE WIDTH=39 HEIGHT=18></A>.<P>
Тогда если ряды
<P>
<A HREF="images/m24a70a01.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m24a70a01.gif" NAME="Объект54" ALIGN=ABSMIDDLE WIDTH=109 HEIGHT=45></A>
и
<A HREF="images/38552012.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/38552012.gif" NAME="Объект55" ALIGN=ABSMIDDLE WIDTH=81 HEIGHT=41></A>
<P>сходятся и
<P>
<A HREF="images/m5a3de862.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m5a3de862.gif" NAME="Объект56" ALIGN=ABSMIDDLE WIDTH=94 HEIGHT=45></A>
для всех простых
<A HREF="images/m66aee3d2.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m66aee3d2.gif" NAME="Объект57" ALIGN=ABSMIDDLE WIDTH=20 HEIGHT=18></A>,
<P>то<P>
<A HREF="images/731bd49c.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/731bd49c.gif" NAME="Объект58" ALIGN=ABSMIDDLE WIDTH=98 HEIGHT=41></A>.<P>
<I><B>Теорема 2.</B></I> Пусть
<A HREF="images/28709dc2.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/28709dc2.gif" NAME="Объект59" ALIGN=ABSMIDDLE WIDTH=39 HEIGHT=20></A>
и
<A HREF="images/5232127.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/5232127.gif" NAME="Объект60" ALIGN=ABSMIDDLE WIDTH=39 HEIGHT=18></A>−
неотрицательные, вполне мультипликативные функции,
<A HREF="images/1007a8cb.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/1007a8cb.gif" NAME="Объект61" ALIGN=ABSMIDDLE WIDTH=147 HEIGHT=18></A>
при всех простых
<A HREF="images/m66aee3d2.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m66aee3d2.gif" NAME="Объект62" ALIGN=ABSMIDDLE WIDTH=20 HEIGHT=18></A>.<P>
<A HREF="images/28020ad6.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/28020ad6.gif" NAME="Объект63" ALIGN=ABSMIDDLE WIDTH=201 HEIGHT=47></A>,
<A HREF="images/6f67ba9f.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/6f67ba9f.gif" NAME="Объект64" ALIGN=ABSMIDDLE WIDTH=39 HEIGHT=18></A>,
<A HREF="images/m358502df.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m358502df.gif" NAME="Объект65" ALIGN=ABSMIDDLE WIDTH=39 HEIGHT=18></A>,
(1)<P>
Тогда если ряд<P>
<A HREF="images/m65f79e67.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m65f79e67.gif" NAME="Объект66" ALIGN=ABSMIDDLE WIDTH=124 HEIGHT=44></A>
<P>сходится, то<P>
<A HREF="images/m5764b518.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m5764b518.gif" NAME="Объект67" ALIGN=ABSMIDDLE WIDTH=120 HEIGHT=42></A>.<P>
<I><B>Теорема 3.</B></I> Пусть
<A HREF="images/28709dc2.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/28709dc2.gif" NAME="Объект68" ALIGN=ABSMIDDLE WIDTH=39 HEIGHT=20></A>
и
<A HREF="images/5232127.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/5232127.gif" NAME="Объект69" ALIGN=ABSMIDDLE WIDTH=39 HEIGHT=18></A>−
неотрицательные мультипликативные функции,
<A HREF="images/1007a8cb.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/1007a8cb.gif" NAME="Объект70" ALIGN=ABSMIDDLE WIDTH=147 HEIGHT=18></A>
для всех простых
<A HREF="images/m66aee3d2.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m66aee3d2.gif" NAME="Объект71" ALIGN=ABSMIDDLE WIDTH=20 HEIGHT=18></A>
и выполнено условие (1).<P>
Тогда
<P>
<A HREF="images/m5764b518.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m5764b518.gif" NAME="Объект72" ALIGN=ABSMIDDLE WIDTH=120 HEIGHT=42></A>.<DL>
<DT>
Литература:</DL>
<OL>
<LI><P>
Файнлейб А.С. Некоторые асимптотические формулы для сумм
мультипликативных функций и их приложения.<FONT FACE="Symbol">&#;</FONT>
Литовский матем. сборник, 7, №13, 1967, 535-545.<LI><P>
Ингам А.Е. Распределение простых чисел.<FONT FACE="Symbol">&#;</FONT>
ОНТИ, 1936.<LI><P>
Титчмарш Е.К. Теория дзета-функции Римана.<FONT FACE="Symbol">&#;</FONT>
ИЛ, 1953.</OL>