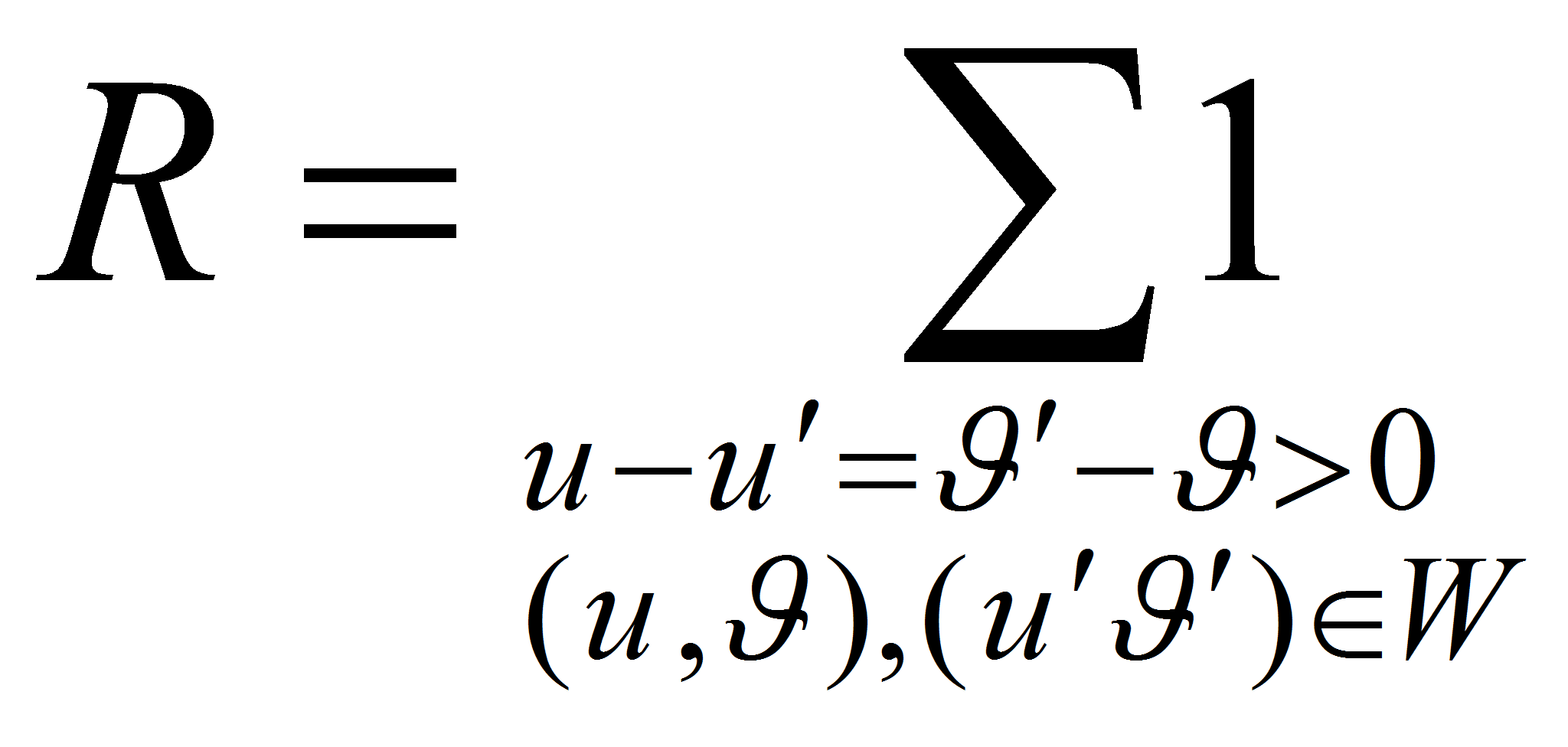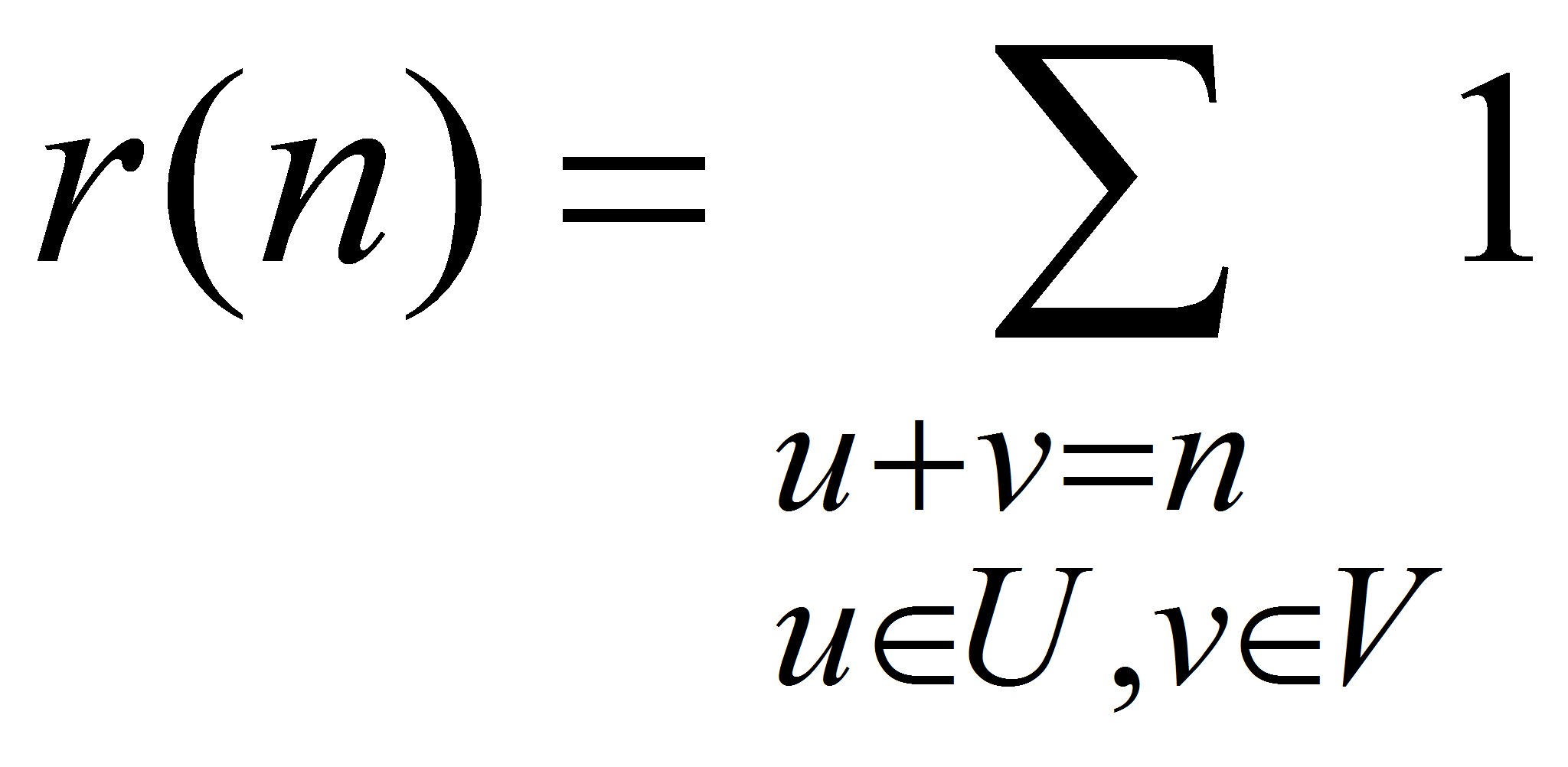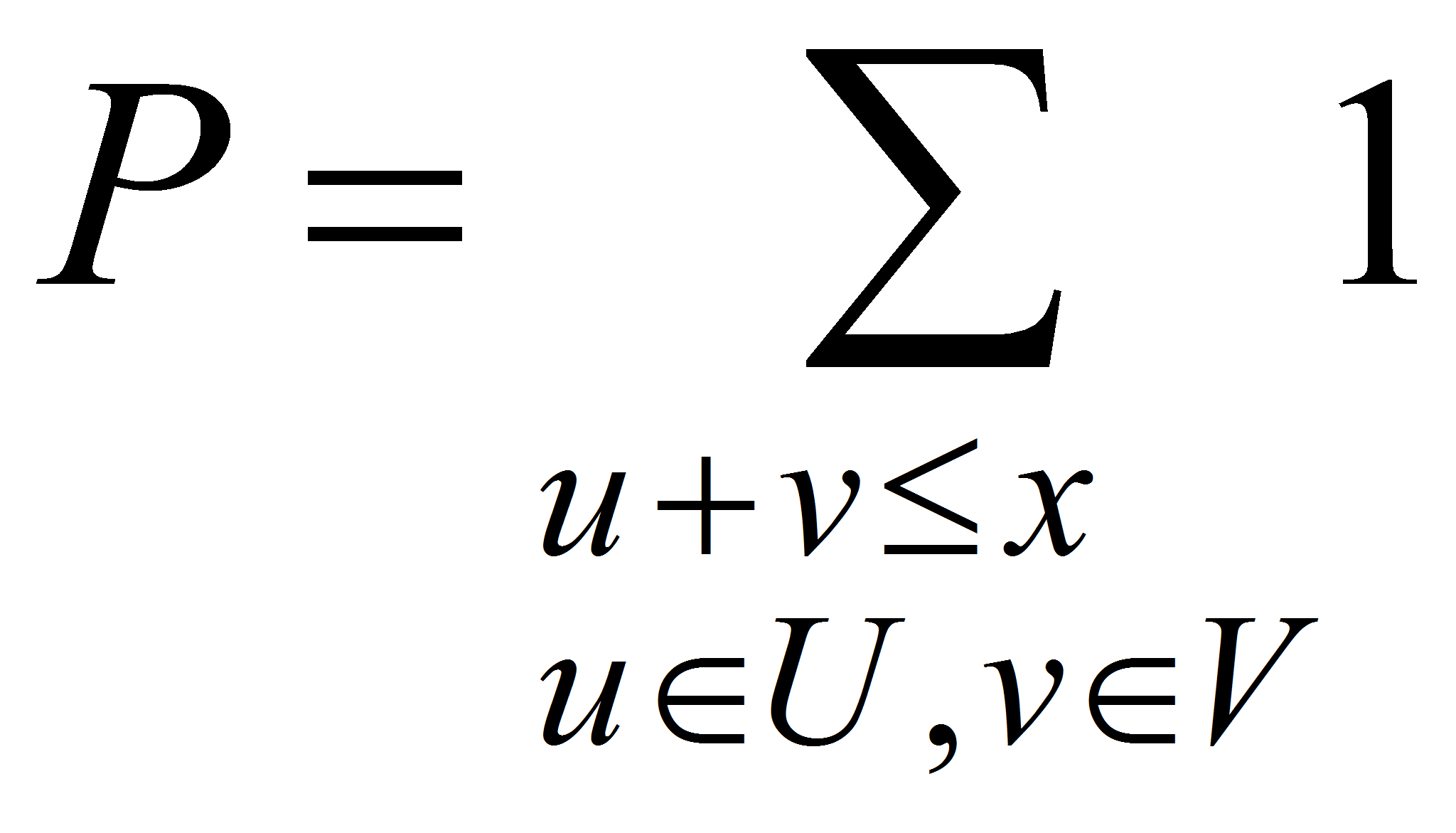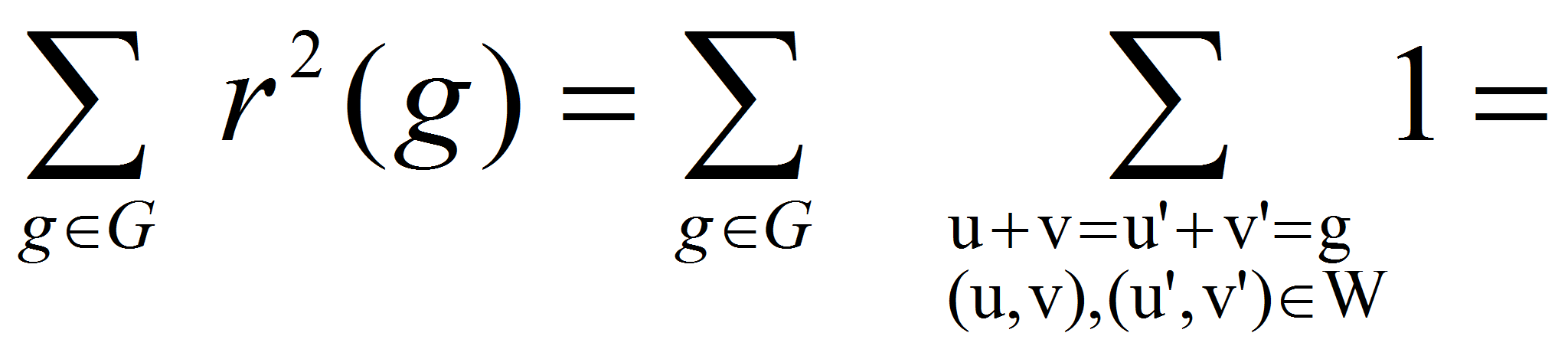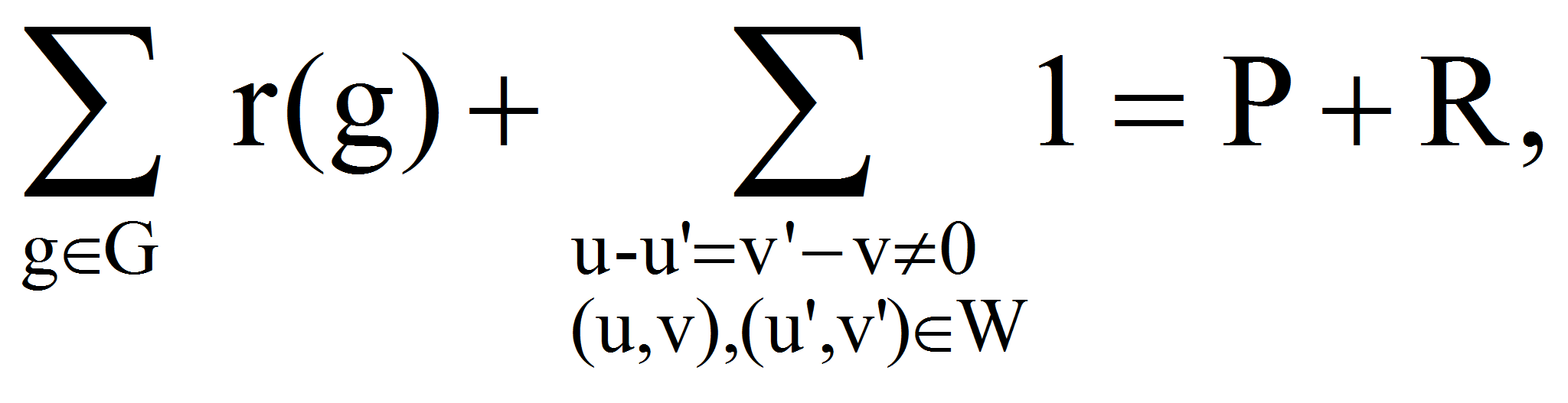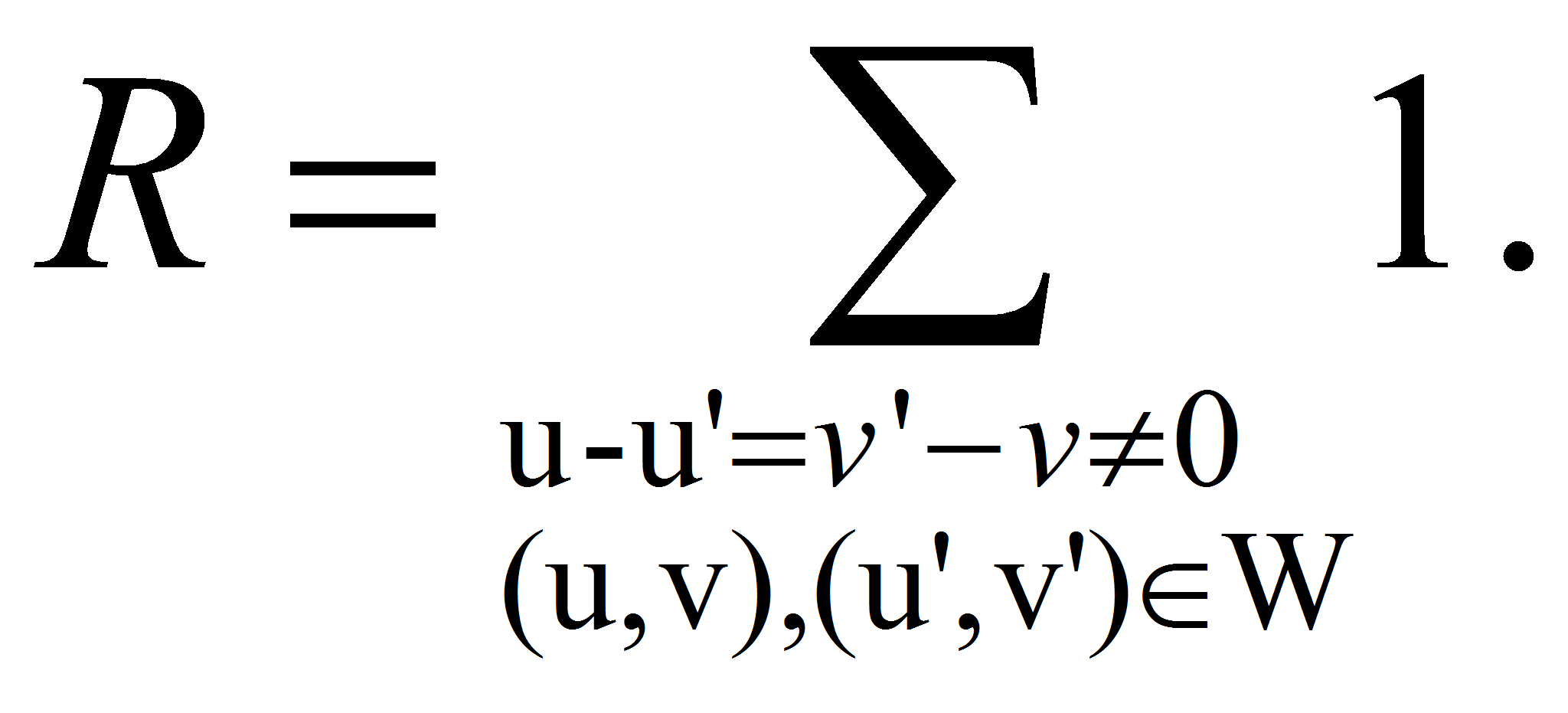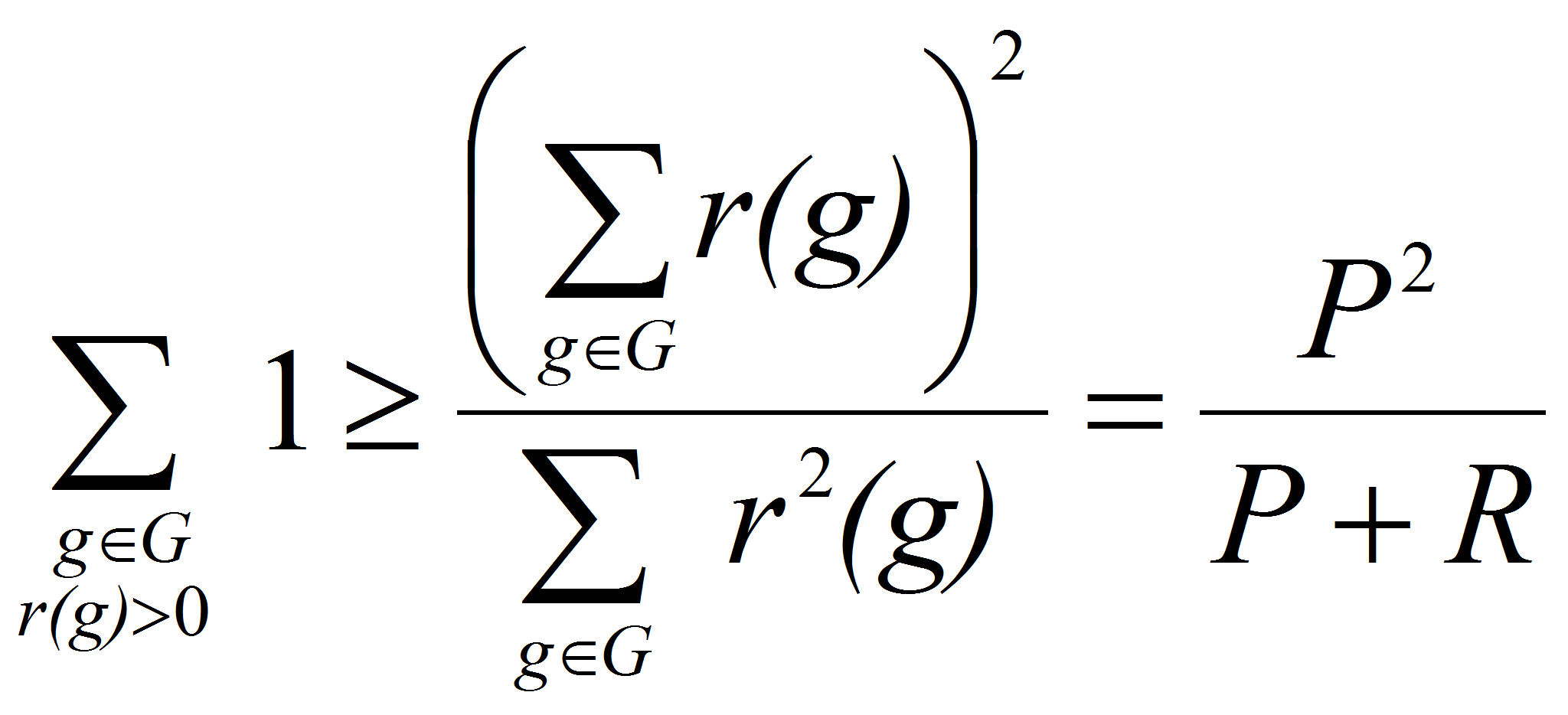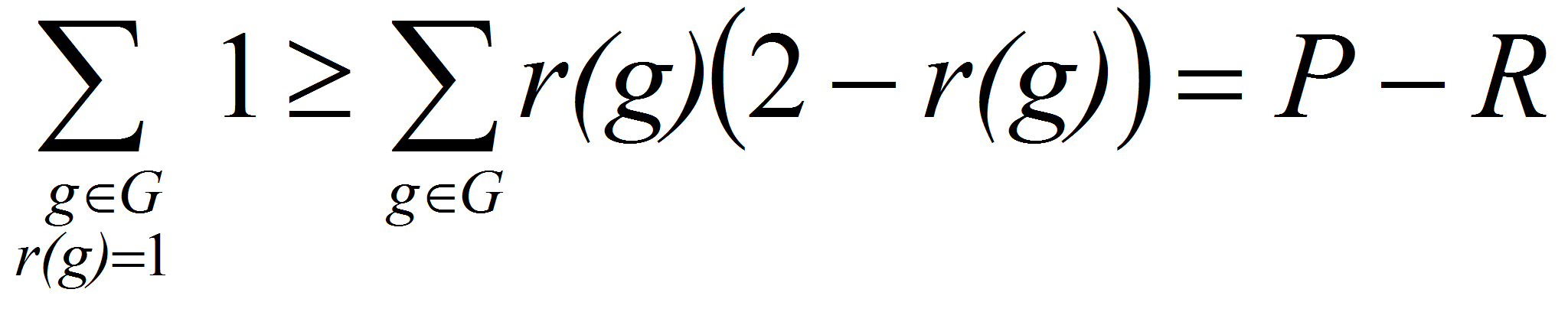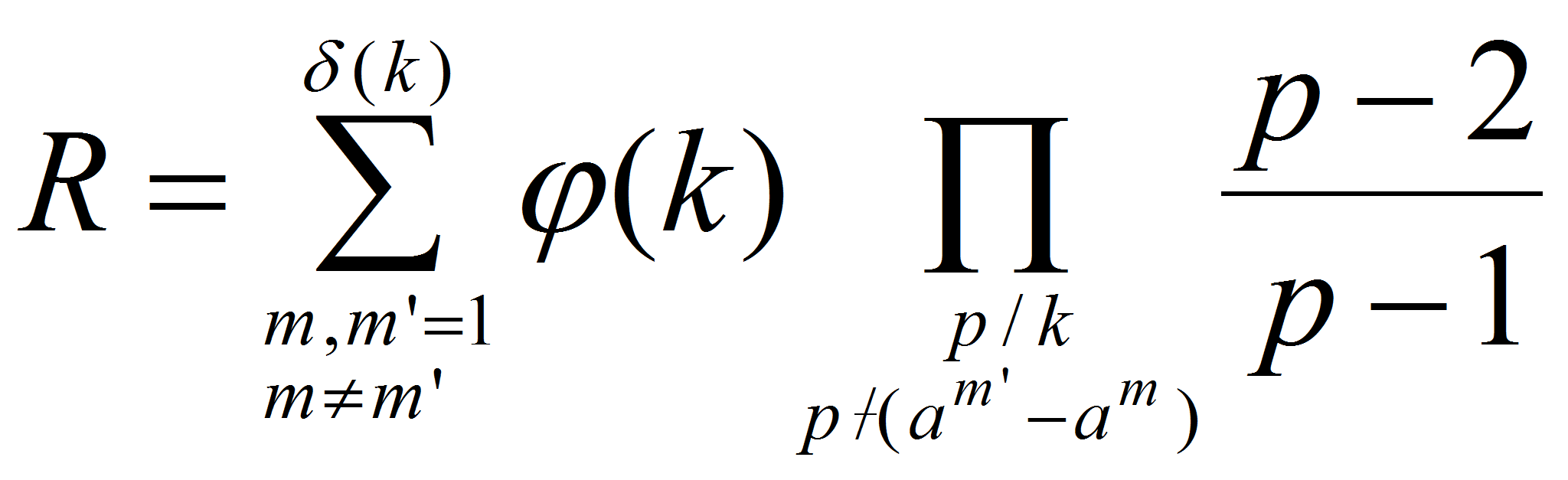Аналоги неравенств Романова-Шнирельмана и Романова Ердоша для аддитивной группы

В работе рассматривается задача об оценке снизу плотности представимых чисел в бинарной аддитивной задаче о сложении последовательностей натуральных чисел U u V в случае, когда U u V подмножества аддитивной абелевой группы . Показано, что наряду с тождеством Романова для группы справедливы также аналоги неравенств Романова-Шнирельмана и Романова-Эрдеша.

The work considers the issue of lower-bound estimate of density of represented numbers in a binary additive task on addition of sequences of natural number U and V in case where U and V are a subset of additive Abelian group G. It has been shown that along with Romanoff identical equation for group G analogues of Romanoff-Shnirelmann and Romanoff-Erdos inequalities are also correct.

В 1934-году Н.П.Романов [1] заметил, что оценки снизу плотности представимых чисел в бинарной аддитивной задаче о сложении последовательностей U u V можно свести к верхней оценки выражения

Основой для такого сведения является тождество

(тождество Романова) , (1)

где ,

При таких обозначениях величин R и P из (1) с помощью неравенства Коши-Буняковского получаем неравенства , (неравенства Романова- Шнирельмана)и (неравенства Романова-Ердоша)

(здесь N-число целых чисел промежутка[1,х], представимых в виде u+v, -число целых чисел промежутка[1,х], однозначно представимых в виде u+v,Отметим прежде всего, что тождество Романова можно обобщить на любую аддитивную группу.Пусть - аддитивная абелева группа, и - какие-либо подмножества группы , - некоторое конечное множество пар где Для каждого обозначим через - число представлений элемента в виде суммы где

Тогда

где - число пар множества ,

Заметим для дальнейшего, что наряду с тождеством Романова для аддитивной группы справедливы также аналоги неравенств Романова-Шнирельмана и Романова-Эрдеша. Действительно, в силу неравенств Коши

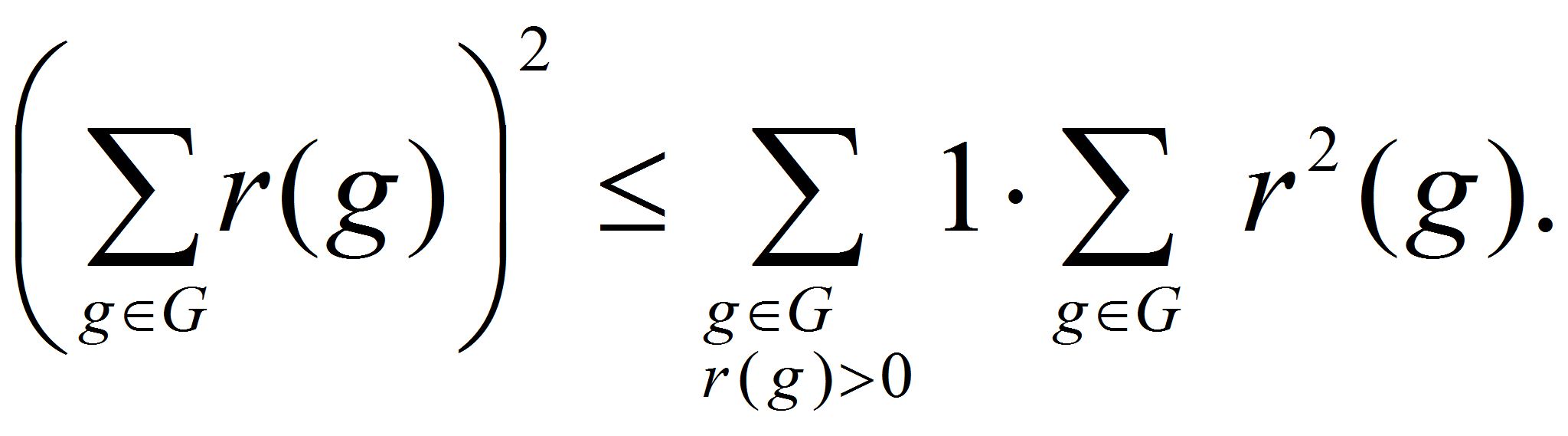
Отсюда и из тождества Романова следует

(аналог неравенства Романова-Шнирельмана). Далее,

(аналог неравенства Романова-Эрдеша). В интересующем нас случае для величины и получаем следующие оценки:

и

Литература:

1. Romanow N.P. Über limge satze der additiven Zahlentheorie, Math. Ann., 109 (1934) , 669&#;678.

2. Шнирельман Л.Г. Об аддитивных свойствах чисел.&#; Изв. Донского политехнического института,1 ч, 1930, 3&#;28.

3. Erdöş P. On additive properties of aquares of primes, Konikl Nederland Aad. Amst., 41.1 (1938), 37&#;41.