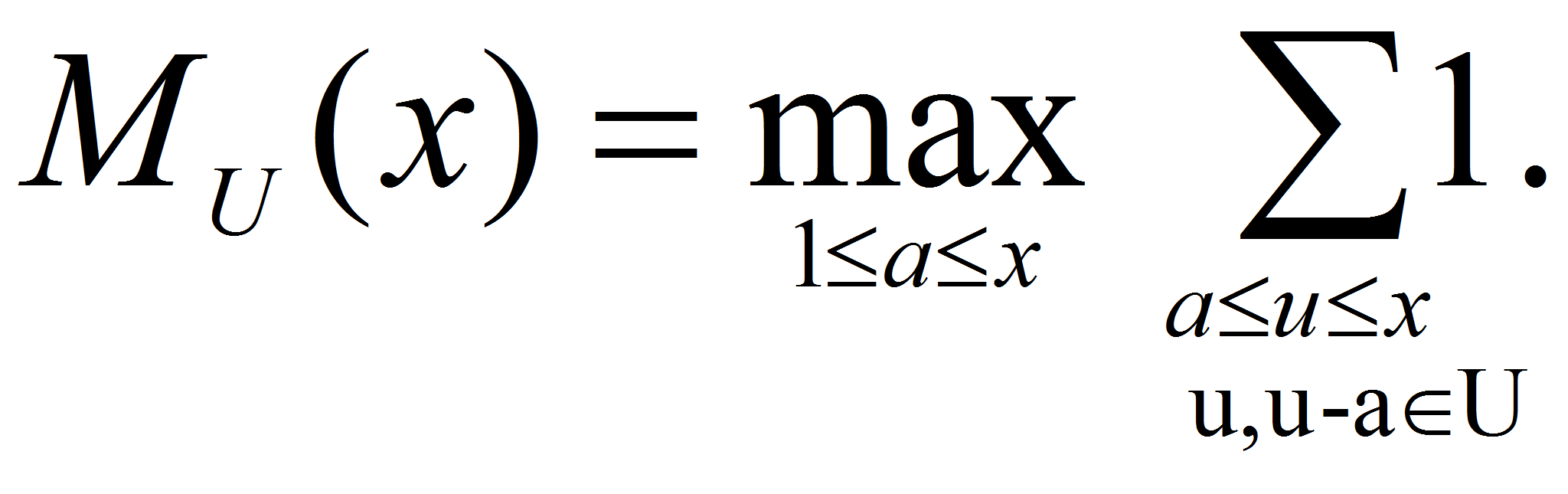Пусть U u
V две последовательности
натуральных чисел,
![]() и
и
![]() их подсчитывающие функции. Введем обозначение
их подсчитывающие функции. Введем обозначение
Доказывается, что при наличии достаточно хорошей оценки MU(x) асимптотическая плотность суммы последовательностей U u V определяется асимптотикой свертки.
Let the u and v are two sequences of natural numbers, where Nu (x) and Nv (x) are their calculating functions. Let us introduce the notation
It is proved that while presence of sufficient positive estimate Mu (x) the asymptotic density of the sum of sequences of u and v is defined by asymptotic compression
Теорема. (Карамата [2]). Пусть f(t) &#;неубывающая функция, определенная для всех t &#;</FONT></I></SPAN><SPAN LANG="sq-AL"><I> 0, f(0) = 0,</I></SPAN><SPAN LANG="sq-AL"><B> <A HREF="images/m4df0c25d.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m4df0c25d.gif" NAME="Объект7" ALIGN=ABSMIDDLE WIDTH=144 HEIGHT=48></A></B></SPAN><B>, </B>причем интеграл сходится при <SPAN LANG="sq-AL"><I>s </I></SPAN><I>> 0</I><B>.</B> Тогда, если по крайней мере одна из функций <SPAN LANG="sq-AL"><I>f(t</I></SPAN><SPAN LANG="sq-AL"><B>)</B></SPAN><SPAN LANG="sq-AL"> </SPAN>или <A HREF="images/m123e443e.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m123e443e.gif" NAME="Объект8" ALIGN=ABSMIDDLE WIDTH=54 HEIGHT=41></A> <FONT FACE="Symbol">&#;</FONT> правильно меняющаяся функция порядка <B><FONT FACE="Symbol">&#;</FONT></B> (в смысле Карамата), то при <I> <A HREF="images/m26710637.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m26710637.gif" NAME="Объект9" ALIGN=ABSMIDDLE WIDTH=44 HEIGHT=18></A> </I> <P><A HREF="images/6bc361dd.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/6bc361dd.gif" NAME="Объект10" ALIGN=ABSMIDDLE WIDTH=161 HEIGHT=41></A>.<P> <I><B>Лемма 1.</B></I> Пусть <SPAN LANG="sq-AL"><I><B>f(t)</B></I></SPAN><SPAN LANG="sq-AL"><I> </I></SPAN><I> и </I><SPAN LANG="sq-AL"><I><B>g(t)</B></I></SPAN><SPAN LANG="sq-AL"><I> </I></SPAN><I><FONT FACE="Symbol">&#;</FONT></I> неубывающие правильно меняющиеся функции порядков соответственно <B><FONT FACE="Symbol">&#;</FONT></B> и <B><FONT FACE="Symbol">&#;</FONT></B>. Тогда при <I> <A HREF="images/m26710637.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m26710637.gif" NAME="Объект11" ALIGN=ABSMIDDLE WIDTH=44 HEIGHT=18></A></I><P> <A HREF="images/m53d4ecad.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m53d4ecad.gif" NAME="Объект12" ALIGN=ABSMIDDLE WIDTH=8 HEIGHT=18></A><A HREF="images/5ca020c3.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/5ca020c3.gif" NAME="Объект13" ALIGN=ABSMIDDLE WIDTH=325 HEIGHT=48></A><P> <I><B>Доказательство.</B></I> Положим <A HREF="images/mae7c5b3.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/mae7c5b3.gif" NAME="Объект14" ALIGN=ABSMIDDLE WIDTH=161 HEIGHT=48></A>; функция <SPAN LANG="sq-AL">h(t) </SPAN> неубывающая, так как <A HREF="images/m7d7e51df.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m7d7e51df.gif" NAME="Объект15" ALIGN=ABSMIDDLE WIDTH=56 HEIGHT=72></A> и <A HREF="images/22daafca.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/22daafca.gif" NAME="Объект16" ALIGN=ABSMIDDLE WIDTH=144 HEIGHT=21></A>.<P> Согласно теореме<I><B> </B></I>Карамата [2], при <I> <A HREF="images/m29400505.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m29400505.gif" NAME="Объект17" ALIGN=ABSMIDDLE WIDTH=44 HEIGHT=18></A></I><P> <A HREF="images/ma51ff9b.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/ma51ff9b.gif" NAME="Объект18" ALIGN=ABSMIDDLE WIDTH=343 HEIGHT=41></A>, <P>откуда следует, что <A HREF="images/m5b76c676.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m5b76c676.gif" NAME="Объект19" ALIGN=ABSMIDDLE WIDTH=52 HEIGHT=41></A><FONT FACE="Symbol">&#;</FONT> правильно меняющаяся функция порядка <I><FONT FACE="Symbol">&#;</FONT></I><I>+</I><I><FONT FACE="Symbol">&#;</FONT></I><I>. </I>Вторично применяя теорему Карамата [2], получаем<DL> <DT> <A HREF="images/m1fb68f0e.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m1fb68f0e.gif" NAME="Объект20" ALIGN=ABSMIDDLE WIDTH=384 HEIGHT=41></A></DL> <P> Пусть <B> </B><SPAN LANG="sq-AL"><I><B>U </B></I></SPAN><I>и</I><SPAN LANG="sq-AL"><I> </I></SPAN><SPAN LANG="sq-AL"><I><B>V</B></I></SPAN> две возрастающие последовательности натуральных чисел<SPAN LANG="sq-AL">, </SPAN><SPAN LANG="sq-AL"><I> <A HREF="images/21a12b35.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/21a12b35.gif" NAME="Объект21" ALIGN=ABSMIDDLE WIDTH=56 HEIGHT=21></A> </I></SPAN><I>и </I><SPAN LANG="sq-AL"><I> <A HREF="images/54f660da.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/54f660da.gif" NAME="Объект22" ALIGN=ABSMIDDLE WIDTH=55 HEIGHT=21></A></I></SPAN><FONT FACE="Symbol">&#;</FONT> их подсчитывающие функции. Введем обозначение<P> <A HREF="images/m30196eb.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m30196eb.gif" NAME="Объект23" ALIGN=ABSMIDDLE WIDTH=58 HEIGHT=69></A><P> <I><B>Теорема 1.</B></I> Имеют место соотношения:<P> <A HREF="images/7ab97798.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/7ab97798.gif" NAME="Объект24" ALIGN=ABSMIDDLE WIDTH=396 HEIGHT=48></A>; (1)<P> <A HREF="images/a86dd0e.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/a86dd0e.gif" NAME="Объект25" ALIGN=ABSMIDDLE WIDTH=405 HEIGHT=48></A> , (2)<P> где <A HREF="images/62f50b63.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/62f50b63.gif" NAME="Объект26" ALIGN=ABSMIDDLE WIDTH=89 HEIGHT=21></A>.<P> <I><B>Доказательство.</B></I> Применим неравенство Романова-Эрдеша к множеству целых точек (<SPAN LANG="sq-AL"><I>u,</I></SPAN><SPAN LANG="sq-AL"><I><FONT FACE="Symbol">&#;</FONT></I></SPAN><SPAN LANG="sq-AL"><I>)</I></SPAN><I>,</I> где <I> <A HREF="images/mf2dea92.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/mf2dea92.gif" NAME="Объект27" ALIGN=ABSMIDDLE WIDTH=167 HEIGHT=18></A>. Т</I>огда<DL> <DT> <A HREF="images/m1c7db77f.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m1c7db77f.gif" NAME="Объект28" ALIGN=ABSMIDDLE WIDTH=196 HEIGHT=84></A> <SPAN LANG="sq-AL">(</SPAN>3<SPAN LANG="sq-AL">) </SPAN> </DL> <P>и <SPAN LANG="sq-AL"> </SPAN> <A HREF="images/29d831d4.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/29d831d4.gif" NAME="Объект29" ALIGN=ABSMIDDLE WIDTH=173 HEIGHT=76></A><SPAN LANG="sq-AL"> (</SPAN>4<SPAN LANG="sq-AL">) </SPAN> <P>Так как <A HREF="images/m321b9038.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m321b9038.gif" NAME="Объект30" ALIGN=ABSMIDDLE WIDTH=140 HEIGHT=21></A>, то отсюда следует<P> <A HREF="images/736f1519.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/736f1519.gif" NAME="Объект31" ALIGN=ABSMIDDLE WIDTH=96 HEIGHT=18></A> <A HREF="images/m6bda4eba.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m6bda4eba.gif" NAME="Объект32" ALIGN=ABSMIDDLE WIDTH=109 HEIGHT=21></A> <A HREF="images/62f50b63.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/62f50b63.gif" NAME="Объект33" ALIGN=ABSMIDDLE WIDTH=89 HEIGHT=21></A><I>.</I><DL> <DT> Заменяя<I> </I><SPAN LANG="sq-AL"><I>P </I></SPAN><I>,</I><SPAN LANG="sq-AL"><I>R</I></SPAN><SPAN LANG="sq-AL"> </SPAN>полученными для них выражениями, получаем формулы (1), (2).</DL> <P> Теорема 1. показывает, что при наличии достаточно хорошей оценки <SPAN LANG="sq-AL"><I>M</I></SPAN><SUB><SPAN LANG="sq-AL"><I>U</I></SPAN></SUB><SPAN LANG="sq-AL"><I>(x)</I></SPAN> асимптотическая плотность суммы последовательностей <SPAN LANG="sq-AL"><I><B>U </B></I></SPAN><I>и</I><SPAN LANG="sq-AL"><I> </I></SPAN><SPAN LANG="sq-AL"><I><B>V</B></I></SPAN> определяется асимптотикой свертки<SPAN LANG="sq-AL"> </SPAN> <A HREF="images/fa5ba37.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/fa5ba37.gif" NAME="Объект34" ALIGN=ABSMIDDLE WIDTH=155 HEIGHT=48></A><P> Большинство последовательностей, рассматриваемых в аддитивной теории чисел, обладает правильно меняющимися подсчитывающими функциями. В этой ситуации из теоремы 1. следует<P> <I><B>Теорема.2.</B></I> Если <SPAN LANG="sq-AL"><I> <A HREF="images/58cc6c76.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/58cc6c76.gif" NAME="Объект35" ALIGN=ABSMIDDLE WIDTH=56 HEIGHT=21></A> </I></SPAN><I>и </I><SPAN LANG="sq-AL"><I> <A HREF="images/m5339a083.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m5339a083.gif" NAME="Объект36" ALIGN=ABSMIDDLE WIDTH=55 HEIGHT=21></A></I></SPAN><FONT FACE="Symbol">&#;</FONT> правильно меняющиеся функции порядков соответственно <I><FONT FACE="Symbol">&#;</FONT></I><B> </B>и<B> </B><I><FONT FACE="Symbol">&#;</FONT></I>, причем<P> <A HREF="images/19b4e671.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/19b4e671.gif" NAME="Объект37" ALIGN=ABSMIDDLE WIDTH=144 HEIGHT=49></A>, (5)<P> то при <A HREF="images/m68aedd6a.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m68aedd6a.gif" NAME="Объект38" ALIGN=ABSMIDDLE WIDTH=48 HEIGHT=18></A><P> <A HREF="images/1ef5bef8.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/1ef5bef8.gif" NAME="Объект39" ALIGN=ABSMIDDLE WIDTH=255 HEIGHT=100></A>. (6)<P> <I><B>Доказательство.</B></I> По лемме 1. в условиях теоремы 2.<P> <A HREF="images/m554b8830.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m554b8830.gif" NAME="Объект40" ALIGN=ABSMIDDLE WIDTH=379 HEIGHT=48></A>. (7)<P> Из условия (5) вытекает<P> <A HREF="images/4b05a263.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/4b05a263.gif" NAME="Объект41" ALIGN=ABSMIDDLE WIDTH=233 HEIGHT=25></A>. (8)<P> Подставляя (7) и (8) в (1) и (2), получаем утверждение теоремы.<P> Таким образом, если <A HREF="images/m7c354ffd.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.orgimages/m7c354ffd.gif" NAME="Объект42" ALIGN=ABSMIDDLE WIDTH=139 HEIGHT=23></A>, то справедливость асимптотической формулы (6) обеспечивается уже просто редкостью последовательности <SPAN LANG="sq-AL"><I><B>V</B></I></SPAN><B>. </B>Арифметическая природа членов этой последовательности не играет никакой роли.<DL> <DT> <DT> Литература:</DL> <OL> <LI><P> Шнирельман Л.Г<B>.</B> Об аддитивных свойствах чисел.<FONT FACE="Symbol">&#;</FONT> Изв. Донского политехнического института,1 ч, 1930, 3<FONT FACE="Symbol">&#;</FONT>28.<LI><P> <SPAN LANG="de-DE">Karamat</SPAN><SPAN LANG="de-DE"><B>a </B></SPAN><SPAN LANG="de-DE">J</SPAN><SPAN LANG="de-DE"><B>. </B></SPAN><SPAN LANG="de-DE">Journal für die reine und angewandt the Mathem. </SPAN><SPAN LANG="en-US">104 (1931), 27</SPAN><SPAN LANG="en-US"><FONT FACE="Symbol">&#;</FONT></SPAN><SPAN LANG="en-US">40</SPAN><LI><P> Барбан М.Б. Метод <FONT FACE="Symbol">&#;</FONT>большего решета<FONT FACE="Symbol">&#;</FONT> и его применения в теории чисел.<FONT FACE="Symbol">&#;</FONT> УМН, 21, 1(1966), 51<FONT FACE="Symbol">&#;</FONT>102<LI><P> Левин Б.В., Файнлейб А.С.<B> </B>Применение некоторых интегральных уравнений к вопросам теории чисел.<FONT FACE="Symbol">&#;</FONT> УМН 22, №3 (35), 1967, 119<FONT FACE="Symbol">&#;</FONT>128. </OL>