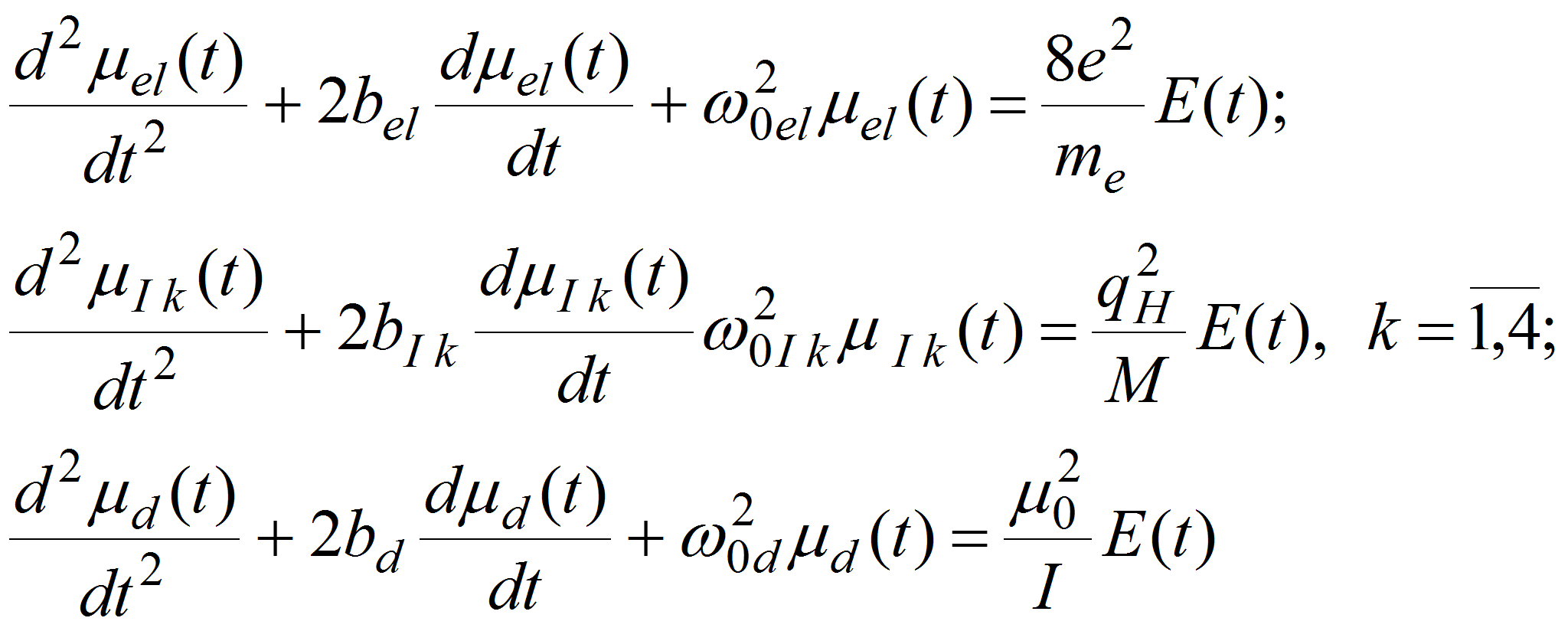Самой распространенной в природе жидкостью, а соответственно и наиболее часто используемым в технике жидким полярным диэлектриком, является вода. При этом ее молекула обладает практически всеми видами упругой деформации заряженных частиц, вызываемой действием слабого электрического поля. Данные обстоятельства определили наличие многочисленных и самых разнообразных экспериментальных данных, позволяющих достоверно оценить адекватность моделей, используемых для описания диэлектрических свойств полярных жидкостей.
Известно, что в рамках классической теории поляризации, явления, происходящие в воде под действием внешнего электрического поля, могут быть представлены следующей системой уравнений [1, с. 67]:
где μel(t), μI k(t) и μd(t) – временные функции, отражающие динамики изменения дипольных моментов, обусловленных соответственно упругой электронной, упругой ионной и дипольной поляризациями молекулы воды; k – индекс разновидностей трансформации химических связей OH (две пары валентных и деформационных колебаний); bel, bI k, bd и &#;0el, &#;</FONT></I></SPAN><SUB>0</SUB><SUB><SPAN LANG="de-DE"><I>I</I></SPAN></SUB><SUB><I> </I></SUB><SUB><SPAN LANG="de-DE"><I>k</I></SPAN></SUB>, <SPAN LANG="en-US"><I><FONT FACE="Symbol">&#;</FONT></I></SPAN><SUB>0</SUB><SUB><SPAN LANG="de-DE"><I>d</I></SPAN></SUB> – динамические параметры уравнений соответствующих процессов; 8<SPAN LANG="en-US"><I>e</I></SPAN><I> </I>– электрический заряд оптической оболочки иона кислорода, заполненной восемью электронами; <SPAN LANG="en-US"><I>m</I></SPAN><SUB><SPAN LANG="en-US"><I>e</I></SPAN></SUB> – масса электрона; <SPAN LANG="en-US"><I>q</I></SPAN><SUB><SPAN LANG="en-US"><I>H</I></SPAN></SUB> – заряд иона водорода;<I> </I><SPAN LANG="en-US"><I>M</I></SPAN><I> </I>– приведенная масса связи <SPAN LANG="en-US"><I>OH</I></SPAN>; <I>μ</I><SUB>0</SUB> и <SPAN LANG="en-US"><I>I</I></SPAN> – собственный дипольный момент и момент инерции молекулы <SPAN LANG="en-US"><I>H</I></SPAN><SUB>2</SUB><SPAN LANG="en-US"><I>O</I></SPAN>.<P> Однако, в данном случае при использовании комплексной диэлектрической проницаемости Борна (2), оказывается то, что<B> </B>она принципиально не учитывает действие электрических полей, возникновение которых имеет место при поляризации ближайшего окружения произвольной молекулы, локализованной в плотной среде, которые существенно влияют на величину эффективного поля, действующего на частицу.<P> <A HREF="894/77d017b8.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.org894/77d017b8.gif" NAME="Объект2" ALIGN=ABSMIDDLE WIDTH=190 HEIGHT=46></A>, (2)<P> Кроме того, использование формулы (2) приводит к появлению так называемой «катастрофы Мосотти», обусловленной наличием отрицательных значений действительной части комплексной диэлектрической проницаемости в области установившихся режимов поляризационных процессов.<P> С целью ликвидации данного обстоятельства за счет уточнения причинно-следственных связей между внешним, деполяризующим и локальным полями, представленными в рамках исходных положений модели Лорентца, проведенного с позиций технической кибернетики, в рамках строгих математических преобразований исходной системы дифференциальных уравнений, описывающих совокупность поляризационных процессов с явным указанием имеющих в них место обратных связей была сформирована «кибернетическую модель» [2, с. 52]:<P> При этом выражение комплексной диэлектрической проницаемости будет иметь вид (3):<P> <A HREF="894/m1dd4ed24.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.org894/m1dd4ed24.gif" NAME="Объект3" ALIGN=ABSMIDDLE WIDTH=197 HEIGHT=46></A>. (3)<P> Принимая во внимание, что общее число электронных пар, имеющихся у молекулы воды, равно пяти, соответствующая динамика процесса упругой электронной поляризации описывается уравнениями (4):<P> <A HREF="894/7bd1763e.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.org894/7bd1763e.gif" NAME="Объект4" ALIGN=ABSMIDDLE WIDTH=371 HEIGHT=94></A> (4)<P> где <I><FONT FACE="Symbol">&#;</FONT></I><SUB><I>k</I></SUB>(<I>t</I>) – наведенные дипольные моменты соответствующих частиц; <I><FONT FACE="Symbol">&#;</FONT></I><SUB>0</SUB><SUB><I>k</I></SUB> и <I>b</I><SUB><I>k</I></SUB> – частоты собственных колебаний и коэффициенты их затухания; <I>e </I>и <I>m</I><SUB><I>e</I></SUB><I> </I>– заряд и масса электрона; <I>E</I><SUB>0</SUB>(<I>t</I>) и <I>E</I>(<I>t</I>) – функции напряженности внешнего и эффективного полей; <I><FONT FACE="Symbol">&#;</FONT></I><SUB>0</SUB> – электрическая постоянная; <I>N</I><SUB><SPAN LANG="en-US"><I>k</I></SPAN></SUB> – концентрации одинаковых частиц. <P>При этом формулы коэффициентов затухания и собственных частот разбираемых колебаний, а также радиальных значений электронных орбит имеют вид (5):<P> <A HREF="894/m77a97093.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.org894/m77a97093.gif" NAME="Объект5" ALIGN=ABSMIDDLE WIDTH=466 HEIGHT=50></A> (5)<P> где <SPAN LANG="en-US"><I>Z</I></SPAN><SUB><I>эф</I></SUB> – эффективный заряд ядра, действующий на электроны оптической оболочки ионов; <I><FONT FACE="Symbol">&#;</FONT></I><SUB>0</SUB> <FONT FACE="Symbol">&#;</FONT> магнитная постоянная; <I>r</I><SUB><I>k</I></SUB> – сферический радиус орбитали; <I>r</I><SUB><I>0</I></SUB> – первый Боровский радиус; <SPAN LANG="en-US"><I>n</I></SPAN> – главное квантовое число электронной оболочки; <I>ћ </I><FONT FACE="Symbol">&#;</FONT> постоянная Планка. <P>Необходимо отметить, что величины <I>Z</I><SUB><I>эф </I></SUB><SUB><SPAN LANG="en-US"><I>k</I></SPAN></SUB> могут рассчитываться на основании методики (6), предложенной Слейтором, согласно которой:<P> – вклад электронов, внешних по отношению к группе <I>X</I> (предполагается, что рассматриваемая орбиталь принадлежит некоторой группе <I>X</I>), равен 0;<P> – вклад электронов из группы <I>X </I>равен 0,30, если это <I>s</I><SUP>1</SUP>-электроны, и 0,35 в остальных случаях;<P> – если рассматриваемые электроны находятся на <I>s</I><SUP><I>k</I></SUP>- или <I>p</I><SUP><I>k</I></SUP>-орбиталях группы <I>X</I>, то вклад каждого из электронов, расположенных на внутренних орбиталях с главным квантовым числом <SPAN LANG="en-US"><I>n</I></SPAN>-1, равен 0,85, а вклады электронов, находящихся на орбиталях с главным квантовым числом <SPAN LANG="en-US"><I>n</I></SPAN>-2,<I> </I><SPAN LANG="en-US"><I>n</I></SPAN>-3, … равны 1,00;<P> – если рассматриваются электроны, расположенные на <I>d</I><SUP><I>k</I></SUP>- или <I>f</I><SUP><I>k</I></SUP>-орбиталях группы <I>X</I>, то вклад каждого из электронов для групп, предшествующих рассматриваемой равны 1,00.<P> <A HREF="894/m2c69a4d5.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.org894/m2c69a4d5.gif" NAME="Объект6" ALIGN=ABSMIDDLE WIDTH=243 HEIGHT=109></A> (6)<P> где <I><FONT FACE="Symbol">&#;</FONT></I><SUB><SPAN LANG="en-US"><I>p</I></SPAN></SUB> – значения экранирующих вкладов для 3<SPAN LANG="en-US"><I>p</I></SPAN>-электронов.<P> Однако, при моделировании графика оптического показателя преломления воды, полученного на базе уравнений (4-6), было обнаружено несоответствие данных физических измерений и расчетного спектра, поэтому авторами было предложено значение <SPAN LANG="en-US">Z</SPAN><SUB>эф</SUB>, объективно характеризующее эффективный заряд атомного остатка, действующий на каждый из электронов иона О<SUP>-2</SUP>, определять по модифицированной методике Слэйтора, в которой значения <I><FONT FACE="Symbol">&#;</FONT></I><SUB><SPAN LANG="en-US"><I>p</I></SPAN></SUB> в трех последних случаях заменяются на истинные экранирующие вклады оптических электронов аниона кислорода, входящего в состав Н<SUB>2</SUB>О, полученные методом сканирования интегральной ошибки между моделируемым и контрольным спектром воды:<P> <A HREF="894/m1a285e3e.gif" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.org894/m1a285e3e.gif" NAME="Объект7" ALIGN=ABSMIDDLE WIDTH=250 HEIGHT=109></A> (7)<P> Результаты имитационного моделирования оптимизированного оптического спектра <SPAN LANG="en-US"><I>n</I></SPAN>(λ) воды изображены на рисунке 1.<P> <A HREF="894/m68bfa737.png" TARGET="_blank"><IMG src="https://articles-static-cdn.moluch.org894/m68bfa737.png" NAME="Графический объект1" ALIGN=BOTTOM WIDTH=402 HEIGHT=332 BORDER=0></A><P> Рис.1. Имитационный оптический спектр воды: точки соответствуют его физическим измерениям [3, с. 39] в области видимых частот<P> <BR /> <P>Проведенное исследование позволяет сформулировать следующие выводы: во-первых, кибернетическое уравнение диэлектрической проницаемости вида (3) является универсальным, так как оно применимо не только к типичной полярной жидкости, но и к диэлектрикам в целом, в частности, к ионным кристаллам. Во-вторых, предложенные математические модели оказываются достаточно эффективными, поскольку позволяют рассчитывать оптические спектры, адекватные их физическим аналогам.<P> <BR /> <P>Литература: <OL><LI><P> Костюков Н.С., Банышева В.В. Поляризационные процессы в воде // Электричество. 2001. № 11. С.66-69.<LI><P> Костюков Н.С., Еремин И.Е. Кибернетическая модель процесса упругой электронной поляризации диэлектрика // Электричество. 2004. №<SPAN LANG="en-US"> </SPAN>1. С.50-54.<LI><P> Золотарев В.М., Морозов В.Н., Смирнова Е.В. Оптические постоянные природных и технических сред: справочник. – Л.: Химия, 1984.</OL>