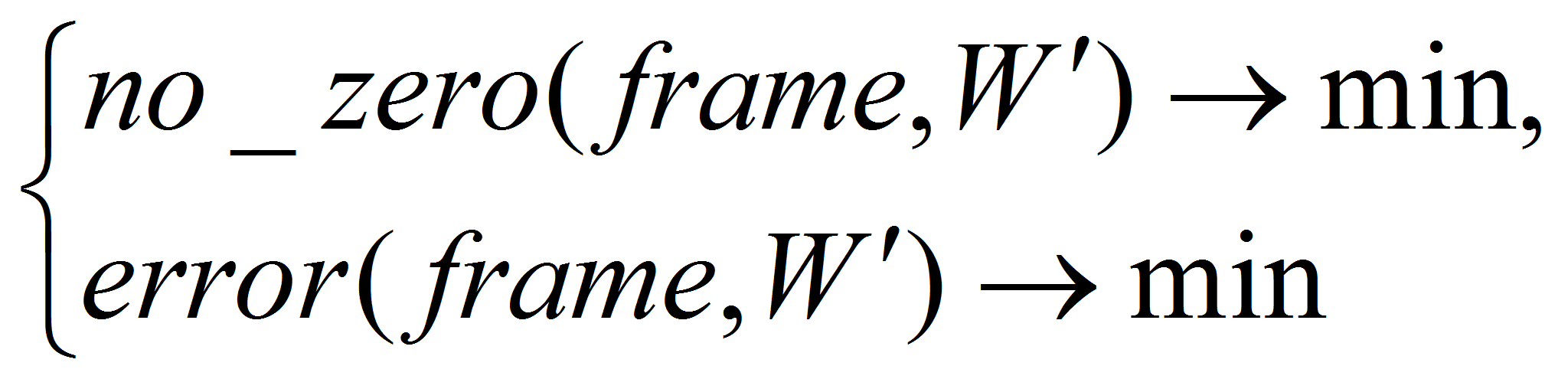Цель работы: поиск оптимального представления речевого сигнала для последующего сжатия с потерями.

Задачи работы: постановка задачи и разработка алгоритма определения оптимального базиса представления речевого сигнала.

Введение.

Постоянное увеличение количества передаваемой по сетям связи мультимедийной информации ставит задачу её оптимального представления и сжатия. Одной из наиболее важных составляющих мультимедийного трафика является аудиоинформация, и, в частности, речевая информация. На сегодняшний день известны следующие методы сжатия речевых сигналов:

1. Кодирование формы сигнала – ИКМ, дельта модуляция, ДИКМ, АДИКМ, субполосное кодирование и т.д.

2. Кодирование параметров речевого сигнала – вокодеры.

3. Гибридное или параметрическое кодирование – полувокодеры.

Данная работа ориентирована на метод кодирования речевого сигнала, основанный на представлении его в адаптивном вейвлет-базисе. В статье предлагается постановка и вариант решения нетривиальной задачи поиска оптимального представления речевого сигнала в указанном базисе.

Исходные данные.

Исходными данными для задачи являются: оцифрованный речевой сигнал и список вейвлетов , где - имя вейвлета, n – количество используемых вейвлетов. Речевой сигнал оцифрован с частотой дискретизации 8кГц и разрядностью отсчетов 16 бит и рассматривается как набор неперекрывающихся кадров длительностью в 128 отсчетов.

Исходя из выбранной длительности кадра в 128 отсчетов, можно предъявить требования к вейвлет-пакетному разложению:

1. количество уровней разложения – 4;
2. размер листьев – 8 отсчетов.

Постановка задачи поиска оптимального вейвлет-пакетного разложения.

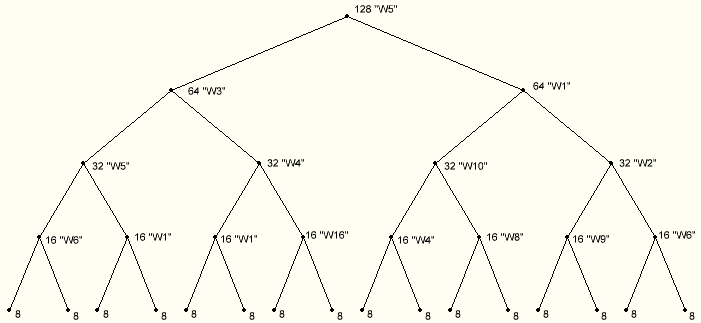
Для поиска оптимального представления из исходного речевого кадра формируется его вейвлет-пакетное разложение. Один из возможных вариантов разложения, соответствующего исходным данным, представлен на рисунке 1. Здесь w_i – i-ый вейвлет из подмножества W’ определенного списка вейвлетов W (), а числа с_k обозначают размерность данных, к которым вейвлет w_i применяется.

Рис. 1. Структура вейвлет-пакетного разложения

Стандартная процедура вейвлет-пакетного разложения описана в [1] и здесь подробно рассматриваться не будет.

Для оценки параметров текущего вейвлет-пакетного разложения для выбранного кадра речи frame, и заданного списка используемых вейвлетов (при рассмотрении процедуры вейвлет-пакетного разложения не имеет значения способ выбора , т.к. это общая процедура и применима к любому ) выполняем следующую процедуру:

1. формируем вейвлет-пакетное разложение кадра frame в выбранном базисе ;
2. для всех листьев полученного вейвлет-пакетного разложения определяем значение энтропии Шеннона 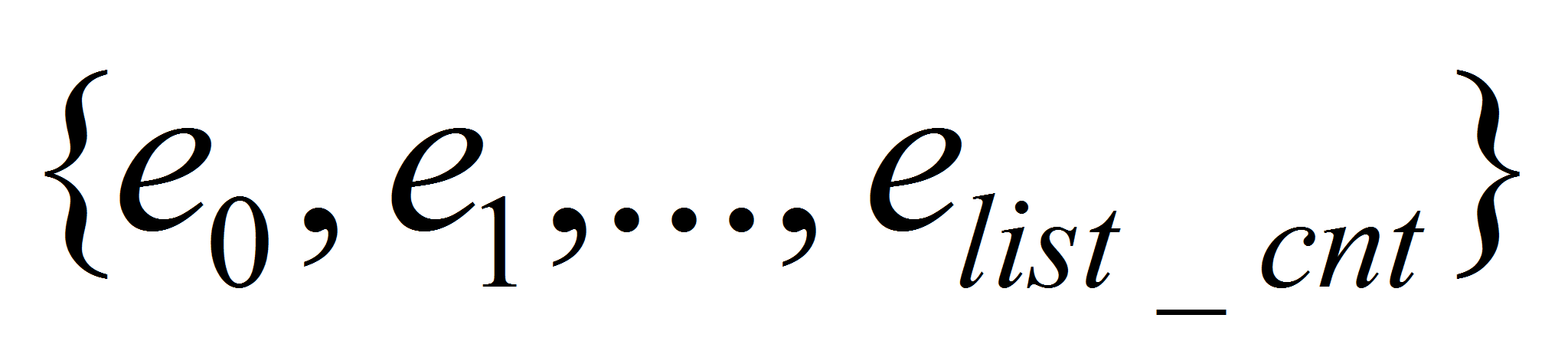, где list_cnt – количество листьев вейвлет-пакетного разложения;
3. определяем среднее значение энтропии по всем листьям разложения
   
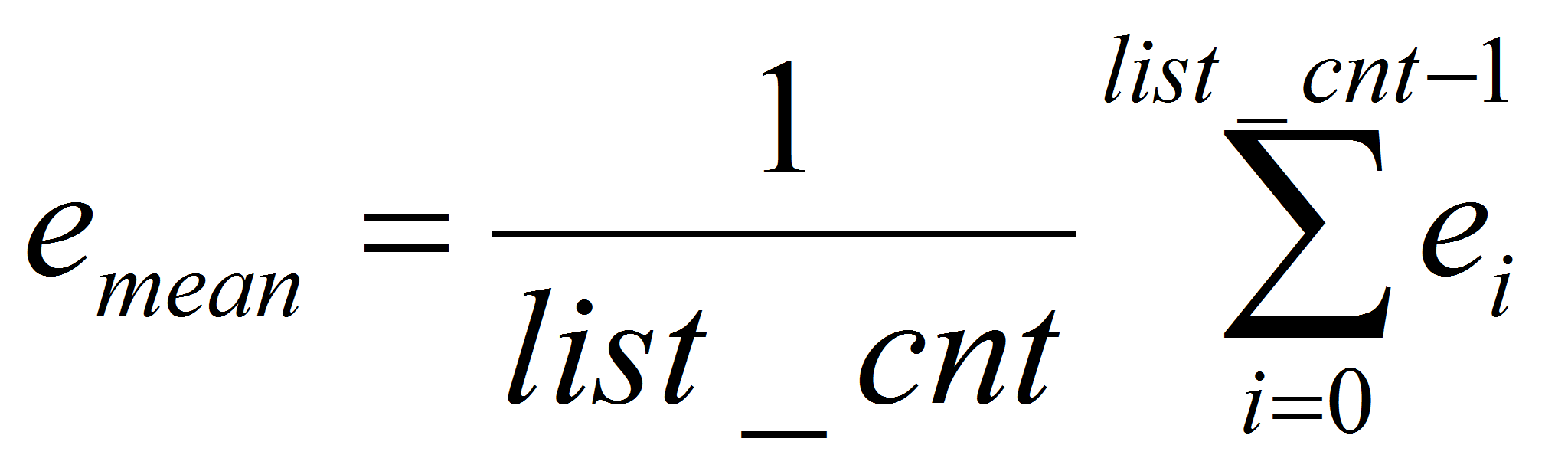
4. листья со значением энтропии меньше средней заменяем листьями с нулевыми значениями вейвлет-коэффициентов;
5. определяем количество ненулевых листьев – обозначим его ;
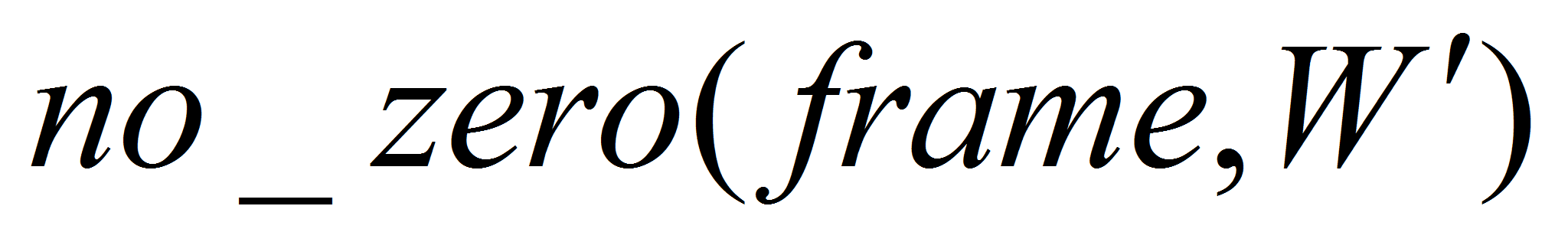6. восстанавливаем сигнал, проведя процедуру обратного вейвлет-пакетного разложения; полученный сигнал обозначим ;
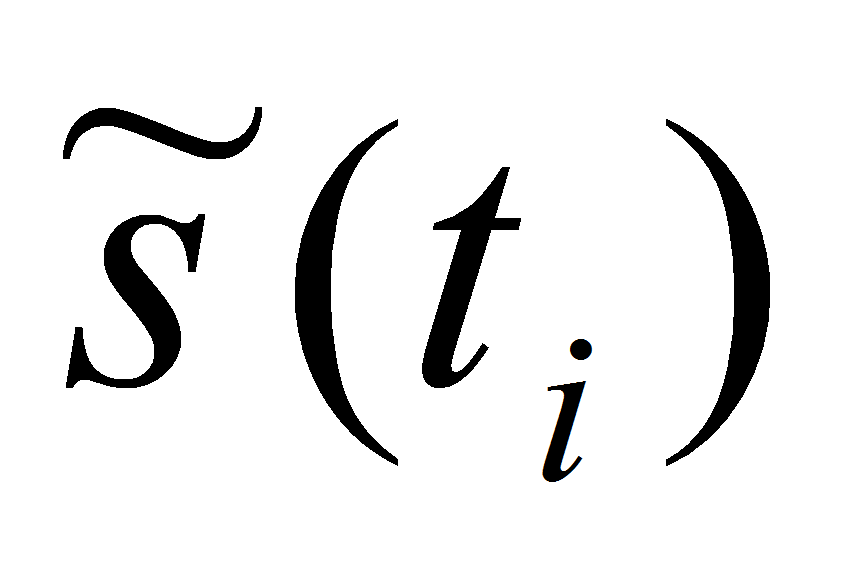7. оцениваем среднеквадратическую разность исходного и восстановленного сигналов
   ,
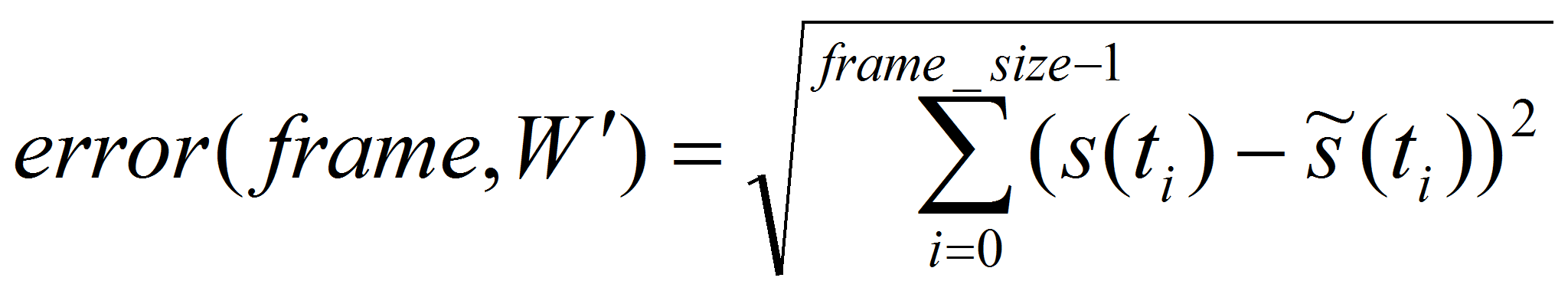   где frame_size – размер рассматриваемого кадра.

Представленная процедура для каждого кадра frame и текущего списка используемых вейвлетов формирует характеризующие эту пару параметры:

1. количество ненулевых листьев – ;
2. коэффициент линейных искажений – ;

Для поиска оптимального разложения указанные параметры можно использовать при постановке следующей задачи оптимизации: найти такое подмножество множества вейвлетов , для которого

, (1)

Составляем целевую функцию следующим образом:

, (2)

где a и b – имеют смысл некоторых нормировочных коэффициентов. Выбор вида целевой функции обусловлен её гладкостью в пространстве no_zero – error.

Тогда задачу (1) можно переформулировать как задачу поиска такого разложения _, для которого:

, (3)

В таком виде и будем решать задачу поиска оптимального вейвлет-представления речевого сигнала.

Формирование списка вейвлетов.

Длительность исходного сигнала и количество уровней разложения (см. исходные данные) накладывает определенные ограничения на типы используемых вейвлетов, а именно – количество коэффициентов вейвлета не может превосходить 16, иначе невозможно получение 4-го уровня разложения. Таким образом, можно определиться с составом списка вейвлетов и их количеством.

Задача определения коэффициентов вейвлета высокого порядка сопряжена со значительными вычислительными трудностями (решение системы нелинейных уравнений высокого порядка), поэтому в своей задаче будем использовать известные вейвлеты, определенные в Wavelet toolbox – пакете расширения MATLAB.

Учитывая указанные ограничения на вейвлеты, получаем список вейвлетов применимый к нашей задаче (список сформирован по группам):

1) вейвлеты Добеши: db1, db2, db3, db4, db5, db6, db7, db8;

2) койфлеты: coif1, coif2;

3) симплеты: sym2, sym3, sym4, sym5, sym6, sym7, sym8;

4) биортогональные вейвлеты: bior1.3, bior1.5, bior2.2, bior2.4, bior2.6, bior3.1, bior3.3, bior3.5, bior3.7, bior4.4, bior5.5;

5) обратные биортогональные вейвлеты: rbio1.3, rbio1.5, rbio2.2, rbio2.4, rbio2.6, rbio3.1, rbio3.3, rbio3.5, rbio3.7, rbio4.4, rbio5.5.

Общее количество возможных вейвлетов составляет 38. Таким образом, общее количество возможных деревьев вейвлет-пакетного разложения одного кадра речевого сигнала составляет .

Вариант решения задачи поиска оптимального вейвлет-пакетного разложения.

В виду очень большого количества возможных вариантов представления исходного кадра вейвлет-пакетным разложением, применение классических методов оптимизации представляется маловозможным. Одним из возможных методов сокращения перебора может быть использование эвристических алгоритмов, а точнее генетического алгоритма [3]. Генетические алгоритмы хорошо зарекомендовали себя в задачах комбинаторной оптимизации [2, 4] (задача коммивояжера, раскраска, нахождение паросочетаний), теории расписаний [2] и т.д.

Рассмотрим, кратко, функционирование генетического алгоритма.

1. инициализируем начальную популяцию особей, случайным образом;
2. для каждой особи популяции вычисляем её приспособленность (fitness);
3. выполняем операции селекции, позволяющие выбрать наиболее приспособленные особи популяции; возможно несколько вариантов операции селекции: колесо рулетки, турнирная, с частичной заменой популяции и т.д.;
4. с определенной вероятностью выполняем операцию скрещивания (кроссовера) над полученной популяцией; возможно несколько вариантов выполнения скрещивания – точечное, блочное и т.д.;
5. с определенной вероятностью выполняем операторы мутации; возможные виды мутации: циклический сдвиг, обмен генов, инверсия и т.д. (после выполнения этого шага имеем новую популяцию);
6. выполняем проверку условия завершения алгоритма; при выполнении условия переходим к шагу 8;
7. выполняем инкремент номера популяции и переходим к шагу 2;
8. завершаем работу алгоритма.

В нашем исследовании функцией приспособленности будет являться целевая функция (2), в качестве операции селекции – турнирная селекция, операторы скрещивания и мутации – принципиального значения не имеют. Условием завершения будет превышение алгоритмом заданного количества итераций, это позволит избежать зацикливания алгоритма.

Заключение.

В статье поставлена задача на исследование и частично указанны методы исследования. Анализ данных, которые будут получены в результате исследования, даст обширную информацию о возможности применения вейвлет-пакетного разложения к задаче оптимального представления и сжатия речевого сигнала. По результатам исследования будет принято решение о программной реализации кодека речевых сигналов в адаптивном вейвлет-базисе.

Литература:

1. Смоленцев Н.К. Основы теории вейвлетов. Вейвлеты в MatLAB. – М.:ДМК Пресс, 2008. – 448с.: ил. ISBN 5-94074-415-X
2. Лю Б. Теория и практика неопределенного программирования. – М.:БИНОМ. Лаборатория знаний, 2005. – 416c.:ил. ISBN 5-94774-241-1
3. Панченко Т.В. Генетические алгоритмы: учебно-методическое пособие. – Астрахань: Издательский дом “Астраханский университет”, 2007. – 87c. ISBN 5-88200-913-8
4. Steeb W. The nonlinear workbook – World Scientific Publishing Co. Pte. Ltd, 2001. – 597p. ISBN 981-02-4025-2