Решена задача управления дебитом жидкости. Процесс описывается гиперболическим уравнением с начально-краевыми условиями. Процесс управляется давлением или дебитом газа на башмаке. Найдена управляющая функция, зависящая от времени. Найдены точки оптимума дебита для нефтяных и газовых скважин.
Ключевые слова:газлифт, дебит нефти, дебит газа, давление, закачиваемый расход газа.
Problem of liquid yield control was solved. The process is described by a hyperbolic equation with initial-boundary conditions. The process is controlled by pressure or gas yield on the shoe. A time dependent control function was found. Optimum yield points for oil and gas wells were found.
Key words: gas lift, oil flow rate, gas flow rate, pressure, injected gas flow rate.
В статье решены задачи достижение оптимального дебита с учетом предельного градиента давления нефти управляя минимальной энергией давлением на башмаке.
Пусть начало координатной системы находится в верхней точке насосно-компрессорной трубы (НКТ) и ось ![]() направлена вниз по центру окружности поперечного сечения НКТ.
направлена вниз по центру окружности поперечного сечения НКТ.
Неустановившееся движение изотермической газожидкостной среды в вертикальной трубе длиной ![]() и постоянным поперечным сечением
и постоянным поперечным сечением ![]() НКТ описывается следующим дифференциальным уравнением в частных производных [1,2]:
НКТ описывается следующим дифференциальным уравнением в частных производных [1,2]:
![]() +
+![]() +
+![]() ,
,
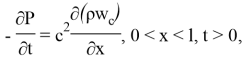
где ![]() перепад давления стационарной и возмущенной газожидкостной среды,
перепад давления стационарной и возмущенной газожидкостной среды, ![]() средняя скорость смеси по трубе вверх,
средняя скорость смеси по трубе вверх,
![]() — скорость звука в жидкости,
— скорость звука в жидкости, ![]() коэффициент гидравлическог сопротивления,
коэффициент гидравлическог сопротивления, ![]() плотность смеси, число слагаемых равно числу фаз,
плотность смеси, число слагаемых равно числу фаз, ![]() — ускорение силы тяжести,
— ускорение силы тяжести, ![]() диаметр поперечного сечения,
диаметр поперечного сечения, ![]() предельный градиент давления. Не ограничивая общности можно положить
предельный градиент давления. Не ограничивая общности можно положить ![]()
Решим следующую задачу оптимального управления: При ![]() т. е. чтобы перевести систему за время
т. е. чтобы перевести систему за время ![]() в состояние
в состояние
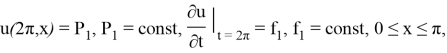
нужно найти управление ![]() при этом
при этом
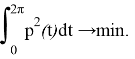
Решая задачу, найдем оптимальную управляющую функцию в следующем виде
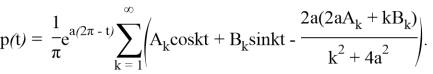
Итак, решение задачи будет
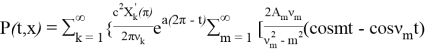 +
+
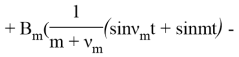
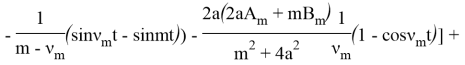
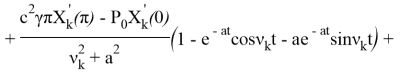
![]() +
+![]() ,
,
где ![]()
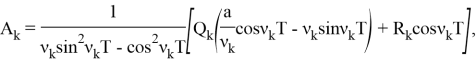
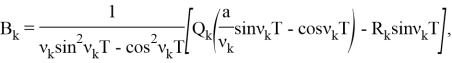
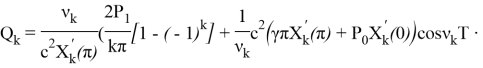
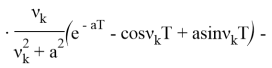
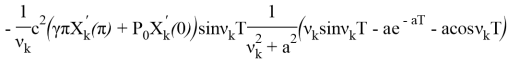
![]()
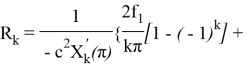
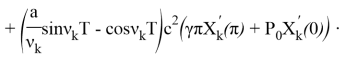
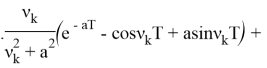
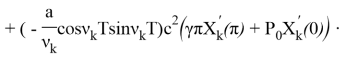
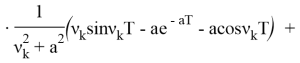
![]()
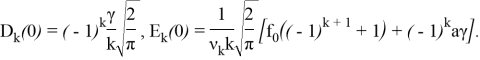
В этой задаче для следующих исходных данных проведены вычисления с использованием математического пакета Maple:
![]()
![]() ;
;![]()
![]() ,
, ![]()
Для нефтяных и газовых компаний имеет практическое значение предварительное теоретическое решение задач по добыче нефти и газа. Эти задачи рассмотрены в [1] без учета предельного градиента давления нефти.
Выводы
-
При создании на устье скважины 70 atm с помощью найденной управляющей функции начинается движение газожидкостной смеси в насосно-компрессорной трубе. При
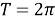 процесс переводится в стационарное состояние. При этом вычислено, что можно добыть нефти за сутки в оптимальном режиме 69,4 т., а максимальном режиме — 80,2 т.
процесс переводится в стационарное состояние. При этом вычислено, что можно добыть нефти за сутки в оптимальном режиме 69,4 т., а максимальном режиме — 80,2 т.
- Полученные численные результаты совпадают с ранее известными промысловыми статистическими данными, а также они показывают на практическую пользу применение теории оптимального управления к нефтедобыче и может служить руководством для нефтянников и газовиков.
Литература:
- Алиев, Ф.А., Ильясов, М.Х., Нуриев, Н. Б. Проблемы математического моделирования, оптимизации и управления газлифта. Доклады НАН Азербайджана, 2009, № 2, с.43–57.
- Мирзаджанзаде, А.Х., Аметов, И.М., Хасанов, А. М. Технология и техника добычи нефти. М.: Недра, 1986. 382 с.

