В работе описывается реализация методов регулирования скорости вращения асинхронного двигателя. Данная тема является актуальной в связи с тем, что в настоящее время настройка параметров системы регулирования скорости вращения асинхронного двигателя является сложной задачей, требующей больших затрат времени на подбор коэффициентов.

Ключевые слова: регулирование скорости вращения, ПИД-регулятор, асинхронный двигатель, автоподбор коэффициентов, алгоритмы, программная реализация.

Регулирование скорости вращения мощного асинхронного двигателя при переменной нагрузке является сложной задачей. Для этого чаще всего используют ПИД-регуляторы. Использование ПИД-регуляторов помогает уменьшить энергетические потери на настройку системы и обеспечивает более быстрый выход на требуемые параметры.

Для эффективной работы регулятора в процессе работы необходимо правильно подбирать его коэффициенты и изменять их при изменении внешних условий. В связи с этим возникает необходимость в разработке программного обеспечения для реализации математических методов настройки регулятора.

В реализованном методе расчёта выходного сигнала U [n] через промежутки времени, равные периоду дискретизации T, в моменты времени n  T используется формула

(1)

гдеn — номер текущего периода дискретизации;

_n и _{n — 1} — текущая и предыдущая ошибка рассогласования соответственно;

K_p, K_i, K_d — пропорциональный, интегральный и дифференциальный коэффициенты ПИД-регулятора.

Ошибка рассогласования _n рассчитывается по формуле

_n = y_{n —} y_зад,(2)

где y_n – выходное значение регулятора; y_зад — заданное входное значение (уставка).

В процессе реализации регуляторов часто возникает ситуация, когда нет возможности точно поддерживать одинаковый период дискретизации при программном управлении. В этом случае сильно ухудшается качество управления, так как в процессе расчета выходного сигнала не учитывается неравномерность периода дискретизации. Это приводит к появлению такой проблемы, как неверное вычисление значения выходного сигнала на текущем шаге. В этом случае следует выполнить переход к описанию коэффициентов регулятора через постоянные времени интегрирования T_i и дифференцирования T_d:

(3)

(4)

гдеT — период дискретизации.

Окончательно формула для расчета выходного сигнала цифрового регулятора U [n] примет вид:

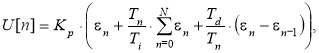(5)

гдеn — номер текущего периода дискретизации;

T_n — период дискретизации на текущем шаге;

, — время запуска функции регулятора на текущем и предыдущем шаге;

T_i — постоянная времени интегрирования;

T_d — постоянная времени дифференцирования.

K_{p —} пропорциональный коэффициент ПИД-регулятора.

Период дискретизации на текущем шаге определяется по формуле

(6)

Данный переход полностью устраняет обозначенную выше проблему ухудшения качества регулирования, так как в нем учитывается время, прошедшее с момента предыдущего расчета выходного сигнала.

В целях адаптации классического алгоритма расчета коэффициентов к решаемой задаче был разработан и реализован модифицированный программный ПИД-регулятор. Алгоритм функции расчёта коэффициентов для классического ПИД-регулятора представлен на рис. 1,а, для метода модифицированного ПИД-регулятора — на рис. 1,б.

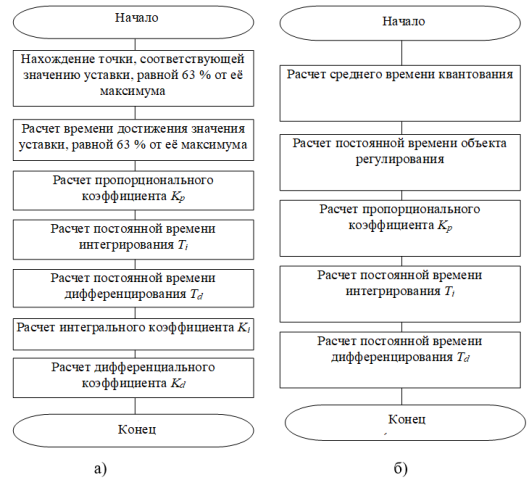
Рис. 1. Алгоритм расчета коэффициентов для ПИД-регулятора: а) классического; б) модифицированного

Ниже приведен текст подпрограммы для реализации регулятора.

Проведенные на стенде испытания показали работоспособность предложенного алгоритма и его программной реализации.

Литература:

1. ПИД-регулятор. [Электронный ресурс]. URL: https://ru.wikipedia.org/wiki/ПИД-регулятор (дата обращения 20.04.1019).
2. Назначение регуляторов. [Электронный ресурс]. URL:
3. https://elektronchic.ru/avtomatika/pid-regulyator-polnoe-opisanie-primenenie.html (дата обращения 20.04.1019).
4. Сазонов А. А. Микропроцессорное управление технологическим оборудованием микроэлектроники: учеб. пособие / А. А. Сазонов. — М.: Радио и связь, 1998. — 264 с.
5. Радионов В. Д. Технические средства АСУ ТП: учеб. пособие для вузов /В. Д. Радионов. — М.: Высшая школа, 1989. — 263 с.