Основными процессами, определяющими долговечность и надежность различных конструкций, являются процессы изгибных колебаний и усталости.
Факторы, которые влияют на процесс усталости, в докладе представлены в виде параметров, учитывающих геометрические размеры конструкции мостового металлургического крана, температурный режим работы, прочностные свойства и комбинированный характер нагружения.
К внешним нагрузкам относятся действующие нагрузки при каждом технологическом цикле (подъем груза — транспортирование груза — опускание груза).
Предложен метод преобразования вероятностей входных и выходных параметров рассматриваемой механической системы.
Полученные теоретические выражения позволяют производить расчеты надежности металлургических мостовых кранов и с определенным уровнем допущения оценивать риски, связанные с эксплуатацией таких конструкций.
Ключевые слова: надежность, долговечность, усталость, метод преобразования вероятностей, входные и выходные параметры, механическая система, конструкция, статистические характеристики
Оценка техногенной безопасности представляет собой достаточно насущную и актуальную проблему. Эта проблема требует новых подходов [1, 3, 4].
При решении прикладной задачи синтеза механической системы мостового крана будем рассматривать процессы, одновременно протекающие в рассматриваемых элементах и определяющих срок службы всей системы. Основными процессами, определяющими долговечность и надежность рассматриваемой системы, будут процессы изгибных колебаний и усталости.
Факторы, влияющие на процесс усталости в материале расчетной динамической системы, представим в виде нескольких параметров [1–8]: ![]() ,
,![]() факторы, определяющие соотношение между геометрическими размерами фермы крана, температурный режим работы, прочностные свойства материала и комбинированный характер нагружения, в совокупности влияющие на величину числа циклов до выхода из строя конструкции по усталости:
факторы, определяющие соотношение между геометрическими размерами фермы крана, температурный режим работы, прочностные свойства материала и комбинированный характер нагружения, в совокупности влияющие на величину числа циклов до выхода из строя конструкции по усталости:
![]()
![]()
![]() (1)
(1)
![]()
![]()
К внешним параметрам системы отнесем нагрузки, которые действуют на ферму и элементы крана. Они определяют входные параметры системы, случайным образом воздействующие на нее в виде случайного процесса входа системы. Следовательно, выходные параметры — это число циклов до выхода из строя по усталости, представляют реакцию системы на действие внешних и внутренних входных факторов, а также являющиеся определяющим параметром надежности конструкций и в частности мостовых металлургических кранов.
Представим функциональную зависимость между входными и выходными параметрами системы в следующем виде:
![]() (2)
(2)
где ![]() A — параметр, зависящий от (1), определяется экспериментально; ky – постоянный коэффициент; Ny – число циклов до выхода из строя по усталости; my, ny – показатели степени, определяемые экспериментально; Рд – сила, действующая на конструкцию фермы и механизм подъема крана.
A — параметр, зависящий от (1), определяется экспериментально; ky – постоянный коэффициент; Ny – число циклов до выхода из строя по усталости; my, ny – показатели степени, определяемые экспериментально; Рд – сила, действующая на конструкцию фермы и механизм подъема крана.
Решив уравнение (2) относительно ![]() , представим выражение статистической динамики с учетом [2, 5, 6] в виде:
, представим выражение статистической динамики с учетом [2, 5, 6] в виде:
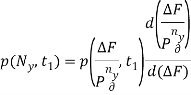 (3)
(3)
которая представляет собой плотность вероятности выходного параметра системы – числа циклов до выхода из строя по усталости.
При условии независимости входных параметров по нормальному закону распределения получим функцию![]() после решения и преобразований уравнения (3):
после решения и преобразований уравнения (3):
![]() =
= 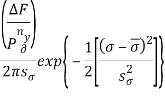 (4)
(4)
где ![]() – среднее значение изгибных напряжений,
– среднее значение изгибных напряжений, ![]() – среднеквадратическое отклонение изгибных напряжений.
– среднеквадратическое отклонение изгибных напряжений.
Располагая опытными или эксплуатационными данными о предельных величинах действующих нагрузок и построив кривую плотности вероятности ![]() , можно судить о возможных величинах выходных параметров для режима нагружения и требуемого срока эксплуатации. Это можно установить также при наличии статистических характеристик распределения – математического ожидания M[
, можно судить о возможных величинах выходных параметров для режима нагружения и требуемого срока эксплуатации. Это можно установить также при наличии статистических характеристик распределения – математического ожидания M[![]() ] и дисперсии D[
] и дисперсии D[![]() ], которые определяются следующими выражениями:
], которые определяются следующими выражениями:
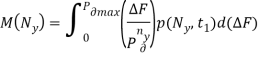 (5)
(5)
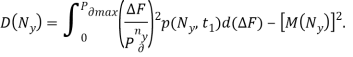 (6)
(6)
Расчет проводился в известных математических пакетах и дал удовлетворительные результаты, согласующиеся с теоретическими и эксплуатационными параметрами рассматриваемых элементов конструкций.
Полученные теоретические выражения позволяют производить расчеты надежности металлургических мостовых кранов и с определенным уровнем допущения оценивать риски, связанные с эксплуатацией таких конструкций. В отличие от ранее предложенных расчетов [4, 6] данный расчет учитывает большее количество входных параметров, что соответственно повышает информативность рассматриваемого подхода к проблеме.
Таким образом, можно провести расчеты и построить нормы рисков для определенного класса оборудования. Это позволит существенно влиять на обеспечение техногенной безопасности и управление ею, прогнозировать изменение механических характеристик материала конструкции на всех этапах жизненного цикла.
Литература:
1. Бархоткин В. В., Извеков Ю. А., Миникаев С. Р. Обзор аварий на крановом оборудовании металлургических производств. // Международный журнал прикладных и фундаментальных исследований. — Москва, РАЕ, 2013. — № 10–1. С. 9–11.
2. Бирюков М. П. Динамика и прогнозирующий расчет механических систем. // «Вышэйшая школа». — Минск, 1980. — 189 с: ил.
3. Извеков Ю. А. Анализ техногенной безопасности кранового хозяйства России. // Современные наукоемкие технологии. — Москва, РАЕ, 2012. — № 12. С. 18–19.
4. Извеков Ю. А. Прогнозирование надежности несущих конструкций кранов металлургических производств. Вопросы. Гипотезы. Ответы: Наука XXI века: Коллективная монография. — Краснодар, 2013. Книга 6, часть 3, глава 9. С. 189–211.
5. Izvekov Y. A., Dubrovsky V. V., Hamutskikh E. Y. Mathematical Modeling and Calculation of Accuracy and Durability of Mechanical Systems' Elements. // World Applied Sciences Journal 30 (1): pp. 32–34, 2014.
6. Извеков Ю. А. Вероятностный синтез сложной механической системы. // Молодой ученый. — 2014. — № 4. — С. 179–182.
7. Izvekov Y. A., Kobelkova E. V., Loseva N. A. Numerical calculation of durability and reliability using correlation method. Life Science Journal, 2014. № 11(8s), pp. 272–274.
8. Извеков Ю. А., Грачева Л. А. Анализ научно-методического аппарата и современных подходов к оценке безопасности сложных технических систем. // Международный журнал прикладных и фундаментальных исследований. — 2014. — № 8 — стр. 9–10.

