В статье рассмотрен случай, когда сигнал известной формы передается на фоне последовательности со сложной структурой. При этом синтезирован алгоритм обнаружения такого сигнала. Проведено исследование эффективности обнаружения для двух типов моделей.

Ключевые слова: дважды стохастические модели, имитация случайных процессов, обнаружение сигналов

Важнейшая задача статистической радиотехники — несомненно задача обнаружения сигналов [3–4]. Вся современная радиолокация происходит из попыток решить данную задачу. Действительно, обнаружение какой-либо цели может привести к благоприятным результатам в борьбе с противником или минимизировать собственные затраты. При этом при проектировании обнаружителей важно иметь какую-либо статистику. Эти данные можно получить с помощью статистического моделирования. Для описания сложных изображений себя хорошо зарекомендовали дважды стохастические модели [1,2,5,6].

Когда происходит обнаружение сигналов на фоне помех с авторегрессионной или дважды стохастической структурой, то имеются гипотезы о наличии детерминированного сигнала , на интервале дискретного времени (рис. 1) (гипотеза ) и гипотеза об отсутствии сигнала на интервале (гипотеза ). Запишем наблюдения как смесь реализации дважды стохастического процесса и белого шума, а также сигнала в соответствующей области:

,

,

где − случайные величины (СВ) с изменяющимися корреляционными связями ; − независимые гауссовские СВ с нулевыми средними значениями и дисперсиями (в случае, когда дисперсии постоянны). При отсутствии детерминированного сигнала (гипотеза ) наблюдения представляют собой сумму коррелированной помехи и белого шума: .

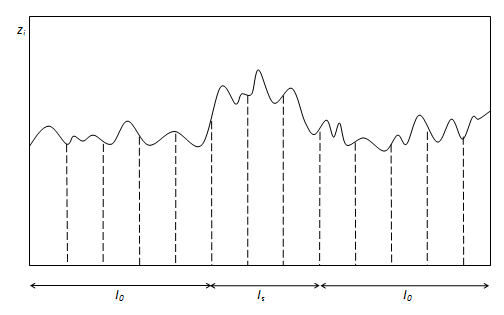
Рис. 1. Наблюдение сигнала на фоне коррелированной помехи

Для решения задачи обнаружения имеем следующую статистику:

.

Чтобы принять решение, есть ли сигнал или нет, необходимо найти и сравнить с пороговым уровнем:

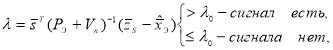(1)

где находится, например, из условия обеспечения заданной вероятности ложной тревоги .

Для того, чтобы получить статистику (1), воспользуемся известным выражением связи между прогнозом и оценкой вектора :

,

где − ковариационная матрица ошибок оптимального оценивания: . После подстановки этих соотношений в (1), получим

.(2)

Запишем вероятности ложной тревоги и пропуска цели следующим образом

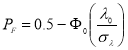- вероятность ложной тревоги,

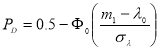— вероятность пропуска цели,

где — функция Лапласа, , .

Соответственно для вычисления вероятности правильного обнаружения нужно из единицы вычесть вероятность пропуска цели. Пороговое значение находится из условия, что выбирается заданная вероятность ложной тревоги.

Найдем необходимые статистические характеристики:

,

.

Таким образом, вычисление статистики (2), а также статистических характеристик требует проведения предварительного оценивания полезного сигнала.

Было проведено статистическое моделирование, при котором сравнивались дважды стохастическая и авторегрессионная модели.

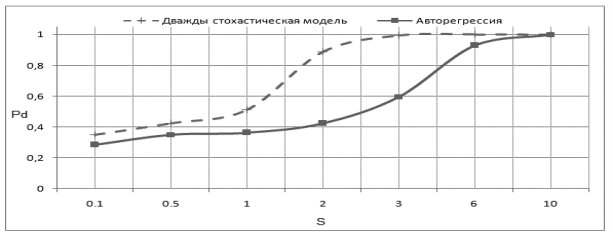
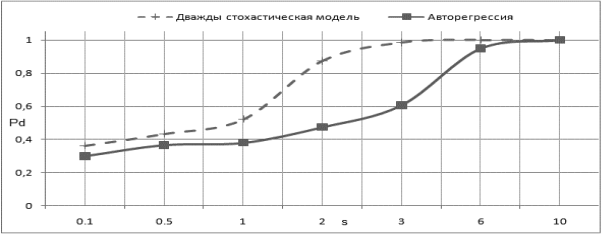
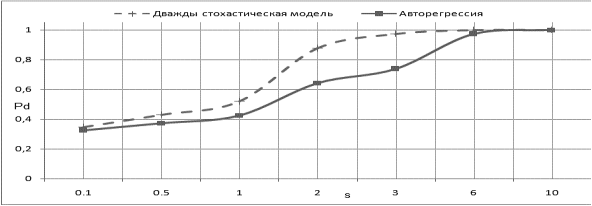
Зависимость эффективности обнаружения сигнала от уровня сигнала и при разных параметрах r показана на рис. 2.

а

б

в

Рис. 2. Вероятность правильного обнаружения сигнала на основе дважды стохастической (штриховая линия) и авторегрессионной (сплошная линия) моделей: а — r = 0.3, б — r = 0.8; в — r = 0.99.

Очевидно, что дважды стохастическая модель обеспечивает эффективность обнаружения протяженных сигналов на 20–30 % выше, чем авторегрессионная. Следовательно, ее использование при проектировании реальных сигнал будет целесообразнее.

Литература:

1. Андриянов Н. А. Дискретные дважды стохастические авторегрессионные модели случайных полей // Современные проблемы проектирования, производства и эксплуатации радиотехнических систем. 2014. № 1 (9). С. 69–72.
2. Vasil'ev K. K., Dement'ev V. E., Andriyanov N. A. Application of mixed models for solving the problem on restoring and estimating image parameters // Pattern Recognition and Image Analysis (Advances in Mathematical Theory and Applications). 2016. Т. 26. № 1. С. 240–247.
3. Васильев К. К., Балабанов В. В. Обнаружение точечных аномалий на фоне мешающих изображений // Радиотехника. 1991. № 10. С. 86.
4. Васильев К. К., Павлыгин Э. Д., Гуторов А.С Многомодельные алгоритмы обработки данных системы мобильных РЛС // Автоматизация процессов управления. 2014. № 4 (38). С. 4–13.
5. Андриянов Н. А. Величина ошибки прогноза в точку на фоне смешанной модели сигнала // Современное научное знание: теория, методология, практика Сборник научных трудов по материалам Международной научно-практической конференции в 3-х частях. ООО «НОВАЛЕНСО». Смоленск, 2016. Ч. 3, С. 34–36.
6. Андриянов Н. А., Васильев К. К., Дементьев В. Е. Разработка программного комплекса для решения задач фильтрации случайных полей // Современные тенденции в науке, технике, образовании. Сборник научных трудов по материалам Международной научно-практической конференции: в 3-х частях. 2016. Ч. 1, С. 40–41.