В статье приведена линеаризованная структурная схема системы ПЧ-АД. Дается математическое описание замкнутой системы управления ПЧ-АД, и программа расчета фазовой траектории системы.

Ключевые слова: линеаризированная система, фазовая траектория, преобразователь частоты, асинхронный двигатель.

The linearized block diagram of system of PCh — the HELL is provided in article. The mathematical description of the closed PCh-AD control system, and the program of calculation of a phase trajectory of system is given.

Keywords: linearizirovnny system, phase trayektoriya, frequency converter, asynchronous engine.

Требование устойчивости переходных процессов системы автоматического управления является основным условием нормального функционирования системы управления [1]. Для нелинейных систем управления нет единого точного метода решения нелинейных уравнений, описывающие переходные процессы системы и для каждого вида нелинейности приходится изыскивать специфический частный метод [2]. Для определения устойчивости замкнутой системы «Преобразователь частоты — асинхронный двигатель» (ПЧ-АД) выбран метод фазового пространства [3]. Данный метод позволяет получить наглядную картину переходных процессов системы автоматического управления и по фазовым траекториям определять устойчивость системы управления. Структурная схема замкнутой системы ПЧ-АД с нелинейным статическим звеном в MATLAB представлено на рисунке 1.

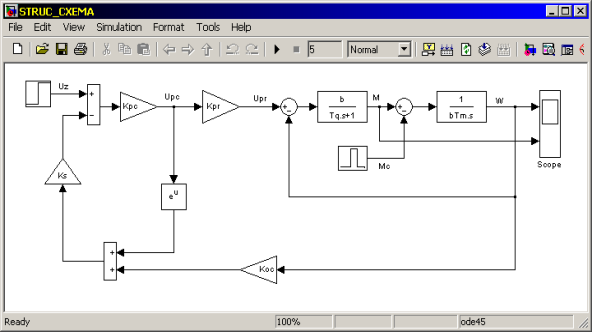
Рис. 1. Структурная схема замкнутой системы ПЧ-АД

Структурная схема асинхронного двигателя с короткозамкнутым ротором состоит из двух динамических звеньев: интегрирующего звена и инерционного звена, охваченные отрицательной обратной связью [4]. Преобразователь частоты (ПЧ) представлен в структурной схеме безынерционным звеном с передаточным коэффициентом , таким же звеном представлен регулятор скорости с коэффициентом усиления .Сигнал обратной связи с выхода нелинейного звена (), на вход которого подается сигнал с выхода регулятора скорости, и сигнал с выхода датчика скорости суммируются. Полученный сигнал, проходя через усилитель, с коэффициентом усиления , подается на вход системы.

Математическое описание нелинейной системы управления ПЧ-АД можно записать в следующем виде:

(1)

(2)

где — угловая скорость двигателя; — электромагнитный момент асинхронного двигателя; статический момент двигателя; напряжение с выхода регулятора скорости, модуль жесткости механической характеристики АД; электромагнитная постоянная времени цепей статора и ротора АД; электромеханическая постоянная времени АД; передаточный коэффициент преобразователя частоты.

Уравнение замкнутого контура регулятора скорости с нелинейным звеном можно записать следующим образом:

(3)

или

(4)

здесь коэффициент регулятора скорости; коэффициент обратной связи суммирующего сигнала с выхода нелинейного звена ( и датчика скорости; коэффициент обратной связи по скорости системы ПЧ-АД.

Подставляя уравнение (4) во второе уравнение системы уравнений (1–2), после несложных преобразований, получаем следующую систему уравнений без учета задающего воздействия :

(5)

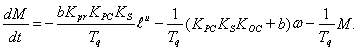(6)

Отметим, что в системе уравнений (4), в нашем случае, .

Для получения фазового портрета системы уравнений (5–6) в MATLAB преобразуем данную систему уравнений, при , к виду:

(7)

(8)

где

Численное интегрирование уравнений (7–8), с визуализацией результата решения уравнений на фазовую плоскость, осуществляется с помощью программы в системе MATLAB. Программа расчета фазовой траектории замкнутой системы ПЧ-АД системы представлена на рисунке 2.

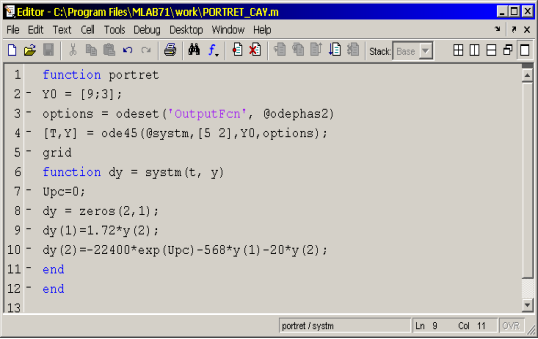
Рис. 2. Программа расчета фазового портрета системы ПЧ-АД

В программе коэффициенты системы уравнений (7–8) рассчитаны для асинхронного двигателя 4А132S6Y3 (5,5 кВT). Кроме этого, следует отметить, что в программе используется стандартная функция odephas 2MATLAB, обеспечивающая построение графика компонент решения в фазовых координатах для двумерного процесса [5].

Фазовая траектория замкнутой нелинейной системы «Преобразователь частоты — асинхронный двигатель» приведена на рисунке 3.

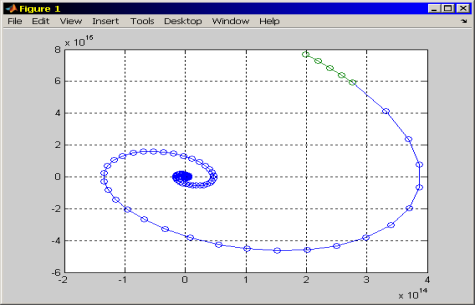
Рис. 3. Фазовая кривая замкнутой системы ПЧ-АД

Из рисунка 3 видно, что фазовая траектория системы стремится к положению равновесия (затухающий процесс). Согласно [6] система устойчива.

Выводы. Разработана математическая модель замкнутой системы ПЧ-АД.

Разработана программа расчета фазовой кривой динамики ПЧ-АД.

График фазовой кривой показывает, что замкнутая система ПЧ-АД устойчива.

Литература:

1. Фельдбаум А. А., Бутковский А. Г. Методы теории автоматического управления. — М.: Издательство «Наука», 1971.
2. Воронов А. А. Основы теории автоматического управления. Л. — М.: Издательство «Энергия», 1966.
3. Бесекерский В. А., Попов Е. П. Теория систем автоматического управления. — СПб: Издательство «Профессия», 2004.
4. Терехов И. М., Осипов О. И. Системы управления электроприводов. — М.: Издательский центр «Академия», 2008.
5. Ануфриев И. Е., Смирнов А. Б., Смирнова Е. Н. MATLAB 7. — СПб.: БХВ — Петербург, 2005.
6. Попов Е. П. Теория нелинейных систем автоматического регулирования и управления. — М.: «Наука», 1988.