В данной работе исследованы педагогические методы развития творческих способностей студентов в процессе практических занятий по электродинамике. Подчёркнута важность креативного подхода в современном образовании для развития способностей студентов. Предложена методика повышения у студентов навыков самостоятельного мышления, анализа и разработки инновационных решений на основе использования графических методов, компьютерных программ и проблемных заданий в курсах физики.
Ключевые слова: развитие креативности, электродинамика, практические занятия, графические методы, эквипотенциальные поверхности, проблемное задание, силовые линии электрического поля.
Введение
В настоящее время очень быстрое развитие науки и технологий, сопровождающееся появлением различных новых областей и направлений, приводит к обогащению научной информации, что, в свою очередь, ставит перед высшей школой актуальную задачу — воспитать не только квалифицированных специалистов, но и таких зрелых личностей, которые способны в нестандартной ситуации самостоятельно определить проблему и найти её оптимальное решение, или быстро освоить новую область знаний. В соответствии с этим требованием «социального заказа» [1] невозможно оперативно изменять учебники, учебные пособия или научные материалы для подготовки специалистов ввиду временных и экономических ограничений. Однако, как подчеркнул академик РАН Н. Бордовский, задача современного учителя состоит в том, чтобы «готовить завтрашнего специалиста на основе учебников, написанных вчера». Кроме того, как отметил известный американский педагог Джон Дьюи, в настоящее время образование следует воспринимать не как подготовку к будущему, а как образ жизни.
Для этого взаимоотношения между учителем и учеником должны строиться не по принципу «субъект — объект», а по принципу «субъект — субъект». Такой подход к образованию ставит перед учителем и учеником новые задачи, а именно: учитель должен не только давать студентам новые знания, но и мотивировать их к самостоятельной работе над собой и развитию своей личности, а также эффективно использовать новые педагогические технологии.
При формировании вышеуказанных качеств у студентов развитие их креативности является одним из основных факторов, поскольку в литературе креативность выделяется как критерий, характеризующий такие её проявления, как:
— дивергентное мышление (Дж. Гилфорд)
— интеллектуальная активность (Д. Б. Богоявлинская)
— интегративная характеристика личности (А. В. Хуторской) [1]
В учебном процессе невозможно развить креативность студента без владения фундаментальными представлениями по изучаемому предмету. [2] Кроме того, физика как наука играет большую роль в развитии креативности, поскольку она, в свою очередь, делится на разделы механики, молекулярной физики, электромагнетизма и т. д., что позволяет изучать природные процессы сразу с нескольких точек зрения. Тем не менее, физическое образование, особенно практические занятия по физике и используемые на них учебные материалы (то есть задачи), не соответствуют современным требованиям, поскольку задачи, используемые на практических занятиях, в основном являются количественными задачами с единственным решением, а лабораторная работа выполненный по инструкции не развивает самостоятельность студентов, а наоборот снижает [3]. Эти задачи и лабораторные работы по своей сути являются стандартными количественными задачами и направлены преимущественно на закрепление знаний, полученных на лекциях.
Методы и результаты
Развитие креативности обучающихся в учебном процессе могут осуществляется:
— аудиторных занятиях (лекции, практические занятия, семинары)
— самостоятельная форма обучения
При правильно выбранной образовательной технологии системная связь и преемственность аудиторного и самостоятельного обучения позволяют добиться высокой эффективности обучения, и таким образом возможно достичь развития креативности обучаемых. Кроме того, в [4] перечислены 11 основных факторов, влияющих на развитие креативности обучаемых, среди которых особенно выделяются такие, как личность преподавателя, информационное и техническое обеспечение учебного процесса, инновационные методы обучения, самостоятельное обучение и групповая работа. Исходя из особенностей образовательного процесса по физике, рассмотрим возможности достижения высокой эффективности в практических занятиях, особенно в разделах «теоретическая механика» и «электродинамика» курса теоретической физики, учитывая перечисленные выше пять отмеченных факторов.
При традиционно организованных практических занятиях можно обеспечить единство аудиторного и самостоятельного обучения с помощью использования физических задач, но при этом не достигается преемственность. Кроме того, при организации традиционных занятий по решению обыкновенных физических задач, которые используются в вузах [5, 6], инновационных технологий и групповых факторов практически незаметно, так как около 90 % задач, приведенных в сборнике, — это числовые задачи, решение которых не требует никакого анализа. Поэтому основным фактором, оказывающим наибольшее влияние на развитие креативности на практических занятиях, является личность учителя, его опыт и мастерство, поскольку опытный преподаватель может творчески подойти к задачам, приведенным в используемом в настоящее время «сборнике задач по физике», внести в них изменения и тем самым создать возможности для применения наиболее распространенной в современной педагогике технологии — информационных технологий, коллективной и самостоятельной работы. В данной статье приведена методика эффективного развития креативности студентов на практических занятиях по теоретической механике с использованием инновационных технологий при решении физических задач.
В курсах механики и теоретической механики приведена следующая задача на относительность движения:
Задача. Если колесо автомобиля радиуса R 0 = 60 см движется поступательно со скоростью 72 км/ ч, найти скорости различных точек обода колеса в различных положениях.
Данная задача относится к типовым количественным задачам и решается с использованием формулы относительных скоростей, а именно:
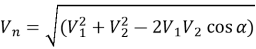
Где V1 — поступательное скорость колеса, V2 — скорость вращательного движение произвольного точки колеса.
Крайняя точка колеса участвует в двух движениях, и для обоих движений справедливо соотношение V 0 = V 1 = V 2 , в результате чего получаем выражение:
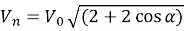
С помощью этого выражения видно, что при разных значениях угла α результирующая скорость изменяется от 0 до 2V.
Поскольку решение данной задачи не дает полного представления о физическом процессе, студент не может самостоятельно открыть для себя новые знания или закономерности, что почти не способствует развитию его креативности. Задание, данное студенту по этой теме, обеспечивает некоторую связанность аудиторного и самостоятельного обучения, но не гарантирует преемственности или командной работы, поскольку для самостоятельного изучения дается несколько подобных задач.
Как уже отмечалось, одним из основных факторов развития креативности является личность учителя. Соответственно, опытный и обладающий высоким научным потенциалом преподаватель, творчески подходя к рассмотренной задаче и используя новые педагогические технологии, достигает высокой эффективности в развитии креативности студентов. При выборе новой педагогической технологии учитель должен обратить внимание на возможности применяемой технологии при выполнении задач, направленных на достижение учебной цели. По результатам анализа, одной из наиболее перспективных образовательных технологий является организация обучения с помощью ИТ-технологий, поскольку благодаря этой технологии можно реализовать следующие задачи на основе дидактических принципов:
— получение информации в широком диапазоне о нескольких физических параметрах рассматриваемого процесса;
— построение графиков, отражающих взаимосвязь параметров, и на их основе самостоятельное открытие студентом новых закономерностей;
— одновременная организация коллективного и индивидуального обучения;
— обеспечение преемственности аудиторного и самостоятельного обучения;
— организация онлайн-контроля и консультаций и т. д.
В качестве примера, творчески переработав приведенную задачу об относительном движении, мы вносим изменения, чтобы создать условия для эффективного использования информационных технологий при её решении. Без изменения условия задачи мы ставим требование определить, как искомые физические величины зависят от различных параметров.
Известно, что любое событие или явление протекает в пространстве и во времени, поэтому студентам поручается построение графиков зависимости необходимых физических величин от пространства и времени или графиков, показывающих взаимосвязь пространства и времени. Эти задания, разумеется, комплексные и реализуются как в аудиторном, так и в самостоятельном режимах обучения.
Задача 1: Вывести зависимости от времени для координат (x,y) и скорости крайних и произвольных точек колеса.
Задача 2: Используя выражения, полученные в задаче 1, построить графики функций V x (t), V y (t), V(t), X(t), Y(t).
Задача 3: На основе выражений, полученных в задаче 1, вывести зависимости ускорения для точки обода и произвольной точки колеса.
Задача 4: Используя выражения из задачи 3, построить график зависимости модуля ускорения a(t) от времени.
Постановка задачи в таком виде формирует у студентов не только навыки аналитического решения задач и построения графиков с использованием полученных аналитических выражений на компьютере, но также приводит к пониманию того, что подобные задачи необходимо решать и численными методами. Это связано с тем, что построение графиков и выполнение простых вычислений вручную требует значительного количества времени. Кроме того, возникновение такой мысли у студентов, которые в будущем планируют заниматься научно-исследовательской деятельностью, приводит к осознанию необходимости изучения программирования.
Для решения задачи воспользуемся чертежом, приведённым на рисунке 1. В качестве начала координат выберем точку соприкосновения колеса с поверхностью. В этом случае зависимости координат x(t)x(t)x(t) и y(t)y(t)y(t) будут следующими:
Закон движения крайней точки обода колеса:
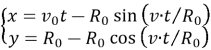
Если рассматриваемая точка расположена на расстоянии 0≤d≤R 0 от края колеса, то её закон движения имеет следующий вид:
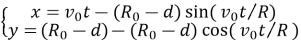
Чтобы определить скорость точки, расположенной на ободе колеса или на расстоянии d от него, берём производную по времени от выражений (1) и (2), и получаем следующие зависимости:
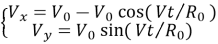
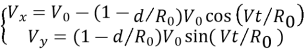
Как было отмечено выше, с помощью простых вычислений построить графики на основе этих выражений невозможно. Поэтому мы используем программу Matlab и на основе выражений (2) и (4) строим графики для значений d, лежащих в интервале 0≤d≤R 0 . При этом обязательно должно быть рассмотрено значение d=R 0 , так как в этом случае выражения (2) и (4) переходят соответственно в (1) и (3).
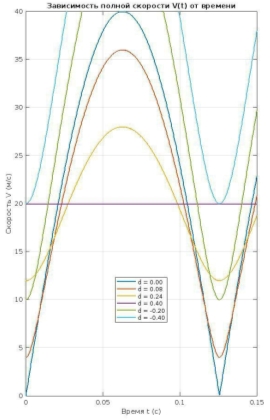
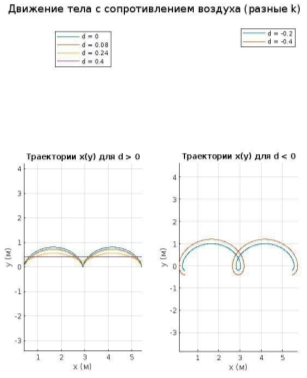
На рисунке 2 представлены графики x(t), y(t), Vx(t), Vy(t) и V(t), а на рисунке 3 — траектория f(x, y).
Следующее задание заключается в выводе выражения для ускорения произвольной точки колеса на основе ранее полученных зависимостей. Цель постановки данной задачи для студентов — сформировать у них навыки анализа и самостоятельного построения новых знаний.
У многих студентов в данной ситуации возникают ошибочные представления, например: поскольку автомобиль движется равномерно, то его ускорение равно нулю, или же, поскольку колесо вращается, ускорение можно найти по формуле
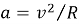
Обе вышеуказанные точки зрения не являются абсолютно неверными, однако требуют творческого подхода. В частности:
— Тангенциальное ускорение поступательного движения автомобиля и равномерного вращения его колеса равно нулю, так как автомобиль движется равномерно.
— Если рассматривать вращательное движение колеса относительно его центра, то центростремительное ускорение произвольной точки можно выразить как
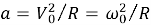
где
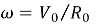
Мгновенная ось вращения — это точка касания колеса с поверхностью, а радиус вращения — расстояние от этой точки до рассматриваемой точки на колесе. Согласно схеме, приведённой на рисунке 1-б, это расстояние может быть определено следующим выражением:
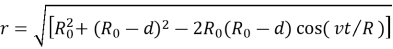
Тогда центростремительное ускорение будет определяться формулой:
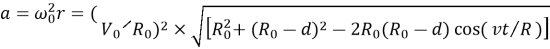
Используя данные физические параметры, строим график зависимости a(t) (рисунок 4), тем самым полностью выполняем поставленные в начальном этапе задачи.
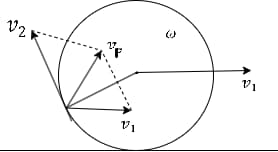
Рис. 1
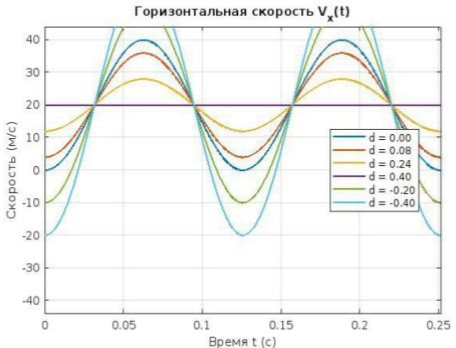
Рис. 2а
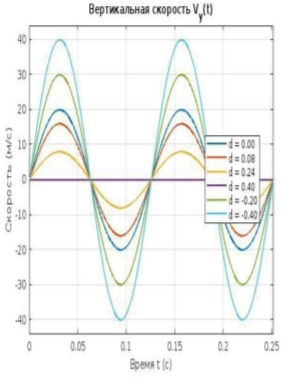
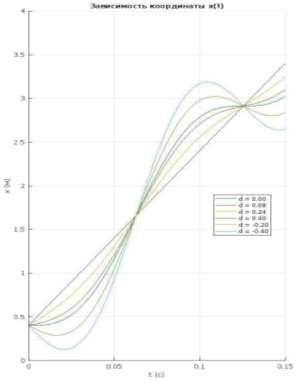
Рис. 2б
|
|
|
|
Рис. 2в |
Рис. 3а, 3б |
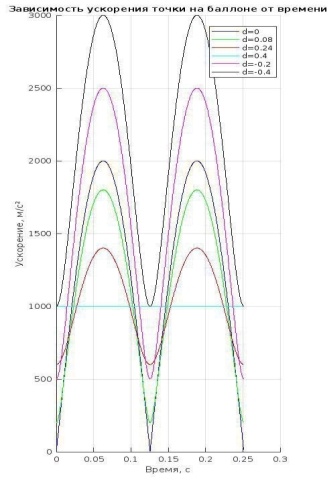
Рис. 4
Результаты и выводы
Как видно придающем этапе у студентов формируются три вида деятельности:
— анализ задачи;
— построение математической модели физического процесса;
— построение графика с использованием численного метода.
На следующем этапе студенты должны работать с графиками и на их основе выводить для себя новые закономерности.
Для этого необходимо проанализировать графики v(t), x(t), y(t), a(t) и f (x, y).
Сначала рассматриваем совместно графики траектории f(x, y), скорости v(t) и ускорения a(t) изучаемой точки. При сравнении этих графиков мы видим следующее: для точек, находящихся на расстоянии d = 0,40 м от обода колеса, графики f(x, y), v(t) и a(t) являются горизонтальными прямыми (постоянными), но их значения различаются.
Если обратить внимание на выражение (R 0 −d), при условии что R 0 =0,4 м, можно понять, что исследуемая точка совпадает с центром колеса. Для этой точки выполняются следующие закономерности:
— Траектория движения центра колеса представляет собой прямую линию.
— Скорость центра колеса постоянна и равна V 0 =20м/с, что соответствует поступательной скорости автомобиля.
— Центр колеса имеет постоянное центростремительное ускорение, значение которого
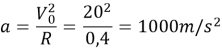
соответствует значению, вычисленному по формуле. Это означает, что центр колеса всегда совершает вращательное движение относительно мгновенной оси вращения.
Для развития креативности студентов предлагается обратная задача на основе графиков v(t), V x (t), V y (t), a(t) и f(x,y), а именно — выделить график, соответствующий случаю d<0, и ответить на следующие вопросы:
— Приведите пример движения, соответствующего случаю d<0.
— Объясните, почему на графике f(x,y) линия траектории находится ниже оси OX
— Почему V x (t) принимает только положительные значения, а V y (t)— отрицательные согласно графику?
— Объясните, почему согласно графику a(t) центростремительное ускорение всегда положительно, то есть a>0.
Кроме того, преподаватели могут задавать дополнительные вопросы, исходя из уровня подготовки студентов.
В процессе поиска ответов студенты создают для себя новые знания, физический процесс становится для них более наглядным. Кроме того, студенты осознают необходимость дополнительных графиков и взаимосвязей для получения недостающей информации. Ответы на вышеуказанные вопросы необходимо представить в письменном виде в качестве задания.
Из полученных результатов можно сделать следующие выводы. Решение физических задач с применением информационных технологий и численных методов:
— обеспечивает полное выполнение дидактических принципов — от простого к сложному, последовательности, наглядности, интегративности и преемственности;
— формирует у студентов навыки работы в команде;
— обеспечивает связность и преемственность аудиторного и самостоятельного обучения;
— формирует у студентов умение по графикам изучать физический процесс и выявлять закономерности.
Эта способность является одним из основных видов деятельности при развитии креативности. Таким образом в курсе «теоретическая механика «студентам надо предлагать задачи, при решении которых должно использоваться численное моделирование.
Литература:
- Дамбуева А. Б. Развитие креативности студентов в процессе изучения курса общей физики. Вестник ТГПУ. 2013(129) с.22–24
- Никитин. О. О. Развитие креативности как основа профессиональной подготовки студентов педагогических вузов. автореф. дис. канд.пед.наук. М., 2009.24с
- Егорова. Г. И. Развитие интеллектуальных возможностей студентов при обучении химии в техническом вузе.автореф.дис.докт.пед.наук. Тобольск 2009 45с
- Е. Е. Подгузова. Креативность личности: возможность развитие в условиях вуза./ Монография.Смоленск.2011.120 стр.
- Задачник по физике. Чертов А. Г., Воробьев А.Α.7-е изд., перераб. и доп.- М.: Физматлит. 2001.- 640 0,
- Abdumalikov. A. N " Elektrodinamika» Oliy oʻquv yurtlari uchun darslik. Toshkent.2003.320b