В статье проанализированы существующие расчётные формулы по установлению ширины устойчивого канала, проводилось сопоставление расчётных, лабораторных и натурных данных, и на базе этого получена зависимость для расчёта относительной ширины устойчивых земляных каналов в песчаных несвязанных грунтах.
Ключевые слова: канал, устойчивость, гидравлическая крупность, наносы, глубина потока, гидродинамическая устойчивость, квазиустойчивость потока.
Необходимым требованием при проектировании земляных каналов является сознание эффективной системы, которая смогла бы транспортировать заданное количество воды и наносов и не требовала бы значительных эксплуатационных затрат на русловыправительные работы на протяжении всего периода своего существования.
В настоящее время при расчёте размеров устойчивых каналов используются два основных подхода: анализ морфометрии каналов на базе теории режима и физический подход, основанный на исследовании физических процессов, протекающих в каналах с деформируемыми берегами и дном. Метод теории режима возник на рубеже XIX и XX столетий в связи со строительством оросительной системы в Индии.
Физический подход включает три основных метода расчёта каналов: метод предельной влекущей силы, разработанный в США в начале 1950-х годов, метод допустимых скоростей, созданный в СССР в 1930–1940 годах и метод определения морфометрии устойчивых каналов на базе теории гидродинамической устойчивости. Последний метод получил своё развитие сравнительно недавно (конец 60-х - начало 70-х годов), однако, несмотря на малый срок своего существования, он в ряде случаев позволил правильно описать сложные физические процессы, протекающие в каналах с подвижным ложем.
Понятие режима было сформулировано на базе натурных и лабораторных исследований, проводимых в целом ряде стран. Так, Lindley [2] следующим образом определил исходную позицию теории режима: «Размеры, ширина, глубина и клон канала для переноса определённого расхода воды и наносов всегда предопределены природой (Dynature)». Существует большое количество режимных зависимостей, подтверждаемых большим числом экспериментальных данных, к числу основных из которых можно отвести следующие:
1) [3, 4] Lacey:
Vср=
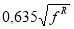
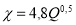
1=0,000304 f 5/6 , (3)
где: Vср –средняя скорость потока;
R –гидравлический радиус;
χ -смоченный периметр;
I –уклон канала;
ƒ –параметр заземления канала, связанный со средним диаметром донных наносов зависимостью:
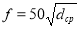
2) Lacey, Pemberton [4]
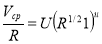
V cp =UR ( u +1)/2 1 u
где U и u –коэффициент и показатель степени соответственно, которые изменяются в зависимости от размера наносов:
U=ω½ / dс (6)
где ω –гидравлическая крупность донных наносов;
U=1, при 0,1 мм ≤ dср ≤ 0,2 мм, (7а)
U=1/2, при 0,2 мм < dср < 0,6 мм, (7б)
U=1/3, при 0,6 мм, dср < 2 мм, (7в)
U=1/4, при d > 2 мм. (7г)
3) Parker [5]:
B=4,4 Q -0,5 , (4.8)
где B=B/dср,
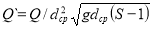
g –ускорение свободного падения;
S=ρн/ρв — относительная плотность грунта.
4) Simons, Albertson [5]:
B=k1 Q½ (8)
где k1 –размерный коэффициент (м/с), зависящий от характеристики, слагающих дно и берега канала.
5) Chitale [1]:
B=6,592 R 0,209 1– 0,097 Q 0,414 . D cp 0,115 (9)
Приведённые формулы не исчерпывают перечень существующих эмпирических зависимостей, которые почти все по своему виду представляют степенные связи между шириной, средней глубиной, уклоном дна, расходом воды и диаметром наносов и отличаются различными коэффициентами и показателями степеней.
Chitale [3] сделал обзор пригодности режимных уравнений на базе сравнения расчётных данных с измеренными характеристиками в различных системах каналов и сделал вывод, что формула (9) оказалась наиболее надёжной, чем большинство других режимных зависимостей. Обнаружено также, что коэффициент k, принимает различные значения для каналов с разными географическими условиями.
В экспериментальных условиях получены данные, позволяющие вычислить предельные тангенциальные напряжения на берегах трапецеидального канала с однородной зернистой шероховатостью. Максимальное влекущее напряжение, воздействующее на берега канала, ширина которого превышает удвоенную глубину, оценивается как 0,75 ρв g hср I.
Метод предельной влекущей силы широко используется в практике ирригационного строительства в условиях осветлённого потока [4]. Однако, как показывают последние исследования: «…проект, основанный на понятии предельного влекущего напряжения, не соответствует ирригационным каналам с подвижным дном».
Метод допустимых скоростей основан на различных расчётных формулах для определения неразмывающих и незаиляющих скоростей. В зависимости от соотношения последних производится корректировка глубины каналов с целью поддержания его равновесия (отсутствия размыва или заиления). Этот метод также предполагает отсутствие транспорта донных наносов, а для взвешенных наносов предполагается их прохождение по трассе канала транзитом. В последние годы в нашей стране и особенно за рубежом начинают использоваться результаты аналитических исследований, полученные на базе различных гидродинамических моделей, в которых плановая устойчивость каналов с подвижным ложем рассматривается в качестве одного из проявлений гидродинамической устойчивости русловых потоков. Так, в результате использования аналитической зависимости для длины плановых возмущений каналов (Lм):
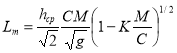
где: М –параметр Буссинеска (=22+24 м 0,5/ c );
k –параметр логарифмической функции распределения скоростей;
hср –средняя глубина потока;
С –коэффициент Шези, в преложении Lм=8В. В. С. Алтуниным предложена расчётная зависимость:
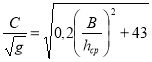
которая при заданном В/hср позволяет рассчитывать С и, наоборот, при известном С даёт возможность определить относительную ширину В/hср.
В результате решения задачи гидродинамической устойчивости канала с учётом его транспортирующей способности получено выражение для начальной длины меандров, которое в предположении условий осветлённого потока принимает вид:
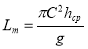
Принимая Lм=30 В в качестве характерного масштаба, при котором сохраняется условие квазиустойчивости потока, А. Е. Михиновым получена зависимость для расчёта относительной ширины устойчивых земляных каналов в песчаных несвязанных грунтах в виде:
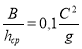
Позднее А. Е. Михиновым в результате анализа существующих режимных зависимостей с использованием метода размерностей получены зависимости для расчёта ширины и средней глубины динамически устойчивого русла, находящиеся в достаточно хорошем соответствии с эмпирическими данными.
B=7,76 d
cp
Q`
0,440
при Q`≥10
11

B=0,0023 d
cp
Q`
0,760
при 10
10
≤ Q`<10
11

B=0,30 d cp Q` 0,550 при 10 9 ≤ Q`<10 10 ;
B=88 d cp Q` 0,275 при Q`<10 9 ;
h cp =0,04 d cp Q` 0,503 при Q`>10 11 ;
h cp =10,4 d cp Q` 0,281 при 10 9 ≤ Q`≤10 11 ;
h cp =0,19 d cp Q` 0,475 при Q`<10 9 ;
где
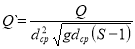
Выбор расчётной формулы для ширины канала проводится на базе сопоставления расчётных, лабораторных и натурных данных. В качестве формул проверялись зависимости (9,10,12,13). Результаты сопоставления фактических и расчётных данных представлены на рис.1. Проведённый анализ показывает, что наилучшее соответствие с фактическими данными дают зависимости (13). Это дало возможность рекомендовать её в качестве расчётной зависимости для определения ширины канала по свободной поверхности.
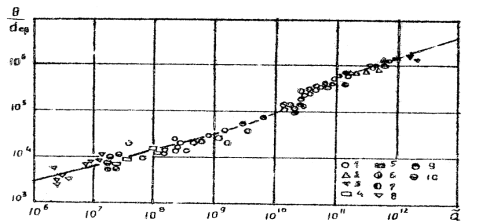
Рис.1. Сопоставления измеренных и вычисленных значений относительной ширины русла:
1—индопакистанские каналы; 2—Каракумский канал; 3—Волго-Каспийский канал; 4,8,10—лаборатоные данные; 5—Аму-Дарья; 6—Таш-Сака; 7—Кыз-Кеткен; 9—реки Белоруссии
Таким образом, полученные результаты лабораторных исследований позволяют установить устойчивые размеры канала по свободной поверхности на базе сопоставления расчётных, лабораторных и натурных данных.
Литература:
- Lane E. M. Design of stable channels. Trans. ASCE, 1955, 120–123.
- Lindley E. S. Regimb channels-Proc, Punjab end, Congress, 1919, 7, 63.
- Ибодов Р. К. «Расчет неразмывающих скоростей водного потока на дне и на откосе в грунтовых каналов». «Молодой ученый» № 47 (389), ноябрь 2021 г. (стр. 17–19), URL: https://moluch.ru/archive/389/85504/
- Ибодов Р. К. «Методы проведения экспериментальных исследований в деформируемых грунтовых открытых руслах для определения донных наносов водотоков». «Молодой ученый» № 45 (387), ноябрь 2021 г. (стр. 4–5), URL: https://moluch.ru/archive/387/85099/

