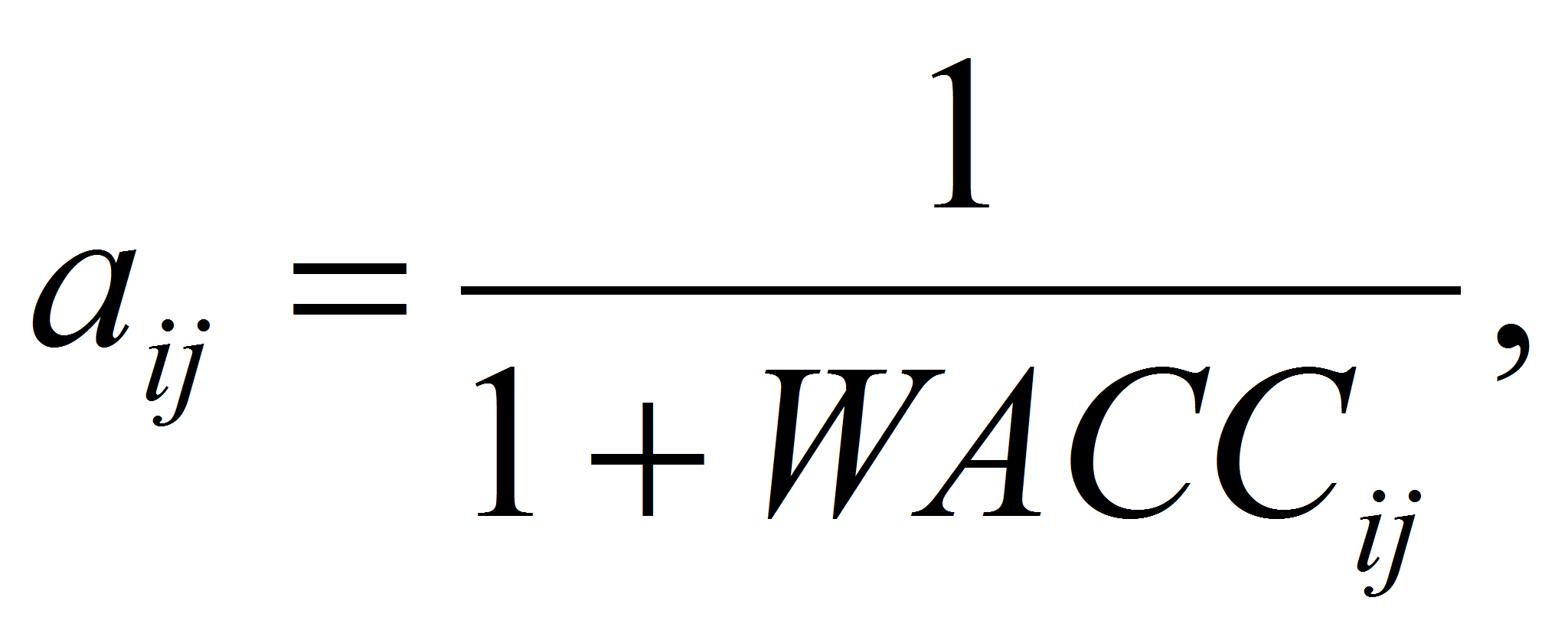Проблема поиска оптимальной структуры капитала является одной из центральных проблем современного финансового менеджмента. Особую актуальность эта проблема получает в современных условиях финансовой нестабильности, как на макроуровне, так и на уровне хозяйствующих субъектов.

При этом до сих пор не существует единого подхода к тому, какую структуру капитала считать оптимальной. Основным недостатком классических теорий структуры капитала, помимо ряда невыполнимых на практике предпосылок, на наш взгляд, можно считать тот факт, что они не позволяют в явном виде учитывать влияние конъюнктуры на структуру капиталах [7, с. 137]. В то же время такое влияние является мощным фактором неопределенности, в условиях которого финансовому менеджеру приходится принимать решение о структуре капитала.

Основной целью финансового менеджера является увеличение стоимости предприятия [5, с. 99]. Принимая во внимание тот факт, что стоимость компании находиться в обратной связи со стоимостью капитала предприятия [2, с. 157], можно сказать, что действия менеджера должны быть направлены на снижение стоимости капитала предприятия.

В качестве стоимости капитала принято использовать показатель средневзвешенной стоимости капитала WACC (weighted average cost of capital) [1, с.314]:

,

где

D_ск – доля собственного капитала,

R_ск – стоимость собственного капитала,

D_зк – доля заемного капитала,

R_зк – стоимость заемного капитала.

T – ставка налога на прибыль.

Уменьшить средневзвешенную стоимость капитала можно, либо снижая стоимости собственного и/или заемного капитала, либо меняя их соотношение.

Стоимость собственного и заемного капитала зависят от целого набора факторов (макроэкономических, политических) на которые финансовый менеджер не в силах воздействовать. Он может лишь попытаться немного сгладить влияние этих факторов. Так, например, стоимость заемного капитала определяется, в том числе, стоимостью привлечения банковских кредитов. Менеджер не может воздействовать на уровень банковских ставок в целом по банковской системе с целью его снижения. Он может только пытаться найти вариант с наиболее низкой ставкой, но, как правило, с целью обеспечения надежности кредита, выбранный вариант будет не сильно отличаться от среднего по рынку.

Однако менеджер может воздействовать на структуру капитала, меняя соотношение собственных и заемных средств. Поэтому оптимизация именно структуры капитала является одной из основных задач менеджера.

Стоимость собственного капитала представляет собой доходность, которую получают держатели акций от их владения. Составляющими такой доходности являются дивидендная доходность, а также прирост курсовой стоимости акций. На развитом рынке (например, США), дивидендная доходность является главной составляющей доходности, которую получает владелец акций: все акции, как правило, имеют длинную дивидендную историю, рост курсовой стоимости акций, как и рост всего рынка, как правило, носит умеренный характер.

На российском рынке, который находится еще на этапе становления, акции не имеют длинных дивидендных историй, а их выплата может носить нерегулярный характер. При этом рост курсовой стоимости может носить как взрывной характер, так и быть сильно отрицательно величиной.

Рост рыночной цены акции отдельной компании приводит к увеличению ее доходности. Эта доходность, являясь доходом для инвестора (владельца акции), теоретически может интерпретироваться как стоимость собственного капитала для самой компании. Например, продавая свои акции, компания привлекает некоторый объем средств, направляя его затем на финансирование своих потребностей. Затем компания может выкупить назад свои акции. С учетом того, что рыночная цена могла вырасти, переплата и составит стоимость финансирования за счет собственного капитала. Поэтому чем сильнее растет цена акции, тем выше стоимость собственного капитала компании. Как правило, рост рыночной цены акций отдельной компании происходит в рамках роста фондового рынка в целом (исключение составляют акции с отрицательным или близким к нулю коэффициентом бета, а также, зачастую, низколиквидные акции).

Если фондовый рынок находится в стадии падения, и курсовая стоимость акции также падает, то, несмотря на то, что ее владелец получает отрицательную доходность, это не означает отрицательную стоимость собственного капитала компании. Дело в том, что финансирование за счет собственного капитала происходит в рамках долгосрочного планирования, в рамках которого предполагается, что развитие компании будет приводить к росту ее стоимости, а, следовательно, и к росту ее курсовой цены. Другими словами, отрицательная стоимость по смыслу означает, что инвестор готов вкладывать средства в покупку данной акции, только если ему еще и «доплатят». Это может произойти только в том случае, если по данной бумаге не ожидается никакого дохода (актив, который в текущее время является убыточным, но имеются ожидания, что в будущем он будет приносить доход, в текущее время будет иметь положительную стоимость), что ставит под сомнение экономическую эффективность и такой компании. А значит, стоимость собственного капитала должна рассматриваться в долгосрочном аспекте, отражающем эффективность развития компании и способном нивелировать текущее негативное влияние финансового рынка.

Предложим теоретико-игровую модель выбора оптимальной структуры капитала предприятия в зависимости от «ситуации» на финансовом рынке. Сразу отметим, что данная модель будет являться моделью «игры с природой». В игре с природой, в отличие от антагонистической игры, в которой один игрок действует осознанно против другого, в качестве второго игрока выступает «природа» - некая объективная реальность, которая не действует осознанно и которая безразлична к результату игры [3, с.71].

Основными «компонентами» модели игры с природой являются игрок, природа, стратегии игрока, состояния природы, выигрыши игрока.

Положим, что в качестве игрока (ЛПР – лица принимающего решения) выступает финансовый менеджер, который принимает решения о структуре капитала компании. Стратегиями игрока являются различные варианты структуры капитала компании. Пусть игрок имеет m возможных стратегий А, которым соответствуют следующие варианты структуры капитала:

А₁: d₁=(dск/dзк)₁,

А₂: d₂=(dск/dзк)₂,

…

А_m: d_m=(dск/dзк)_m.

В качестве природы (П) примем ожидаемую среднегодовую доходность (R_m) индекса ММВБ - основного индикатора российского фондового рынка на заданном интервале (например, 3 года).

В качестве возможных состояний природы примем принадлежность ожидаемой средней годовой доходности к одному из n интервалов. Таким образом, состояние природы П_j соответствует тому, что ожидаемая средняя годовая доходность индекса ММВБ будет находиться в интервале (a_j; a_j+1).

Например, пусть природа имеет n = 5 состояний: П₁, П₂, П₃, П₄ и П₅, которым соответствуют следующие интервалы доходности индекса ММВБ:

П₁: R_m  (0; 5%],

П₂: R_m  (5%; 10%],

П₃: R_m  (10%; 20%],

П₄: R_m  (20%; 30%],

П₅: R_m  (30%; ).

Состояния природы можно определить и другим способом.

Определим в качестве выигрыша величину, обратно пропорциональную средневзвешенной стоимости капитала (WACC): 1/(1+WACC). Тогда выигрыш игрока при выборе им стратегии A_i состоянии природы П_j обозначим как a_ij:

где

WACC_ij – средневзвешенная стоимость капитала при условии соответствия структуры капитала стратегии A_i и доходности индекса ММВБ, соответствующей состоянию природы П_j.

Зависимость выигрыша от выбранной стратегии и конкретного состояния природы определяется с помощью формулы (1) и формулы САРМ:

где

R_f – безрисковая ставка доходности,

- коэффициент бетта,

R_m – доходность рынка ценных бумаг.

Матрица выигрышей (игровая матрица) А будет иметь следующий вид:

После формирования игровой матрицы можно переходить к определению оптимальной стратегии игрока. В модели игры с природой механизм поиска оптимальных стратегий состоит в следующем. В зависимости от склонности к риску игрок выбирает критерий оптимальности, в соответствии с которым он будет действовать. В соответствии с выбранным критерием для каждой стратегии вычисляется показатель эффективности стратегии. В качестве оптимальной выбирается та стратегия, которая имеет максимальный показатель эффективности. Такую стратегию называют «оптимальной по заданному критерию оптимальности». Отметим, что стратегия, оптимальная в соответствии с одним критерием оптимальности, может не быть оптимальной в соответствии с другим критерием оптимальности. Подробно о критериях оптимальности и показателях эффективности можно узнать в литературе посвященной теории игр с природой (в западной литературе теорию игр с природой обычно называют теорией статистических решений), таких как, например, [3], [4], [6].

Литература:

1. Вихори Дж. Основы финансового менеджмента. - М.: И. Д.Вильямс, 2008, с.314
2. Коупленд Т., Коллер Т., Муррин Дж. Стоимость компаний: оценка и управление. - 3-е изд., перераб. и доп. / Пер. с англ. - М.: ЗАО «Олимп-Бизнес», 2005. - 576 с, с. 157
3. Лабскер Л.Г. Теория критериев оптимальности и экономические решения: монография / Л.Г.Лабскер.-М.:КНОРУС, 2008.-744с
4. Лабскер Л.Г., Бабешко Л.О. Игровые методы в управлении экономикой и бизнесом. – М.: ДЕЛО, 2001, 464 с.
5. Осипов М.А. Определение факторов рыночной стоимости компании // Экономические науки №10(47), 2008, с. 99
6. Розен В.В. Математические модели принятия решений в экономике. – М.: Книжный дом «Университет», «Высшая школа», 2002, 287 с.
7. Снытин Р.С. Факторы оптимизации структуры капитала компании // Экономические науки №8(45), 2008, с. 137