Предложен декомпозиционный метод решения транспортной задачи с квадратичной целевой функцией. Приведены результаты численного эксперимента, иллюстрирующие возможности метода по значительному увеличению размерности решаемых задач.
1. Введение. В [1] предложен декомпозиционный (как по ограничениям, так и по целевой функции) метод решения классической транспортной задачи. В [2], [3] этот метод был перенесен на различные модификации транспортной задачи с целочисленными переменными и линейной целевой функцией. В настоящей работе рассматривается оптимизационная задача с ограничениями, совпадающими с ограничениями классической транспортной задачи и целевой функцией, квадратично зависящей от объемов перевозки. Такую задачу можно рассматривать как задачу об условном экстремуме и применить к её решению метод множителей Лагранжа. При этом с ростом размерности задачи возрастают и вычислительные трудности, не позволяющие получить решение. В работе предлагается декомпозиционный алгоритм с использованием множителей Лагранжа.
2. Постановка задачи.

При ограничениях


![]() (4)
(4)
В оптимальном решении задачи (1)-(4) переменные могут принимать как положительные, так и отрицательные значения. В данной работе, однако, будут рассматриваться задачи, в которых переменные принимают только положительные значения. Соответствующие неравенства, связывающие константы задачи, будут приведены ниже.
3. Метод решения задачи. Задачу (1)−(4) можно рассматривать как задачу на условный экстремум и использовать метод множителей Лагранжа. Этот метод приводит к необходимости решать систему из m + n линейных уравнений общего вида с m + n неизвестными. Поставив себе цель — увеличить размерность решаемых задач, поступим следующим образом. Поделим коэффициенты ![]() из (1) на 2 и найдем оптимальные решения с такой целевой функцией отдельно для ограничений первой и второй группы. Очевидно, что сумма значений целевых функций в этих оптимальных решениях будет не превосходить значения целевой функции в оптимальном решении задачи (1) − (4), а значения одних и тех же переменных не обязаны совпадать между собой. Назовем оптимальное решение, удовлетворяющее первой группе ограничений, первым псевдорешением задачи (1) − (4) удовлетворяющее второй группе ограничений — вторым псевдорешением. Решим следующую задачу с двумя ограничениями — первым ограничением из первой группы и первым ограничением из второй группы со следующей целевой функцией:
из (1) на 2 и найдем оптимальные решения с такой целевой функцией отдельно для ограничений первой и второй группы. Очевидно, что сумма значений целевых функций в этих оптимальных решениях будет не превосходить значения целевой функции в оптимальном решении задачи (1) − (4), а значения одних и тех же переменных не обязаны совпадать между собой. Назовем оптимальное решение, удовлетворяющее первой группе ограничений, первым псевдорешением задачи (1) − (4) удовлетворяющее второй группе ограничений — вторым псевдорешением. Решим следующую задачу с двумя ограничениями — первым ограничением из первой группы и первым ограничением из второй группы со следующей целевой функцией:
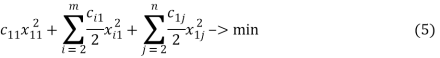


Задача (5) − (7) решается методом множителей Лагранжа. Легко видеть, что единственная стационарная точка функции Лагранжа в этой задаче является её глобальным минимумом. Заметим, что значение целевой функции в оптимальном решении задачи (5) − (7) не меньше, чем сумма значений целевых функций в оптимальных решениях задач с ограничением (6)
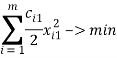
и с ограничением (7)
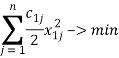
Предположим, что в оптимальном решении задачи (5)−(7) все переменные положительны. В этом случае, положив
![]()
можем записать следующие две задачи, с одним ограничением каждая:

при ограничении (6), и

при ограничении (7) обладающие следующими характеристиками. В оптимальных решениях задач (6), (8) и (7), (9) значения переменных будут совпадать, в пределах своих ограничений, со значениями переменных в оптимальном решении задачи (5) − (7), а сумма значений целевых функций в оптимальных решениях задач (6),(8) и (7),(9) будет равна значению целевой функции в оптимальном решении задачи (5)−(7). Таким образом, можно сформировать новые первое и второе псевдорешения такие, что сумма значений их целевых функций в оптимальных решениях будет больше, чем соответствующая сумма двух предыдущих псевдорешений и, как и прежде, будет не превосходить значения целевой функции любого допустимого решения задачи (1) − (4). Прорешав таким образом циклически все возможные m + n задач с двумя ограничениями, получим возрастающую ограниченную сверху последовательность сумм первых и вторых псевдорешений. При этом любой член этой последовательности не превосходит искомого минимума в задаче (1) − (4). Предел этой последовательности ввиду единственности стационарной точки и того, что она является глобальным минимумом функции Лагранжа в каждой задаче с двумя ограничениями, будет совпадать со значениями целевой функции задачи (1) − (4) в её оптимальном решении, а значения переменных в предельных одномерных задачах будут равняться значениям переменных в оптимальном решении задачи (1)−(4). Выделим класс задач, которые можно решать предложенным методом — при каких соотношениях между константами задачи (1) − (4) в оптимальных решениях задач с двумя ограничениями все переменные будут положительными. В общем случае задача с двумя ограничениями имеет вид:
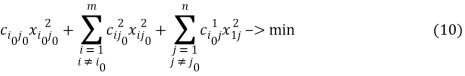


для всех
![]()
Система уравнений для нахождения ![]() имеет вид:
имеет вид:
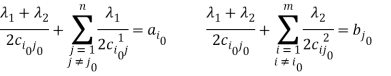
Легко видеть, что определитель системы положителен всегда. Предположим для определенности, что ![]() , тогда определитель для
, тогда определитель для ![]() также будет положительным, а для положительности определителя для
также будет положительным, а для положительности определителя для ![]() необходимо выполнение неравенства (с учетом неравенств (13)):
необходимо выполнение неравенства (с учетом неравенств (13)):
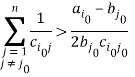
4. Результаты численного эксперимента. При вычислениях сигналом к окончанию вычислений является наличие двух обстоятельств — сгущение значений сумм целевых функций первого и двух второго псевдорешений в последовательных циклах расчетов и удовлетворение ограничениям задачи с требуемой точностью. Были решены несколько серий задач различной размерности. Стоимостные коэффициенты задавались датчиком равномерных случайных целых 4 чисел в диапазоне от 200 до 400, объемы перевозок также задавались случайным образом в диапазоне от 30 до 90 с неизбежной корректировкой для удовлетворения условиям баланса. Расчеты производились на персональном компьютере с использованием процессора с частотой 3.40GHz. В задачах с 604 пунктами производства и 594 пунктами потребления при расчетах, содержащих до 50 циклов решения задач с двумя ограничениями, на последних циклах приращение сумм целевых функций псевдорешений не превосходило долей единицы, погрешность удовлетворения ограничениями не превосходила 0.02 (при ограничении, равном 30), в остальных ограничениях погрешность не превосходила 0.000001. Время расчета максимально составляло 17 минут. В задачах, содержащих 1208 пунктов производства и 1196 пунктов потребления, для достижения аналогичных результатов потребовалось 120 циклов, максимальное время расчета составило 8 часов 20 минут.
5.Заключение. Класс задач, решаемых предложенным методом, шире, чем это указывается в достаточных условиях применимости. Возможность решения можно определить непосредственно в процессе вычислений. При необходимости можно также изменить исходные данные, если такое изменение не носит принципиальный характер. Максимальная размерность решенных задач определилась по организационным причинам, а не исходя из пределов применимости предложенного метода. В настоящее время рассматривается возможность применения данного подхода для более широкого класса задач.
Литература:
- Тизик А. П., Кузовлев Д. И., Соколов А. А., Метод последовательной модификации функционала для транспортной задачи с дополнительными пунктами производства и потребления. // Вестник ТвГУ, Серия прикладная математика, 2012, № 4, С.91–98.
- Кузовлев Д. И., Тизик А. П., Тресков Ю. П. Декомпозиционный метод для решения транспортной задачи с ограниченными пропускными способностями. // Мехатроника, автоматика, управление. 2012, № 1, С. 45–48.
- Кузовлев Д. И., Тизик А. П., Тресков Ю. П. Итеративный алгоритм для задачи о назначении. // Технические науки и практика: материалы междунар. заоч.науч. конф. (Чита, апрель 2012 г.) — Чита, Издательство Молодой учёный, 2012., С. 41–43.

