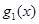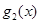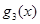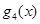Основная цель работы — показать, как решаются три задачи динамического программирования: оптимальная замена оборудования, оптимальное распределение ресурсов, минимизация затрат на строительство и эксплуатацию предприятий.
Ключевые слова: динамическое программирование, задачи оптимальной стратегии замены оборудования, оптимального распределения ресурсов, минимизации затрат на строительство и эксплуатацию предприятий.
1. Постановка задачи
Математическая наука, занимающаяся изучением экстремальных задач управления, планирования и разработкой методов их решения, называется исследованием операций.
Динамическое программирование — один из разделов исследования операций, в котором процесс принятия решения и управления может быть разбит на отдельные этапы.
Одним из основных методов динамического программирования является метод функциональных уравнений Р.Беллмана [1–4], который основывается на использовании его же принципа оптимальности. Принцип состоит в том, что, каковы бы ни были начальное состояние на любом шаге и управление, выбранное на этом шаге, последующие управления должны выбираться оптимальными относительно состояния, к которому придет система в конце данного шага. Использование данного принципа гарантирует, что управление, выбранное на любом шаге, не локально лучше, а лучше с точки зрения процесса в целом.
В задачах, решаемых методом динамического программирования, процесс управления разбивается на шаги. При распределении на несколько лет ресурсов деятельности предприятия шагом целесообразно считать временной период; при распределении средств между предприятиями — номер очередного предприятия. В других задачах разбиение на шаги вводится искусственно. Например, непрерывный управляемый процесс можно рассматривать как дискретный, условно разбив его на временные отрезки.
В данной статье решаются три задачи динамического программирования из книги [1].
2. Некоторые задачи, решаемые методами динамического программирования
2.1. Оптимальная стратегия замены оборудования.
Одной из важных экономических задач является определение оптимальной стратегии в замене старых станков, агрегатов, машин на новые. Старение оборудования включает его физический и моральный износ, в результате чего увеличиваются производственные затраты по выпуску продукции на старом оборудовании, увеличиваются затраты на его ремонт и обслуживание, снижаются производительность и ликвидная стоимость.
Наступает время, когда старое оборудование выгоднее продать, заменить новым, чем эксплуатировать ценой больших затрат; причем его можно заменить более совершенным новым оборудованием. Оптимальная стратегия замены оборудования состоит в определении оптимальных сроков замены. Критерием оптимальности при этом может служить прибыль от эксплуатации оборудования, которую следует оптимизировать, или суммарные затраты на эксплуатацию в течение рассматриваемого промежутка времени, подлежащие минимизации.
Введем обозначения: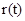 
- стоимость продукции, производимой за один год на единице оборудования возраста 
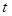лет; аналогично, 
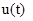и 
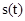— ежегодные затраты на обслуживание и остаточная стоимость оборудования возраста 
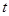лет;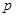 
- покупная цена оборудования.
Рассмотрим период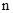 
лет, в пределах которого требуется определить оптимальный цикл замены оборудования. Обозначим через 
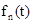максимальный доход, получаемый от оборудования возраста 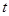лет за оставшиеся n лет цикла использования оборудования при условии оптимальной стратегии.
Возраст оборудования отсчитывается в направлении течения процесса. Так,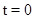 
соответствует случаю использования нового оборудования. Временные этапы процесса нумеруются в обратном направлении по отношению к ходу процесса. Так, 
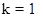относится к одному временному этапу, остающейся до завершения процесса, а 
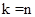- к началу процесса:
Таблица 1
|
Возраст оборудования (t) |
0 |
1 |
2 |
3 |
… |
t-1 |
t |
|
Этапы (k) |
n |
n-1 |
n-2 |
n-3 |
… |
1 |
0 |
На каждом этапе n-этапного процесса нужно принять решение о сохранении или замене оборудования. Решение должно обеспечивать получение максимальной прибыли.
Функциональные уравнения, основанные на принципе оптимальности, имеют вид:
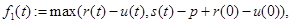(1)
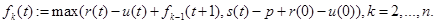(2)
Уравнение (1) описывает одноэтапный процесс, а (2) n- этапный. Оба уравнения состоят из двух частей: первая часть определяет доход, получаемый при сохранении оборудования; вторая часть — доход, получаемый при замене оборудования на новое.
В уравнении (2) функция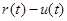 
есть разность между стоимостью произведенной продукции и эксплуатационными издержками на k –м этапе процесса. Функция 
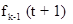характеризует суммарную прибыль от 
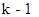оставшихся этапов для оборудования, возраст которого в начале осуществления этих этапов составляет 
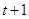лет. Вторая часть (2) характеризуется следующим образом: функция 
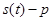представляет чистые издержки по замене оборудования, возраст которого 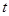лет. Функция r(0) выражает доход, получаемый от нового оборудования возраста 0 лет. Предполагается, что переход от работы на оборудовании возраста 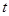лет к работе на новом оборудовании совершается мгновенно. Функция 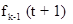представляет собой доход от оставшихся 
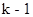этапов, до начала осуществления которых возраст оборудования составляет один год. Ясно, что 
.
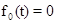Аналогичная интерпретация может быть дана уравнению для одноэтапного процесса. Здесь нет слагаемого вида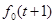 
, так как k принимает значение 1, 2,…, n.
Уравнения (1) и (2) являются рекуррентными соотношениями — функциональными уравнениями, которые позволяют определить величину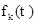 
в зависимости от .
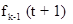Расчет начинают с использования уравнения (1). Уравнения (1) и (2) позволяют оценить варианты замены и сохранения оборудования, с тем, чтобы принять тот из них, который предполагает больший доход. Эти соотношения дают возможность не только выбрать линию поведения при решении вопроса о сохранении или замене оборудования, но и определить прибыль, получаемую при принятии каждого из этих решений. Рассмотрим пример.
Пример 1 [1]. Определить оптимальный цикл замены оборудования при следующих исходных данных: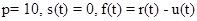 
, представленных в табл. 2.
Таблица 2
|
N |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
f(t) |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
0 |
0 |
Решение. Уравнения (1) и (2) запишем в следующем виде:
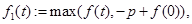(3)
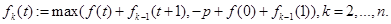(4)
Приведём программу на языке Паскаль и численный результат.
|
program zamena_oborudovaniya; const p=10; var i,j,k,n:integer; g:array[0..100] of integer; f:array[0..100,0..100] of integer; function max(a,b:integer):integer;begin if a>b then max:=a else max:=b; end; begin write('n=?'); readln(n); for j:=0 to n do begin write('g[',j,']='); readln(g[j]);end; for j:=0 to n do f[0,j]:=g[j]; for j:=0 to n do f[1,j]:=max(g[j],-p+g[0]); for i:=2 to n do for j:=0 to n-1 do begin f[i,j]:=max(g[j]+f[i-1,j+1],-p+g[0]+f[i-1,1]);end; for i:=0 to n do begin for j:=0 to n do begin write(f[i,j],' '); end; writeln;end; end. |
Результаты расчетов помещаем в таблицу (табл.3).
Таблица 3
|
10 9 8 7 6 5 4 3 2 1 0 0 0 10 9 8 7 6 5 4 3 2 1 0 0 0 19 17 15 13 11 9 9 9 9 9 9 9 0 27 24 21 18 17 17 17 17 17 17 17 17 0 34 30 26 24 24 24 24 24 24 24 24 24 0 40 35 32 31 30 30 30 30 30 30 30 30 0 45 41 39 37 36 35 35 35 35 35 35 35 0 51 48 45 43 41 41 41 41 41 41 41 41 0 58 54 51 48 48 48 48 48 48 48 48 48 0 64 60 56 55 54 54 54 54 54 54 54 54 0 70 65 63 61 60 60 60 60 60 60 60 60 0 75 72 69 67 66 65 65 65 65 65 65 65 0 82 78 75 73 72 72 72 72 72 72 72 72 0 |
По результатам вычислений и по линии, разграничивающей области решений сохранения и замены оборудования, находим оптимальный цикл замены оборудования. Для данной задачи он составляет 4 года.
2.2.Оптимальное распределение ресурсов.
Пусть имеется некоторое количество ресурсов х, которое необходимо распределить между п различными предприятиями, объектами, работами и т. д. так, чтобы получить максимальную суммарную эффективность от выбранного способа распределения.
Введем обозначения: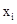
-количество ресурсов, выделенных i-му предприятию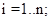 
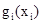- функция полезности, в данном случае это величина дохода от использования ресурса xi, полученного i-м предприятием; 
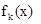-наибольший доход, который можно получить при использовании ресурсов х от первых k различных предприятий.
Сформулированную задачу можно записать в математической форме:
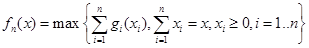. (5)
Для решения задачи необходимо получить рекуррентные — уравнения Беллмана, связывающее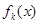 
и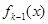 
.
Обозначим через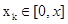 
количество ресурса, используемого k-м способом, тогда для 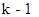способов остается величина ресурсов, равная 
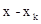. Наибольший доход, который получается при использовании ресурса 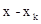от первых 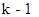способов, составит 
.
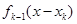Для максимизации суммарного дохода от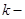 
го и первых 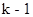способов необходимо выбрать 
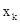таким образом, чтобы выполнялись рекуррентные — уравнения Беллмана
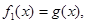
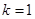, (6)
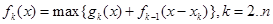. (7)
Рассмотрим конкретную задачу по распределению средств между фирмами.
Пример 2 [1]. Совет директоров рассматривает предложения для увеличения выпуска однородной продукции на четырех фирмах по наращиванию производственных мощностей.
Для расширения производства совет директоров выделяет средства в объеме 120 млн.р. с дискретностью 20 млн.р. Прирост выпуска продукции на фирмах зависит от выделенной суммы, его значения представлены фирмами и содержатся в табл. 4. Найти распределение средств между фирмами, обеспечивающее максимальный прирост выпуска продукции, причем на одну фирму можно осуществить не более одной инвестиции.
Таблица 4
|
Фирмы |
Выделяемые средства в млн. рублях |
|||||
|
20 |
40 |
60 |
80 |
100 |
120 |
|
|
Фирма№ 1 |
8 |
16 |
25 |
36 |
44 |
62 |
|
Фирма№ 2 |
10 |
20 |
28 |
40 |
48 |
62 |
|
Фирма№ 3 |
12 |
21 |
27 |
38 |
50 |
63 |
|
Фирма№ 4 |
11 |
23 |
30 |
37 |
51 |
63 |
Решение. Разобьем решение задачи на четыре этапа по количеству фирм, на которых предполагается осуществить инвестиции.
Рекуррентные соотношения для фирм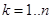 
будут иметь вид:
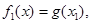
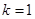, (8)
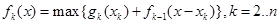. (9)
Решение будем проводить согласно рекуррентным соотношениям (8),(9).
Приведём программу на языке Паскаль и численный результат.
|
{Optimalnoe_raspredeleniye_resursov} var maxx,i,j,k,l,n,m:integer; a,b:array[0..100,0..100] of integer; function max(a,b:integer):integer; begin if a>b then max:=a else max:=b;end; begin write('n,m=');readln(n,m); for i:=1 to m do for j:=1 to n do begin write('g[',i,',',j,'] = ');readln(a[i,j]); end; for i:=0 to m do a[i,0]:=0; for j:=0 to n do a[0,j]:=0; for i:=0 to 1 do for j:=0 to n do b[i,j]:=a[i,j]; for k:=2 to m do for j:=1 to n do begin maxx:=a[k,0]+b[1,j]; for i:=1 to j do begin maxx:=max(maxx,a[k,i]+b[k-1,j-i]); end; b[k,j]:=maxx; end; for i:=1 to m do begin for j:=1 to n do write(b[i,j],' '); writeln;end; end. |
|
8 16 25 36 44 62 10 20 28 40 48 62 12 22 32 41 52 63 11 23 35 45 55 64 |
Получены условия управления от 1-го до 4-го этапа. Вернемся от 4-го к 1-му этапу. Максимальный прирост выпуска продукции в 64 млн.р. (миллион рублей.) получен на 4-м этапе как 41 + 23, т. е. 23 млн.р. соответствуют выделению 40 млн.р. четвертой фирме. Согласно 3-му этапу 41 млн. р. получено как 20 + 21, т. е. 21 млн.р. соответствует выделение 40 млн.р. третьей фирме. Согласно 2-этапу 20 млн.р. получено при выделении 40 млн. р. второй фирме. И так, инвестиции в объеме 120 млн.р. целесообразно выделить второй, третьей и четвертой фирмам по 40 млн.р. каждой, при этом прирост продукции будет максимальным и составит 64 млн.р.
2.3. Минимизация затрат на строительство и эксплуатацию предприятий.
Задача по оптимальному размещению производственных предприятий может быть сведена к задаче распределения ресурсов согласно критерию минимизации с учетом условий целочисленности, накладываемых на переменные.
Пусть задана потребность в пользующемся спросом продукте на определенной территории. Известны пункты, в которых можно построить предприятия, выпускающие данный продукт. Подсчитаны затраты на строительство и эксплуатацию таких предприятий.
Необходимо так разместить предприятия, чтобы затраты на их строительство и эксплуатацию были минимальные.
Введем обозначения: х-количество распределяемого ресурса, которое можно использовать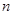 
различными способами; 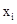- количество ресурса, используемого по i-му способу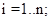 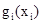-функция расходов, равная, например, величине затрат на производство при использовании ресурса 
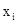по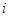 
-му способу; 
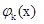- наименьшие затраты, которые нужно произвести при использовании ресурса х первыми k способами.
Минимизировать общую величину затрат при освоении ресурса x всеми способами:
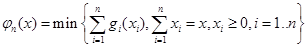(10)
Экономический смысл переменных 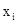состоит в нахождении количества предприятий, рекомендуемого для строительства в i-м пункте. Для удобства расчетов будем считать, что планируется строительство предприятий одинаковой мощности.
Рассмотрим конкретную задачу по размещению предприятий.
Пример 3 [1]. В трех районах города предприниматель планирует построить пять фирм одинаковой мощности по выпуску хлебобулочных изделий, пользующихся спросом.
Необходимо разместить фирм так, чтобы обеспечить минимальные суммарные затраты на их строительство и эксплуатацию. Значения функции затрат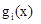 
приведены в табл. 5.
Таблица 5
|
|
1 |
2 |
3 |
4 |
5 |
|
|
11 |
18 |
35 |
51 |
76 |
|
|
10 |
19 |
34 |
53 |
75 |
|
|
9 |
20 |
36 |
54 |
74 |
Здесь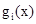 
-функция расходов, определяющая величину затрат на строительство и эксплуатацию в зависимости от количества размещаемых предприятий в i-м районе;
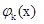-наименьшая величина затрат в млн.р., которые нужно произвести при строительстве и эксплуатации предприятий в первых k районах.
Решение. Решим задачу с использованием рекуррентных соотношений по районам 
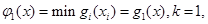(11)
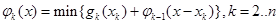. (12)
Приведём программу на языке Паскаль и численный результат.
|
{Minimizatsiya rasxodov} var minn,i,j,k,l,n,m:integer;a,b:array[0..100,0..100] of integer; function min(a,b:integer):integer;begin if a<b then min:=a else min:=b; end; begin write('n,m=');readln(n,m); for i:=1 to m do for j:=1 to n do begin write('g[',i,',',j,'] = ');readln(a[i,j]);end; for i:=0 to m do a[i,0]:=0; for j:=0 to n do a[0,j]:=0; for i:=0 to 1 do for j:=0 to n do b[i,j]:=a[i,j]; for k:=2 to m do for j:=1 to n do begin minn:=a[k,0]+b[1,j]; for i:=1 to j do begin minn:=min(minn,a[k,i]+b[k-1,j-i]); end; b[k,j]:=minn; end; for i:=1 to m do begin for j:=1 to n do write(b[i,j],' ');writeln; end; end. |
|
11 18 35 51 76 10 18 28 37 52 9 18 27 37 46 |
Минимально возможные затраты при х = 5 составляют 46 млн. р. Определены затраты на строительство предприятий от 1-го до 3-го этапа. Вернемся 3-го к 1-му этапу. Минимальные затраты в 46 млн. р. на 3-м этапе получены как 9 + 37, т. е. 9 млн. р. соответствуют строительству одного предприятия в третьем районе. Согласно 2-му этапу 37 млн. р. получены как 19 + 18, т. е. 19 млн. р. соответствуют строительству двух предприятий во втором районе. Согласно 1-му этапу 18 млн. р. соответствуют строительству двух предприятий в первом районе.
Итак, оптимальная стратегия состоит в строительстве одного предприятия в третьем районе, по два предприятия во втором и первом районах, при этом минимальная стоимость строительства и эксплуатации составит 46 ден. ед.
Литература:
1. Красс М. С., Чупрынов Б. П. Основы математики и ее приложения в экономическом образовании: Учеб. — 2-е изд., испр. — М.: Дело, 2001. — 688 с.
2. Таха Х. А. Введение в исследование операций, — М.: «Вильямс», 2005. — 912 с..
3. Охорзин В. А. Прикладная математика в системе MathCAD. -СПб, Лань.2008.-352 с.
4. Писарук, Н. Н. Исследование операций. — Минск: БГУ, 2014. —289 c.
5. Имомов А., Эргашев Б. С. Организация решения задач исследования операций в MATHCAD,. Молодой учёный, 8 (88), 2015 г.-с.5–9.
