В настоящей работе изучается обобщенная модель Фридрихса. На примере рассматриваемого оператора, с помощью леммы Морса получено разложение соответствующего определителя Фредгольма.
Ключевые слова: обобщенная модель Фридрихса, пространство Фока, определитель Фредгольма, лемма Морса.
Поведения определителя Фредгольма для двухчастичного дискретного оператора Шредингера изучены в работах [1–3], a для семейства модели Фридрихса с одномерным возмущением, которые ассоциированы с системой двух частиц на решетке изучен в работах [4,5]. Как известно, что некоторые актуальные задачи, в частности, задачи квантовой механики, статистической механики и гидродинамики сводятся к исследованию спектральных свойств обобщенной модели Фридрихса [6,7]. Поэтому изучение поведения определителя Фредгольма для обобщенной модели Фридрихса играет важную роль в современной математической физике. При этом лемма Морса о локальном приведении гладкой вещественнозначной функции к каноническому виду в окрестности невырожденной критической точки является основным инструментом. Это лемма красива сама по себе и важна в приложениях. Лемма Морса является один из основных результатов теории Морса, названной по имени разработчика теории и установившего данный результат в 1925 году американским математиком Х. К. М. Морса (1892–1977).
Ради удобства для читателей сначала сформулируем лемму Морса [8].
Лемма Морса. Пусть 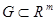 - открытое множество, функция
- открытое множество, функция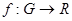 принадлежит классу
принадлежит классу 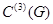 и
и 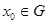 невырожденная критическая точка этой функции. Тогда существует диффеоморфизм
невырожденная критическая точка этой функции. Тогда существует диффеоморфизм 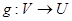 отображающее некоторое окрестность
отображающее некоторое окрестность 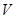 точки
точки 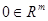 в окрестность
в окрестность 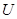 точки
точки 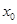 такое, что
такое, что
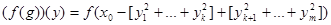
для любых 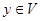 .
.
Пусть 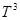 - трехмерный тор,
- трехмерный тор, 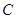 - одномерное комплексное пространство,
- одномерное комплексное пространство, 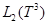 - гильбертово пространство квадратично-интегрируемых (комплекснозначных) функций, определенных на
- гильбертово пространство квадратично-интегрируемых (комплекснозначных) функций, определенных на 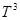 . Обозначим через
. Обозначим через 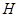 прямую сумму пространств
прямую сумму пространств 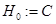 и
и 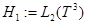 , т. е.
, т. е. 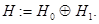
Рассмотрим обобщенную модель Фридрихса 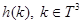 , действующую в гильбертовом пространстве
, действующую в гильбертовом пространстве 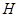 по формуле
по формуле
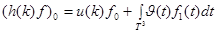 ;
; 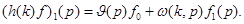
Здесь 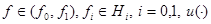 и
и 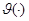 -вещественнозначные непрерывные функции на
-вещественнозначные непрерывные функции на 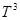 , а функция
, а функция 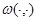 -вещественнозначная непрерывная симметрическая функция на
-вещественнозначная непрерывная симметрическая функция на 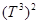 . Очевидно, что оператор
. Очевидно, что оператор 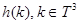 ограничен и самосопряжён в
ограничен и самосопряжён в 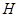
Отметим, что обобщенная модель Фридрихса 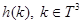 обладает основными спектральными свойствами двухчастичного дискретного оператора Шредингера (см. например [9]). По этой причине гильбертово пространство
обладает основными спектральными свойствами двухчастичного дискретного оператора Шредингера (см. например [9]). По этой причине гильбертово пространство 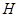 называется двухчастичным обрезанным подпространством Фоковского пространства, а обобщенная модель Фридрихса
называется двухчастичным обрезанным подпространством Фоковского пространства, а обобщенная модель Фридрихса 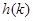 называется гамильтонианом системы с не более чем двумя частицами на решетке.
называется гамильтонианом системы с не более чем двумя частицами на решетке.
Для точной формулировки нужного нам результата, приведем несколько условий:
Условие 1. a) Функция 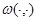 является четной в
является четной в 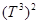 по совокупности переменных
по совокупности переменных 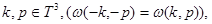 имеет единственный невырожденный минимум в точке
имеет единственный невырожденный минимум в точке 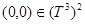 и все частные производные четвертого порядка функции
и все частные производные четвертого порядка функции 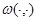 непрерывны в
непрерывны в 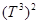 ;
;
б) Существуют положительно определенная матрица 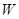 , числа
, числа 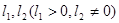 такие, что
такие, что
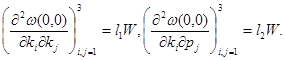
Из условие 1 вытекает, что 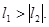
Условие 2. Функции 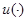 и
и 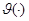 четны, а также функция
четны, а также функция 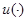 имеет единственный минимум в точке
имеет единственный минимум в точке 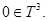
Замечание 1. Условия 1–2 выполняются в случае, когда
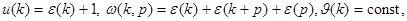
где функция  определена по формуле
определена по формуле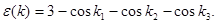
При каждом фиксированном 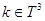 определим регулярную в
определим регулярную в 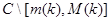 функцию (определитель Фредгольма, ассоциированный с оператором
функцию (определитель Фредгольма, ассоциированный с оператором 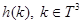 )
)
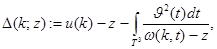
где числа 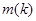 и
и 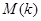 определяются следующим образом:
определяются следующим образом:
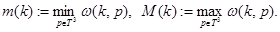
В силу условие 1 функция 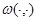 имеет единственный невырожденный минимум в точке
имеет единственный невырожденный минимум в точке 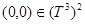
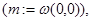 а функция
а функция 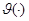 является аналитической на
является аналитической на 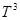 по предположению, поэтому существует конечный интеграл
по предположению, поэтому существует конечный интеграл
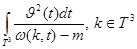 .
.
Из теоремы о предельном переходе под знаком интеграла Лебега следует, что
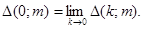
Положим
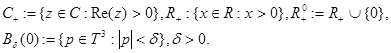
Теперь сформулируем результат о разложении определителя Фредгольма.
Теорема 1. Пусть выполнены условия 1–2. Существует число 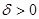 , такое, что для любых
, такое, что для любых 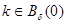 и
и 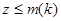 имеет место представление
имеет место представление
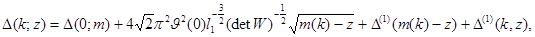
где 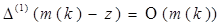 при
при 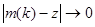 и
и 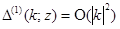 при
при 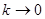 равномерно по
равномерно по 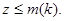
Доказательство. Пусть функция 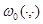 определена в
определена в 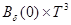 как
как
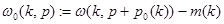 ,
,
где 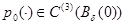 и для любого
и для любого 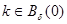 точка
точка 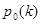 является точкой невырожденного минимума.
является точкой невырожденного минимума.
При каждом 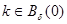 определим аналитическую функцию
определим аналитическую функцию 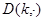 в
в 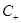 по формуле
по формуле
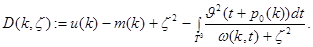
Так как 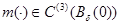 в силу определение функции
в силу определение функции 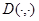 условие 1,2 получим, что функция
условие 1,2 получим, что функция 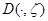 принадлежит классу
принадлежит классу 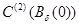 для любых
для любых 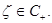
Пользуясь разложением
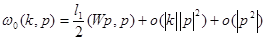
при 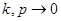 получим, что существует число
получим, что существует число 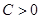 такое, что при всех
такое, что при всех 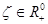 и
и 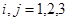 имеет место неравенства
имеет место неравенства
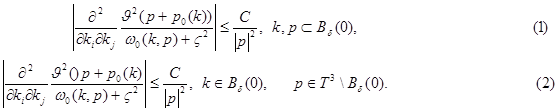
В силу теоремы Лебега о предельном переходе имеем
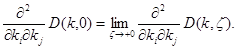
Применяя лемму Адамара получим, что
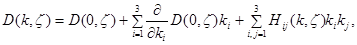
где при каждом 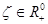 функция
функция 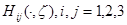 является непрерывной в
является непрерывной в 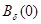 и
и
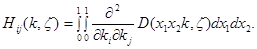
В силу неравенств (1) и (2) имеем
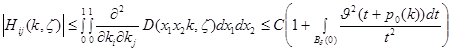
для любых 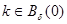 равномерно по
равномерно по 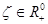 .
.
При каждом 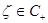 функция
функция 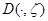 является четной в
является четной в 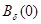 и поэтому
и поэтому
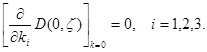
Таким образом, при каждом 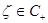 функция
функция 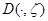 принадлежит классу
принадлежит классу 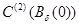 и имеет место разложение
и имеет место разложение 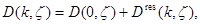 где
где 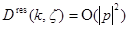 при
при 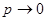 равномерно по
равномерно по 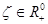 .
.
Теперь докажем, что существует правая производная от 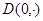 в точке
в точке 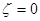 и имеет место оценка
и имеет место оценка
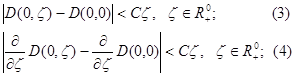
для некоторого 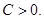
Действительно, функцию 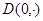 можно представит в виде
можно представит в виде 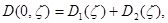
где
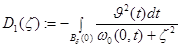 ,
, 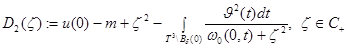 .
.
Так как функция 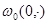 является непрерывной в компактном множестве
является непрерывной в компактном множестве 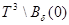
и имеет единственный минимум в точке 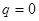 существует число
существует число 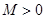 такое, что
такое, что 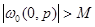 для любых
для любых 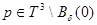 . Тогда из
. Тогда из 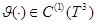 вытекает, что
вытекает, что
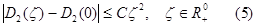
для некоторого 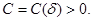
Рассмотрим следующий разность
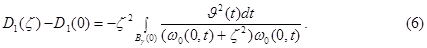
Функция 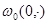 имеет единственный невырожденный минимум в точке
имеет единственный невырожденный минимум в точке 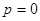 .
.
Следовательно, в силу леммы Морса существует взаимно-однозначное отображение
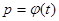 из
из 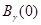 в некоторое окрестность
в некоторое окрестность 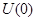 точки
точки 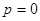 такое, что
такое, что
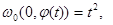 (7)
(7)
где 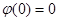 и для Якобиана
и для Якобиана 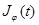 отображении
отображении 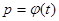 имеет место равенство
имеет место равенство 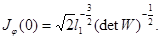 В интеграле (6) делая замену переменных
В интеграле (6) делая замену переменных 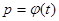 и пользуясь равенством (7) имеем
и пользуясь равенством (7) имеем
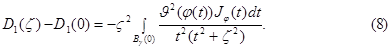
В интеграле (8) переходя в сферическую систему координат 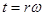 запишем ее в виде
запишем ее в виде
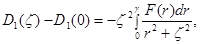
где 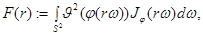
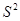 - единичная сфера в
- единичная сфера в 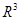 , a
, a 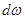 элемент единичной сферы. Учитывая факты
элемент единичной сферы. Учитывая факты 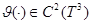 и
и 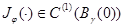 имеем
имеем
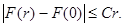 (9)
(9)
Теперь согласно оценки (9) получим
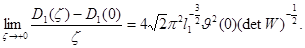
Следовательно, существует правая производная функции 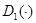 в точке
в точке 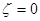 и
и
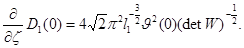
Таким образом,
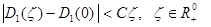 (10)
(10)
для некоторого 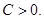
Тогда из неравенств (5) и (10) следует, что существует правая производная функции 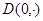 в точке
в точке 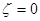 и
и 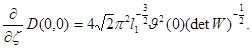 Сопоставляя неравенства (5) и (10) получим (3). Аналогично доказывается оценка (4). Теперь утверждение теоремы вытекает из равенства
Сопоставляя неравенства (5) и (10) получим (3). Аналогично доказывается оценка (4). Теперь утверждение теоремы вытекает из равенства 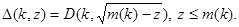 Теорема доказана.
Теорема доказана.
Литература:
1. S. Albeverio, S. N. Lakaev, K. A. Makarov, Z. I. Muminov. The threshold effects for the two-particle Hamiltonians in lattice // Comm. Math. Phys. — 2006, — V. 262, P. 91–115.
2. S. Albeverio, S. N. Lakaev, Z. I. Muminov. Schroedinger operators on lattices. The Efimov effect and discrete spectrum asymptotics // Ann. Henri Poincare, — 2005, — V. 5, — P. 743–772.
3. Абдуллаев Ж. И., Лакаев С. Н., Асимптотика дискретного спектра разностного трехчастичного оператора Шредингера на решетке // Теор. и мат. физ., — 2003, — Т. 136, — № 2, С. 231–245.
4. S. Albeverio, S. N. Lakaev, Z. I. Muminov. The threshold effects for a family of Friedrichs models under rank one perturbations // J. Math. Anal. Appl. — 2007, — V. 330, — P. 1152–1168.
5. Т. Х. Расулов Т. Х. Асимптотика дискретного спектра одного модельного оператора, ассоциированного с системой трех частиц на решетке // Теор. и матем. физ. — 2010, — Т. 163, — № 1, С. 34–44.
6. Л. Д. Фаддеев. О модели Фридрихса в теории возмущений непрерывного спектра // Труды Мат. Инс-та АН СССР, -1964, — Т. 73, — С. 292–313.
7. Р. А. Минлос, Я. Г. Синай. Исследование спектров стохастических операторов, возникающих в решетчатых моделях газа // Теор. и матем. физ. -1979, — Т. 2, — № 2, — С. 230–243.
8. В. А. Зорич. Математический анализ. Часть I. Изд-во ФАЗИС, Москва, 1997.
9. S. Albeverio, S. N. Lakaev, T. H. Rasulov. The Efimov Effect for a Model Operator Associated with the Hamiltonian of a non Conserved Number of Particles // Methods Func. Anal. Topol. — 2007, -V. 13, — no. 1, — P. 1–16.

