Метод дифференциальной прогонки развивается для решения широкого класса краевых задач дифференциальных уравнений четвертого порядка с переменными коэффициентами. В ряде прикладных задач показывается эффективность предлагаемого метода как способа алгоритм решения подобных задач.
Ключевые слова:дифференциальная прогонка, задача Коши, метод Канторович — Власова, изгиб балки переменного сечения, цилиндрической оболочки переменной толщины, прямоугольной пластинки переменной жесткости.
Приближенные решения уравнений математической физики, дифференциальных и интегральных чаще всего строятся на основе так называемых прямых методов, позволяющих свести построение приближенного решения данной задачи к решению систем линейных (если данная задача также линейная) алгебраических уравнений. Как хорошо известно, прямые методы прекрасно зарекомендовали себя на практике и получили широкое распространение; чаще других используются различные варианты метода сеток. Однако наряду со многими достоинствами, прямые методы имеют и один важный недостаток: чтобы получить более высокую точность приближения, приходится повышать порядок алгебраической системы, что часто приводит к неустойчивости вычислительного процесса. Для метода сеток увеличение порядка алгебраической системы ведёт к увеличению числа ее обусловленностей, что влечет за собой накопление ошибок при решении системы и, как следствие понижение точности. Добавим к этому, что машинное решение алгебраических систем высокого порядка наталкивается еще на специфические трудности, связанные с ограниченностью памяти ЭВМ.
Высказанные здесь соображения делают, по-видимому, целесообразной попытку использовать для приближенного решения задач математической физики методы, не требующие применения систем алгебраических уравнений высоких порядков. В связи с этим в данной статье мы постараемся показать, как можно заменить линейные краевые задачи для обыкновенных дифференциальных уравнений четвертого порядка задачами Коши, для решения которых существуют устойчивые численные методы. При этом будем пользоваться специальными преобразованиями искомых решений, сводящих краевые задачи к задачам Коши. Подобные преобразования для обыкновенных дифференциальных уравнений второго порядка имеются в работах [1,2].
Будем рассматривать краевые задачи только для линейных обыкновенных дифференциальных уравнений четвертого порядка с переменными коэффициентами. Распространение предлагаемого метода в сочетании с методом Канторовича — Власова или методом прямых на уравнения с частными производными в ряде случаев очевидно.
Рассмотрим дифференциальное уравнение
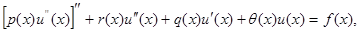(1)
где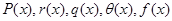 
-известные функции при различных граничных условиях.
I. Пусть граничных условиях для уравнения (1) будут следующие:
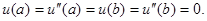(2)
Введя обозначения
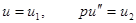(3)
Напишем уравнение (1) в виде
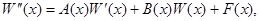(4)
Где
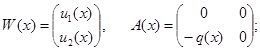
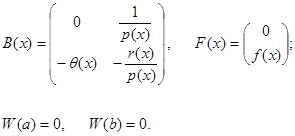(5)
Ищем решение уравнение (4)
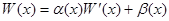(6)
С начальным условием
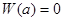(7)
Где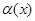 
- 2-мерная матрица, 
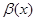- 2-мерный вектор. Тогда для нахождения 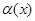и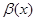 получим уравнения
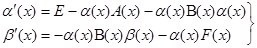(8)
С начальными условиями
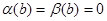(9)
Таким образом, краевая задача (1)-(2) свелась к задачам Коши (6)-(7), (8)-(9).
Применяем изложенных методов к некоторым задачам теории упругости.
1. Изгиб балки переменного сечения, лежащей на упругом основании. Основное разрешаемое уравнение-
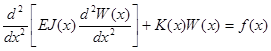(10)
где Е — модуль упругости,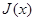 
- момент инерции сечения, 
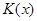- переменный коэффициент.
Если, балка свободно опертая, то граничные условия точно совпадают с граничными условиями (2).
Следовательно, полагая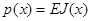 
, 
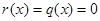и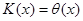 
, из решений уравнения (1) найдем решения уравнения (3).
Если один край балки жестко защемлен, а другой — свободный, то граничные условия для уравнения (10) будут такие:
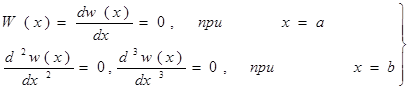(11)
2. Изгиб цилиндрической оболочки переменной толщины под действием симметричной относительно оси нагрузки.
Основное разрешаемое уравнение имеет вид [3]
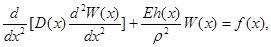(12)
где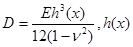 
- переменная толщина, 
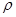- радиус оболочки, 
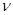- коэффициент Пуассона.
Уравнение (12) полностью идентично уравнению (16), поэтому решения о соответствующими граничными условиями получаем аналогичным образом.
3. Изгиб прямоугольной пластинки переменной жесткости.
Рассмотрим задачу об изгибе пластинки, когда жесткость является функцией от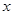 
. Тогда основной разрежаемое уравнение данной задачи запишется так [3]:
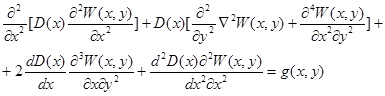(13)
Граничные условия для пластинок следующие:
a) жестко защемленной
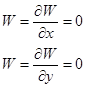при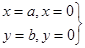 
; (14)
b) свободно опертой
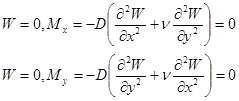при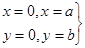 
; (15)
c) свободной
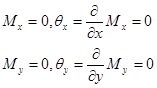при 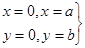; (16)
Решение уравнения (13) ищем в виде
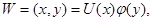(17)
где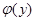 
- известные координатные функции, удовлетворяющие граничным условиям пластинки при y=0, y=b. Подставляя предполагаемое решение (17) и (13) и выполняя процедуры метода Канторовича — Власова, придем к уравнению
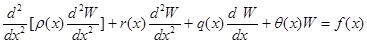, (18)
где
, 
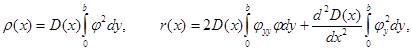
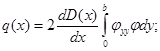
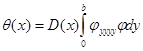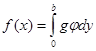
Таким образом, уравнения (10), (12) и (18) соответствующими граничными условиями с успехом могут быть решены предлагаемым методом.
Литература:
1. С. С. Ирискулов, М. Олимов, К. Исманова, А. Имомов. Численные методы и алгоритмы. Учебное пособие., Наманган, Изд-во «Наманган», 2013, 278с.
2. Олимов М., Каримов П., Исмоилов Ш.. К решению краевых задач пространственных стержней при переменных упруго-пластических нагружений с учетом разгрузки // Научно- технический журнал ФерПИ, Фергана — 2014. — № 3 — с. 113–116.
3. Тимошенко С. П., Войновский-Кригер С. Пластинки и оболочки. М., «Наука», 1966.
