В настоящее время появилась возможность решения математических задач без составления компьютерных программ на языках программирования. Причиной этого является разработка специальных математических программ — математических систем. В научных исследованиях и в вузах на занятиях больше всего применяются следующие математические системы: MathCAD, MATLAB, Maple, Mathematika [1–3]. С применением математических систем учебный процесс становится интереснее, студенты понимают содержание занятия быстрее, глубже, а для укрепления понятий и решения задач остаётся больше времени.
В последнее время задачи вычислительной математики [1,2] часто решают в математической системе MATHCAD. При этом используют разные подходы: одни применяют внутренний язык MATHCAD, другие пытаются реализовать численный математический алгоритм [3–7].
В статье алгоритмы методов коллокации, Галёркина, наименьших квадратов, разностных схем приближённого решения линейного обыкновенного дифференциального уравнения (ОДУ) с краевыми условиями (КУ) организованы в математической системе MATHCAD.
1. Краевая задача для ОДУ. Сведения о приближённых методах.
Для линейного ОДУ краевая задача ставится следующим образом:
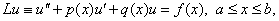 (ОДУ), (1)
(ОДУ), (1)
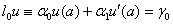 ,
, 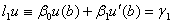 , (КУ). (2)
, (КУ). (2)
Необходимо найти функцию 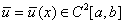 , удовлетворяющую ОДУ и краевым условиям (КУ) (2).
, удовлетворяющую ОДУ и краевым условиям (КУ) (2).
В проекционных методах [1,2] приближённое решение 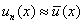 отыскивается в виде конечной суммы с неопределёнными коэффициентами:
отыскивается в виде конечной суммы с неопределёнными коэффициентами:
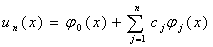 ,
, 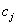 -?. (3)
-?. (3)
Здесь начальная функция 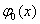 и базисные функции
и базисные функции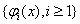 определяются требованиями конкретных методов:
определяются требованиями конкретных методов:
1) 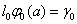 ,
,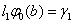 ,
, 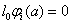 ,
,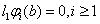 .
.
2) 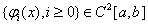 .
.
3) система 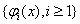 линейно независима и полна на отрезке
линейно независима и полна на отрезке 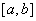 .
.
При таком выборе имеет место сходимость 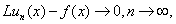 а в случае ограниченности
а в случае ограниченности 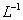 имеет место сходимость
имеет место сходимость 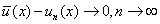 [1].
[1].
Для определения неизвестных коэффициентов введем функцию невязки
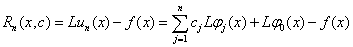 . (4)
. (4)
В методе коллокации коэффициенты 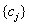 определяются из условий совпадения
определяются из условий совпадения 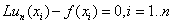 , что эквивалентно линейной системе уравнений:
, что эквивалентно линейной системе уравнений:
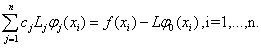 (5)
(5)
В методах Галеркина коэффициенты 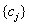 определяются из условия ортогональности
определяются из условия ортогональности 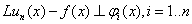 , что эквивалентно линейной системе уравнений:
, что эквивалентно линейной системе уравнений:
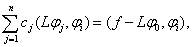
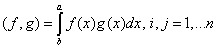 . (6)
. (6)
В основе методе Ритца лежит идея минимизации квадратичного функционала:
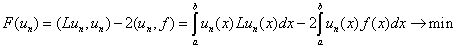 , (7)
, (7)
которая опять приводит к системе (6). В методе Ритца предполагается симметричность и положительная определённость оператора 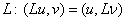 ,
, 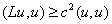 ,
, 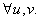
В методе наименьших квадратов коэффициенты 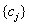 определяются из условия ортогональности
определяются из условия ортогональности 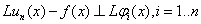 , что эквивалентно линейной системе уравнений:
, что эквивалентно линейной системе уравнений:
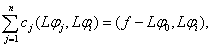
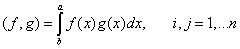 . (8)
. (8)
2. Выбор базисных фунций [2,4]. Для каждого типа краевых условий предлагаем два варианта базисных функций.
Краевые условия 1-го типа: 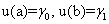 ,
,
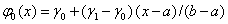 ,
, 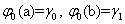 , (10)
, (10)
а)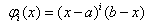 ; б)
; б)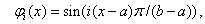
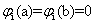 ,
, 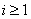 . (11)
. (11)
Краевые условия 2-го типа: 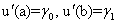 ,
,
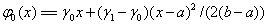 ,
, 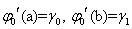 . (12)
. (12)
а)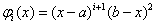 ; б)
; б)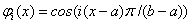 ,
,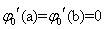
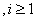 . (13)
. (13)
Краевые условия 3-го типа: 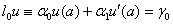 ,
,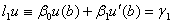 .
.
Полагая, 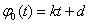 имеем
имеем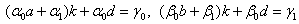 . Отсюда, согласно правилу Крамера находим
. Отсюда, согласно правилу Крамера находим 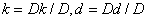 , где
, где
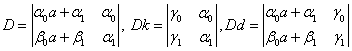 .
.
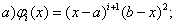
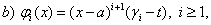
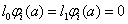 . (14)
. (14)
3. Организация решения задачи в MathCAD
В качестве примера рассмотрим ОДУ [2] с параметрами
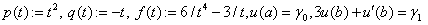 ,
,
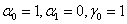 ,
,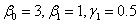 .
.
В качестве базисных функций принимаем 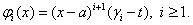
Базисную функцию 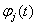 в MATHCAD удобно обозначить так
в MATHCAD удобно обозначить так 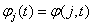 . Ещё введём обозначения
. Ещё введём обозначения 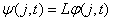 ,
,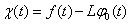 .
.
Команды в MATHCAD записываются без всякого предопределителя, и отличаются от математических формул лишь следующей разницей: комбинация знаков двоеточие и равно, т. е. (:=), означает определение, знак равно (=) или стрелка (→) означает вывод вычисленного значения. Кроме того, после ввода знака «открывается поле для ввода текста-замечания и по окончании ввода — замечания и нажатия клавиши Enter остаётся только текст-замечание. Мы в местах, где должен быть текст-замечание записываем знак «и, после него, вводим текст-замечание. Это облегчает понимание алгоритма решения.
Записываем в MATHCAD следующие команды:
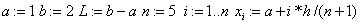
«Определимначальную функцию 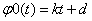 из условий
из условий 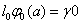 ,
,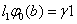 .
.
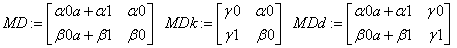
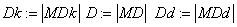
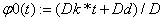
«Определимбазисные функции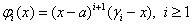 ,
, 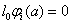 ,
,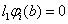 .
.
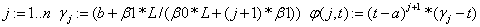 «базисные функции
«базисные функции
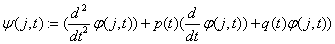 «вспомогательная функция
«вспомогательная функция
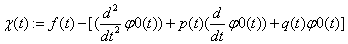 «вспомогательная функция
«вспомогательная функция
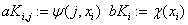 «элементы метода коллокации
«элементы метода коллокации
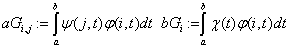 «элементы метода Галёркина
«элементы метода Галёркина
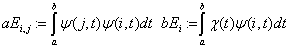 «элементы метода МНК
«элементы метода МНК
«Для контроля вычислений можно вывести на экран матрицы и правые части, полагая
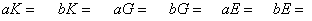 «вывод матрицу, правую часть
«вывод матрицу, правую часть
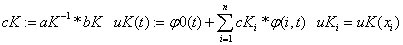 «метода коллокации
«метода коллокации
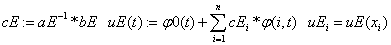 «метод наименьших квадратов
«метод наименьших квадратов
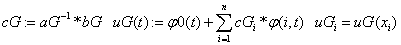 «метод Галёркина
«метод Галёркина
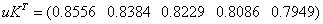 «вычисление значений
«вычисление значений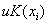
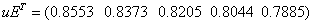 «вычисление значений
«вычисление значений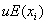
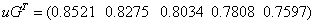 «вычисление значений
«вычисление значений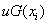
Для сравнения найденных значений сведём их в таблицу:
|
Методы/узлы |
1,0333 |
1,0667 |
1,1 |
1,1333 |
1,1667 |
|
Коллокации |
0,8556 |
0,8384 |
0,8229 |
0,8086 |
0,7949 |
|
МНК |
0,8553 |
0,8373 |
0,8205 |
0,8044 |
0,7885 |
|
Галёркина |
0,8521 |
0,8275 |
0,8034 |
0,7808 |
0,7597 |
Используя базисные функции 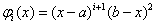 , найдем почти такие же значения.
, найдем почти такие же значения.
4. Организация вычислений решения краевой задачи для линейного ОДУ с помощью разностных схем.
Для ОДУ, разностная схема имеет следующий вид:
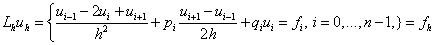 , (15)
, (15)
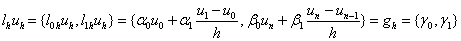 . (16)
. (16)
Преобразуем эту систему линейных уравнений в систему:
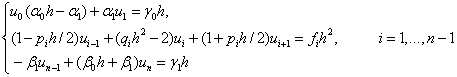
Вводя следующие обозначения
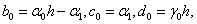
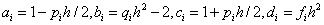 ,
,
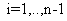 ,
, 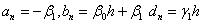
приходим к стандартной трехдиогнальной системе линейных уравнений:
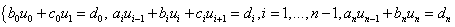 .
.
Трехдиогнальную систему линейных уравнений можно решать методом прогонки. В методе прогонки решения системы линейных уравнений разыскивается в виде 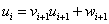 , где коэффициенты прогонки
, где коэффициенты прогонки 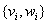 и неизвестные
и неизвестные 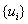 определяются формулами:
определяются формулами:
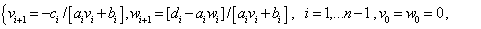 (17)
(17)
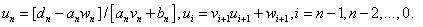 (18)
(18)
Формулы (17) определяют прогоночные коэффициенты 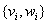 , а формулы (18) определяют неизвестные
, а формулы (18) определяют неизвестные 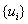 .
.
Решение задачи в MathCAD.
В качестве примера рассмотрим ДУ с параметрами
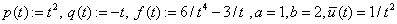 .
.
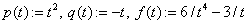 «
«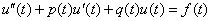
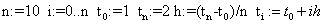 «отрезок, параметры
«отрезок, параметры
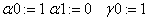 «коэффициенты КУ
«коэффициенты КУ
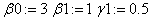 «коэффициенты КУ
«коэффициенты КУ
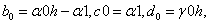 «коэффициенты 0-уравнения СЛАУ
«коэффициенты 0-уравнения СЛАУ
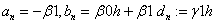 «коэффициенты n-уравнения СЛАУ
«коэффициенты n-уравнения СЛАУ
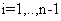 ,
, 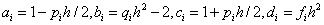 «коэффициенты. i-го уравнения
«коэффициенты. i-го уравнения
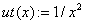
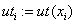 «точное решение и его значения
«точное решение и его значения
«коэффициенты 0-уравнения в MathCAD
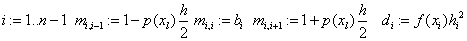 «коэф.i-уравнения.
«коэф.i-уравнения.
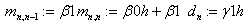 «коэффициенты n-уравнения в MathCAD.
«коэффициенты n-уравнения в MathCAD.
Для контроля выведем на экран MathCAD элементы системы уравнений:
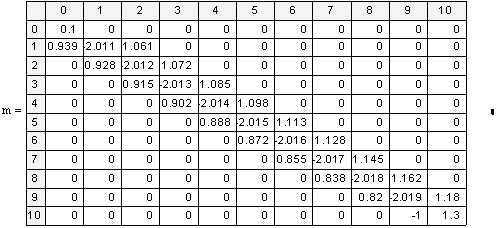

«Выведем таблицу значений приближённого и точного решений на экран MathCAD:
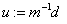
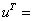
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
0,8276 |
0,6963 |
0,5941 |
0,5131 |
0,4478 |
0,3944 |
0,3502 |
0,3132 |
0,282 |
0,2554 |
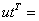
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
0,8264 |
0,6944 |
0,5917 |
0,5102 |
0,4444 |
0,3906 |
0,346 |
0,3086 |
0,277 |
0,25 |
Как видно из таблиц значений приближённое и точное решение совпадают с точностью 0.01.
Литература:
1. Марчук Г. И. Методы вычислительной математики. М.: Наука, 1981.
2. Вержбицкий В. М. Численные методы. М.:ООО, ”ОНИКС-21 век”, 2005.-400 с.
3. Имомов А. Организация численных методов в MathCAD. Молодой учёный, № 6(65), май 1, 2014 г.-с. 15–19.
4. Ирискулов С. С., Исманова К. Д., Олимов М., Имомов А. Численные методы и алгоритмы. MathCAD. Учебное пособие.. Наманган, Изд-во «Наманган»,2013.-278с.
5. Поршнев С. В., Беленкова И. В. Численные методы на базе MathCAD. СПб, 2005.-464 с.
6. Ракитин В. И. Руководство по ВМ и приложения MathCAD.М.:ФМ, 2005.-264 с.
7. Охорзин В. А. Прикладная математика в системе MathCAD. СПб, Лань,2008–352 с.







