Работу складского комплекса можно сравнить со сложной системой, где объемы грузов и интенсивность поступающего транспорта постоянно меняются. Из-за нестабильности рыночного спроса невозможно точно предсказать, сколько товаров будет проходить через склад в среднесрочной и долгосрочной перспективе. Это приводит к тому, что нагрузка на склад носит неравномерный, пульсирующий характер.

Из-за естественных экономических циклов (например, сезонов, дней недели или времени суток) нагрузка на склад постоянно меняется, то резко возрастая, то падая. Эта неравномерность приводит к двум крайностям:

– В моменты наплыва заказов система перегружается, вызывая «логистический шторм» — то есть, пробки из транспортных средств под погрузку и разгрузку.

– В периоды затишья, наоборот, возникает «ресурсный парадокс» — дорогостоящие мощности и работники вынуждены простаивать, что делает работу склада неэффективной.

Чтобы минимизировать влияние «ресурсного парадокса», необходима четкая система планирования ресурсов, основанная на прогнозах будущей загрузки склада. Центральной задачей управления становится поиск оптимального баланса ключевых параметров:

– достаточное количество погрузочно-разгрузочных мест (доков) для обработки грузопотоков;

– оптимальная численность сотрудников, исключающая как простои, так и перегрузки;

– размер парка погрузчиков, соответствующий операционным потребностям;

– объемы резервных площадей для хранения, позволяющие справляться с пиковыми нагрузками [1].

При построении такой модели принципиальными требованиями являются ее универсальность, адаптивность и практическая применимость для широкого класса складских систем. Этим критериям в полной мере отвечает аппарат теории массового обслуживания (ТМО). Данный математический инструмент позволяет абстрагировать складской комплекс в виде системы обслуживания, где входящий поток заявок (транспортные средства) обслуживается каналами (доками, бригадами) с определенной интенсивностью, что позволяет количественно оценить вероятности образования очередей и простоев и найти точку баланса между стоимостью содержания ресурсов и потерями от их недостатка. [2]

Складской комплекс (СК), как и любая другая система массового обслуживания, может быть формализована через набор фундаментальных компонентов:

1. Обслуживающие аппараты (каналы)- совокупность ресурсов, обрабатывающих материальный поток. К ним относятся рампы (доки) с погрузочно-разгрузочной техникой, зоны комплектации заказов, системы сортировки, а также складской персонал (кладовщики, операторы).
2. Входящий поток — заявки, требующие обслуживания. В контексте СК это не только прибывающие грузовые автомобили, но и внутренние заявки на отбор товара со стеллажей для формирования заказов.
3. Накопители (очередь)- образования, возникающие в периоды, когда интенсивность входящего потока превышает пропускную способность каналов. Это могут быть физические очереди автотранспорта на подъездных путях или виртуальные очереди заказов в WMS (складской управляющей системе), ожидающие обработки.
4. Обработка заявки- результат завершения обслуживания — отгруженные машины с товаром, укомплектованные и переданные в доставку заказы [3].

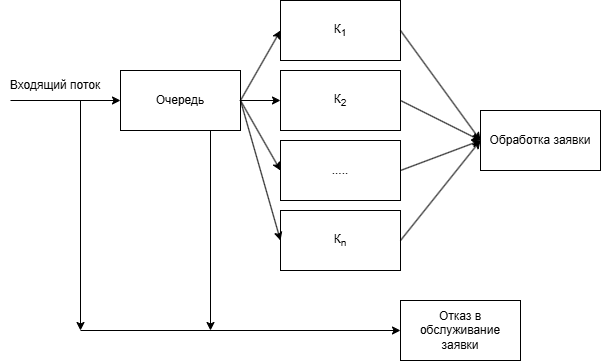
Рис. 1. Общая схема системы массового обслуживания

В рамках данного исследования предлагается математическая модель СМО, репрезентирующая работу распределительного складского центра. Модель нацелена на поиск оптимального соотношения между количеством обслуживающих каналов и потерями, вызванными очередями и простоями, для минимизации совокупных логистических издержек.

Характер потока грузовиков не является постоянным. В масштабах недели или месяца поток сильно неравномерен из-за сезонности, нерегулярности поставок и логистических циклов. Однако на коротких промежутках (например, в течение стандартного рабочего дня с 10:00 до 18:00) его можно считать условно стабильным и описывать моделью Пуассона со средней интенсивностью λ (лямбда).

В целом, интенсивность прибытия транспорта зависит от времени суток и дня недели λ(t), что отражает циклы деловой активности: резкое падение ночью и пиковые нагрузки в определенные дни.

Поскольку прибытие автотранспортных средств на складской комплекс является результатом большого числа независимых решений (отправителей, перевозчиков), не скоординированных между собой, можно считать, что входящий поток заявок обладает свойством отсутствия последействия. Это означает, что момент поступления очередной заявки не зависит от предыстории процесса.

На практике заявки могут поступать в систему не только поодиночке, но и группами (пакетами). Ярким примером является прибытие сборного грузовика, который доставляет множество заказов для разных получателей одновременно, или координация поставок от крупного клиента несколькими машинами в одном временном окне. В этом случае, помимо моделирования потока пакетов, необходимо учитывать случайную величину X — размер пакета (количество заказов или условных единиц груза в одной прибывшей единице транспорта). Это существенно усложняет модель, переводя её в разряд систем массового обслуживания (СМО) с групповым входящим потоком (M/M/n/m).

Если же сделать допущение, что заявки (автомобили) поступают поодиночке, независимо друг от друга и с постоянной средней интенсивностью λ в течение рассматриваемого интервала, то такой поток может быть описан простейшим пуассоновским потоком. Для такого потока вероятность поступления ровно k заявок (транспортных средств) за время t определяется распределением Пуассона [2]:

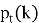
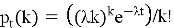
Рассматривается многоканальная система массового обслуживания (СМО) с ожиданием и ограниченной длиной очереди, моделирующая работу складского комплекса на примере автотранспорта. На вход системы, содержащей n обслуживающих каналов (разгрузочно-погрузочных рамп/доков), поступает простейший пуассоновский поток заявок (автотранспортных средств) с интенсивностью λ.

Дисциплина обслуживания функционирует по следующему принципу:

1. Немедленное обслуживание- поступившая заявка (автомобиль), заставшая хотя бы один свободный канал, немедленно занимает его и начинает обслуживаться (процесс разгрузки/погрузки).
2. Ожидание в очереди- если в момент поступления все n каналов заняты, заявка становится в очередь. Длина очереди физически ограничена числом m, которое определяется пропускной способностью маневровой зоны склада.
3. Отказ в обслуживании- заявка, заставшая в системе уже n каналов и m заявок в очереди (т. е. общее число заявок в системе равно n + m), получает отказ и покидает систему необслуженной. Для склада это означает потерю клиента или вынужденный перенос поставки [4].

Время обслуживания одной заявки одним каналом является случайной величиной, подчиняющейся экспоненциальному закону распределения. Это допущение коррелирует с реальной практикой, где длительность операции зависит от множества случайных факторов (тип груза, человеческий фактор). Среднее время обслуживания одной заявки составляет , где μ — интенсивность обслуживания (среднее число заявок, обслуженных одним каналом в единицу времени).

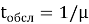
Данная модель относится к классу M/M/n/m (марковская система с пуассоновским входным потоком, экспоненциальным временем обслуживания, n каналами и ограничением на длину очереди m) и позволяет вычислить ключевые показатели эффективности склада, такие как:

– Вероятность отказа (доля потерянного товаропотока);

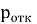
– Относительная пропускная способность Q (доля обслуженного потока);

– Средняя длина очереди (оценка загруженности подъездной территории);

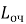
– Среднее время ожидания в очереди (показатель соблюдения сроков).

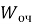
Для формального анализа рассматриваемой M/M/n/m-системы складского комплекса необходимо описать все возможные состояния системы. Можно выделить 4 принципиально разных макросостояния:

– Все обслуживающие каналы (доки) свободны;

– Часть обслуживающих каналов занята, часть свободна;

– Все обслуживающие каналы заняты, очередь отсутствует;

– Все обслуживающие каналы заняты, в очереди находятся заявки.

Для детального математического описания вводится набор дискретных состояний , где индекс k (от 0 до n+m) обозначает общее количество заявок, находящихся в системе в данный момент (т. е. либо обслуживаемых, либо ожидающих в очереди).

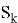
В контексте работы складского комплекса состояния СМО интерпретируются следующим образом:

— все n доков свободны, очередь пуста.

– один док занят обслуживанием автомобиля, остальные n-1 доков свободны.

...

– заняты n-1 доков, один док свободен.

– все n доков заняты, очередь отсутствует.

– все доки заняты, в очереди находится одна машина.

...

– все n доков заняты и все m мест в очереди заполнены (система полностью насыщена).

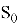
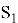
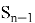
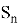
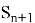
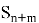
Переход системы из одного состояния в другое является марковским процессом и обусловлен двумя типами событий:

1. Поступление новой заявки с интенсивностью λ переводит систему из состояния в состояние (до тех пор, пока k < n+m).
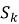
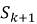
2. Завершение обслуживания заявки одним из каналов с интенсивностью переводит систему из состояния состояние . При этом, если в системе находится k заявок и k ≤ n (все заявки на обслуживании), то интенсивность завершения обслуживания равна k * μ (работают k каналов). Если k > n, то интенсивность завершения обслуживания постоянна и равна n * μ (работают все n каналов).

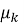
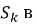
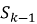
Изучение динамики таких систем являются дифференциальные уравнения, описывающие вероятности нахождения системы в каждом из состояний в любой момент времени, известные как уравнения Колмогорова [2]. Для установившегося режима работы производные приравниваются к нулю, что позволяет получить систему линейных алгебраических уравнений для нахождения финальных вероятностей состояний , которые являются основой для расчёта всех ключевых показателей эффективности склада.

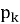
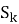
Поскольку число прибывающих в складской комплекс (СК) автотранспортных средств (АТС) представляет собой дискретную случайную величину (счётное множество значений), принимающую целые неотрицательные значения с вероятностью, задаваемой формулой Пуассона [2], данная величина распределена по закону Пуассона с параметром λ. Важнейшим свойством этого распределения является равенство математического ожидания и дисперсии параметру λ:

M(X) = D(X) = λ.

Это означает, что среднее количество прибывающих АТС и разброс вокруг этого среднего за фиксированный промежуток времени численно равны интенсивности входного потока. Процесс обработки АТС в СК является многоэтапным и может быть представлен в виде последовательности или сети СМО, где каждый этап требует отдельного моделирования. Блок-схема технологического процесса обслуживания АТС может включать несколько сценариев, существенно влияющих на общее время пребывания в системе (См. рис.2).

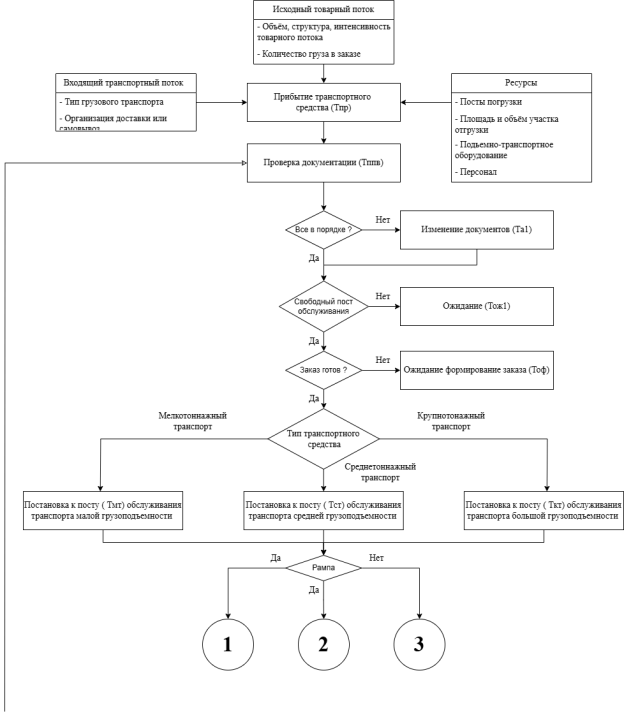
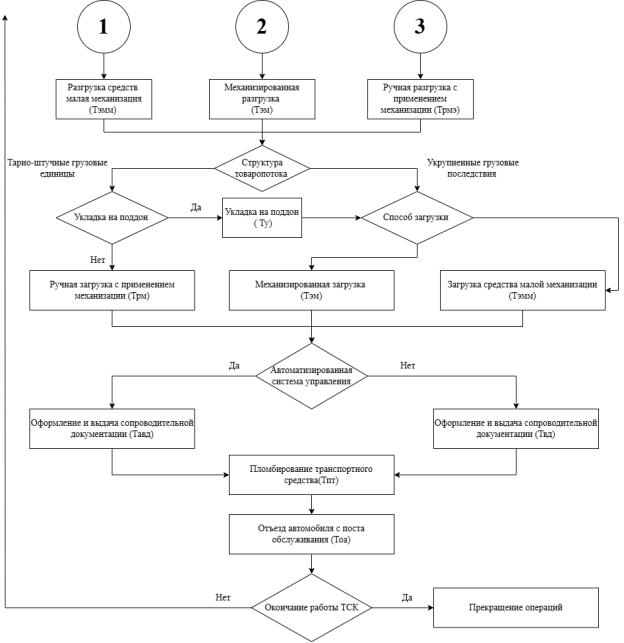
Рис. 2. Блок-схема технологического процесса складского комплекса при обслуживании автотранспорта прибывшего на пост обслуживания

Например:

Этап 1 (Прибытие транспортного средства): Прибывшее АТС проходит процедуру идентификации и оформления документов. Данный этап может быть смоделирован как многоканальная СМО с ограниченной очередью. Если документы не оформлены заранее, АТС либо проходит эту процедуру (переходя в состояние обслуживания), либо, при невозможности оформления, покидает комплекс (получает отказ).

Этап 2 (Зона ожидания): После оформления АТС направляется в зону ожидания. Наличие свободного дока (канала обслуживания) проверяется. При его отсутствии АТС занимает место в очереди, что представляет собой многоканальную СМО с ожиданием.

Этап 3 (постановка к посту обслуживания): При освобождении дока АТС занимает его для проведения погрузочно-разгрузочных работ (РПР). Данный этап также является многоканальной СМО, где каналы — это доки.

Таким образом, общая модель складского комплекса представляет собой сложную сеть СМО, где выходной поток одного этапа является входным для последующего. Для адекватного моделирования необходимо учитывать не только параметры каждого узла сети ( , , , ), но и дисциплину маршрутизации потоков между ними. [5].

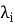
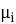
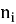
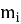
Перечислим возможные сценарии процесса обслуживания АТС в СК:

Сценарий 1. Идеализированная модель с мгновенным обслуживанием.

Рассматривается частный, идеализированный случай функционирования складского комплекса, при котором выполняются следующие допущения:

Все необходимые административные процедуры (оформление документов) завершены заранее.

На момент прибытия автотранспортного средства (АТС) в системе имеется как минимум один свободный обслуживающий канал (док), очередь перед комплексом отсутствует.

В данных условиях на вход многоканальной системы массового обслуживания, содержащей n каналов (доков), поступает простейший поток заявок (АТС) с интенсивностью λ. Поскольку количество свободных каналов всегда не менее единицы, а очередь невозможна, любая поступившая заявка немедленно принимается на обслуживание. Следовательно, система функционирует в режиме с отказами, где отказ возникает только в гипотетическом состоянии полной занятости всех каналов, однако при выполнении условия k < n (где k — число заявок в системе) это состояние недостижимо в установившемся режиме.

Граф состояний такой системы представляет собой линейную цепь марковского процесса и представлен на рисунке.

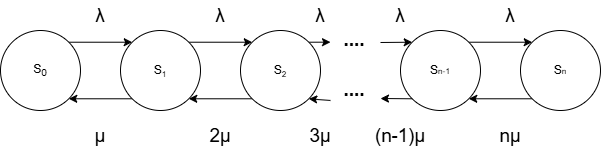
Рис. 3. Граф состояний многоканальной СМО.

Возможны следующие состояния СМО , где индекс k (0 ≤ k ≤ n) обозначает количество одновременно занятых доков:

— все n доков свободны.

— один док занят обслуживанием АТС, остальные (n-1) доков свободны.

— два дока заняты, остальные (n-2) свободны.

...

— все n доков заняты. Поступление новой заявки в этом состоянии в рамках данной модели приводит к отказу.

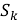
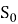
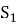
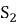
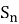
Интенсивности переходов между состояниями определяются следующим образом:

Переход из состояния в состояние происходит с интенсивностью λ (поступление новой заявки).

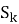
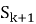
Переход из состояния в состояние происходит с интенсивностью k * μ, где μ — интенсивность обслуживания одним каналом. Это отражает тот факт, что завершить обслуживание может любой из k занятых каналов.

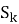
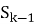
Данная модель, известная как M/M/m/n (система с отказами Эрланга), позволяет рассчитать важнейшую характеристику для данного сценария — вероятность немедленного начала обслуживания, которая эквивалентна вероятности того, что в системе находится менее n заявок.

В рамках рассмотренной идеализированной модели с отказами, финальные (предельные) вероятности состояний системы определяются через параметр ρ = λ / μ (приведённая интенсивность потока) по следующим формулам:

, для k = 1, 2,..., n

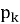
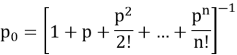
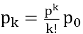
Определив вероятности всех состояний СМО, можно рассчитать её ключевые характеристики. Абсолютная пропускная способность системы (A), определяющая среднее число заявок, обслуживаемых в единицу времени, дополняет вероятность отказа до интенсивности входного потока и рассчитывается как:

A = λ * (1 - )

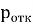
Где — вероятность отказа, возникающая в состоянии, когда все n каналов заняты.

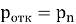
Заключение

Таким образом, в зависимости от комбинации организационных и технологических факторов, можно выделить следующие обобщённые сценарии обслуживания АТС в складском комплексе:

Сценарий 1. Оптимальная загрузка. Все документы оформлены заранее, и на момент прибытия АТС имеется достаточное количество свободных доков. Модель: M/M/m/n (система с отказами).

Сценарий 2. Ожидание с предварительным оформлением. Документы оформлены, но все доки заняты. АТС занимает место в очереди ограниченной длины. Модель: M/M/n/m (система с ожиданием).

Сценарий 3. Ожидание с оформлением в реальном времени. Документы не оформлены, но доки свободны. АТС последовательно проходит этапы оформления (одна СМО) и затем обслуживания на доке (другая СМО). Модель: Последовательная сеть СМО.

Сценарий 4. Комплексное ожидание. Документы не оформлены, и все доки заняты. АТС сталкивается с очередью как на этапе оформления, так и на этапе погрузки/разгрузки. Модель: Сеть СМО со взаимозависимыми очередями.

Сценарий 5. Обслуживание с предварительной подготовкой. Документы оформлены, и доки свободны, но требуют предварительной подготовки (например, разгрузки прибывшего контейнера). Модель: M/M/n/m с дополнительной случайной задержкой перед началом обслуживания.

Литература:

1. Вентцель Е. С. Исследование операций: задачи, принципы, методология. — М.: КноРус, 2018. — 208 с.
2. Попов, А. М. Глава 7. Элементы теории массового обслуживания / А. М. Попов, В. Н. Сотников // Теория вероятностей: учебник для вузов / А. М. Попов, В. Н. Сотников. — Москва: Юрайт, 2023. — С. 210–245. — ISBN 978–5–9916–1234–5.
3. Ларичев О. И., Абрамов А. Н. Применение теории массового обслуживания для повышения эффективности работы логистического терминала // Транспорт: наука, техника, управление. — 2021. — № 8. — С. 45–50.
4. Смирнов, В. В. Повышение эффективности взаимодействия терминально-складских комплексов и грузового транспорта: магистерская диссертация: 23.04.02 / Смирнов Василий Васильевич; место защиты: Институт транспортной техники и систем управления. — Москва: РУТ (МИИТ), 2024. — 134 с.
5. Козловская Э. А., Лебедев А. В. Оптимизация работы зоны разгрузки распределительного центра на основе теории массового обслуживания // Вестник ИрГТУ. — 2017. — № 5 (124). — С. 154–161.