Введение
Законы Ньютона в форме задачи двух тел справедливы только при предположении центрального гравитационного поля. Для геостационарных спутников это предположение нарушается вследствие: — неравномерного распределения массы Земли; — гравитационного воздействия Луны и Солнца; — давления солнечного излучения.
Следствием является отклонение орбиты от Кеплеровой и необходимость регулярного поддержания орбиты.
Геостационарная орбита и параметры движения
Период обращения геостационарного спутника равен периоду вращения Земли:
T = 2π / ωₑ ≈ 86164 с,
где ωₑ — угловая скорость вращения Земли.
Радиус геостационарной орбиты определяется выражением:
r_GEO = (μ / ωₑ²)^(1/3) ≈ 42164 км,
где μ = GMₑ — гравитационный параметр Земли.
При малых эксцентриситетах используются компоненты вектора эксцентриситета:
eₓ = e · cos(Ω + ω)
eᵧ = e · sin(Ω + ω)
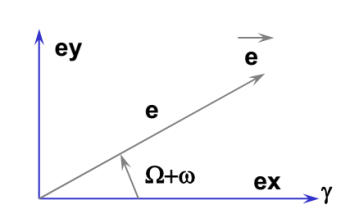
Рис. 1. Вектор эксцентриситета в плоскости (eₓ, eᵧ).
Возмущения гравитационного поля Земли
Нецентральность гравитационного потенциала
Гравитационный потенциал Земли с учётом сплюснутой представляется разложением:
U(r,φ) = μ/r · [1 − Σ Jₙ (Rₑ / r)ⁿ Pₙ(sinφ)],
где Jₙ — коэффициенты гармоник, Pₙ — полиномы Лежандра.
Наибольшее влияние на геостационарную орбиту оказывает коэффициент J₂.
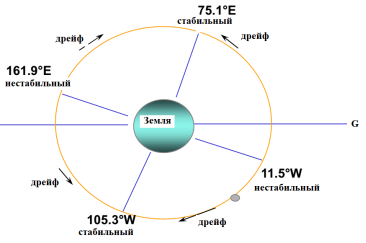
Рис. 2. Экваториальное выпячивание Земли и возникающая возмущающая сила
Дрейф долготы
Для спутника вблизи устойчивой долготы λₛ справедливо уравнение:
d²λ / dt² = C = const.
Интегрирование даёт:
λ(t) = (C/2)·t² + λ̇₀·t + λ₀.
Таким образом, долгота изменяется по параболическому закону.
Лунно‑солнечные гравитационные возмущения
Возмущающее ускорение от третьего тела (Луны или Солнца) записывается как:
a₃ = μ₃ · [(r₃ − r)/|r₃ − r|³ − r₃/|r₃|³].
Воздействие на наклонение
Секулярный дрейф наклонения имеет вид:
di/dt ≈ 0.75° — 0.95° в год.
Без коррекции наклонение за несколько лет достигает недопустимых значений.
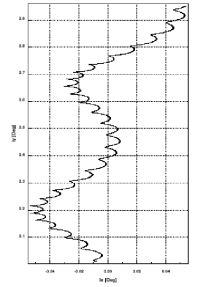
Рис. 3. Свободная эволюция вектора наклонения (iₓ, iᵧ)
Периодические эффекты
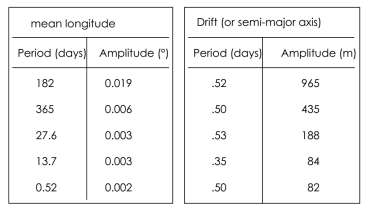
Лунно‑солнечные возмущения вызывают также периодические изменения эксцентриситета и средней долготы с периодами от 14 суток до 1 года.
Таблица 1
Периодические лунно‑солнечные возмущения долготы и полуоси
Давление солнечного излучения
Среднее давление солнечного излучения на расстоянии орбиты Земли:
P₀ = 4.56 × 10⁻⁶ Н/м².
Сила, действующая на элемент поверхности dA:
dF = P · cosθ · dA.
С учётом отражения и поглощения результирующая сила записывается как:
F = −P [(1 − Cₛ) S + (2 Cₛ cosθ + 2/3 C_d) N] cosθ · dA.
Эволюция вектора эксцентриситета
Интегрирование уравнений движения приводит к выражениям:
eₓ = A₀ + eₙ cos lₛ,
eᵧ = B₀ + eₙ sin lₛ,
где lₛ — эклиптическая долгота Солнца.
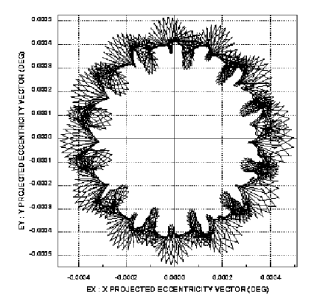
Рис. 4. Годовая эволюция вектора эксцентриситета под действием солнечного давления
Поддержание геостационарной орбиты
Поддержание орбиты включает коррекции: — восток–запад (долгота); — север–юг (наклонение).
Годовые затраты характеристической скорости:
ΔV_NS ≈ 45–50 м/с в год.
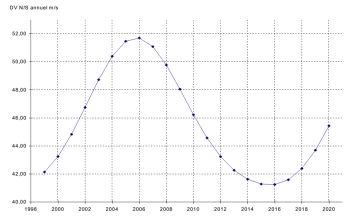
Рис. 5. Годовые затраты ΔV на station keeping геостационарных спутников
Таблица 2
Краткий обзор возмущений на геостационарных орбитах
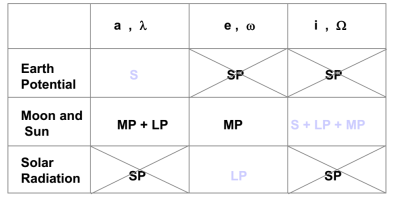
S = светский период
LP = длительные периоды
MP = средние периоды
SP = короткие периоды
Заключение
Орбитальные возмущения геостационарных спутников носят комплексный характер и включают эффекты различной физической природы. Их строгий учёт и регулярное выполнение коррекций орбиты являются необходимым условием долговременной эксплуатации геостационарных космических аппаратов.
Литература:
- Thales Alenia Space. Space Engineering & Operations University. Orbital Perturbations, 2011.
- Montenbruck O., Gill E. Satellite Orbits. Springer, 2000.
- Vallado D. A. Fundamentals of Astrodynamics and Applications. Microcosm Press, 2013.

