Настоящая статья является продолжением работы [1], где рассматривается обобщенная модель Фридрихса 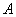 с возмущением ранга не более чем 4, и найдены явный вид существенного и дискретного спектра этого оператора. Там также установлено, что оператор
с возмущением ранга не более чем 4, и найдены явный вид существенного и дискретного спектра этого оператора. Там также установлено, что оператор 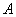 имеет не более чем четыре (с учетом кратности) собственных значений вне существенного спектра. В данной работе мы продолжим изучать спектральных свойств оператора
имеет не более чем четыре (с учетом кратности) собственных значений вне существенного спектра. В данной работе мы продолжим изучать спектральных свойств оператора 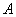 , точнее, описываем строение резольвенты оператора
, точнее, описываем строение резольвенты оператора 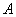 и задача состоит в обосновании этих описаний. При этом используется правило Крамера для системы трех уравнений с тремя неизвестными. Заметим, что обобщенная модель Фридрихса
и задача состоит в обосновании этих описаний. При этом используется правило Крамера для системы трех уравнений с тремя неизвестными. Заметим, что обобщенная модель Фридрихса 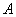 ассоциировано с системой не более чем двух частиц на решетке. Известно, что некоторые актуальные задачи, в частности, задачи квантовой механики, статистической механики и гидродинамики сводятся к исследованию спектральных свойств обобщенной модели Фридрихса [2,3]. Поэтому изучение резольвенты таких операторов играют важную роль в современной математической физике.
ассоциировано с системой не более чем двух частиц на решетке. Известно, что некоторые актуальные задачи, в частности, задачи квантовой механики, статистической механики и гидродинамики сводятся к исследованию спектральных свойств обобщенной модели Фридрихса [2,3]. Поэтому изучение резольвенты таких операторов играют важную роль в современной математической физике.
Пусть 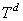 -
- 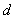 -мерный тор, т. е. куб
-мерный тор, т. е. куб 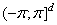 — с соответствующим отождествлением противоположных граней. Всюду в работе
— с соответствующим отождествлением противоположных граней. Всюду в работе 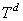 рассматривается как абелева группа в котором операции сложения и умножения на вещественное число введены как операции сложения и умножения на вещественное число в
рассматривается как абелева группа в котором операции сложения и умножения на вещественное число введены как операции сложения и умножения на вещественное число в 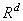 по модулю
по модулю 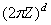 . Здесь через
. Здесь через 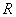 и
и 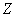 обозначены множество всех вещественных и целых чисел, соответственно.
обозначены множество всех вещественных и целых чисел, соответственно.
Пусть 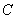 — одномерное комплексное пространство, а
— одномерное комплексное пространство, а 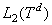 — гильбертово пространство квадратично-интегрируемых (комплекснозначных) функций, определенных на
— гильбертово пространство квадратично-интегрируемых (комплекснозначных) функций, определенных на 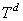 . Обозначим через
. Обозначим через 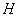 прямую сумму пространств
прямую сумму пространств 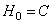 и
и 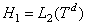 , т. е.
, т. е. 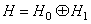 . Пространство
. Пространство 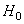 и
и 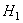 называется нолчастичном и одночастичном подпространством фоковского пространства
называется нолчастичном и одночастичном подпространством фоковского пространства 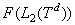 над
над 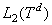 , соответственно.
, соответственно.
Рассмотрим обобщенную модель Фридрихса 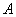 действующую в гильбертовом пространстве
действующую в гильбертовом пространстве 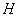 как
как 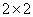 блочно операторная матрица
блочно операторная матрица
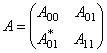 ,
,
где матричные элементы 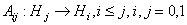 определяются по правилам
определяются по правилам
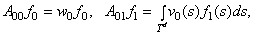
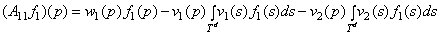 .
.
Здесь 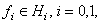
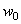 - фиксированное вещественное число,
- фиксированное вещественное число, 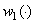 и
и 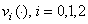 вещественно-непрерывные функции на
вещественно-непрерывные функции на 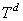 , а
, а 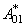 сопряженный оператор к
сопряженный оператор к 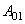 .
.
При этих предположениях оператор 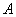 является ограниченным и самосопряжённым в гильбертовом пространстве
является ограниченным и самосопряжённым в гильбертовом пространстве 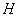 . Надо отметить, что по определению пространства
. Надо отметить, что по определению пространства 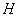 всякий линейный ограниченный оператор в этом пространстве всегда записывается как
всякий линейный ограниченный оператор в этом пространстве всегда записывается как 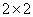 блочно операторная матрица.
блочно операторная матрица.
Обычно оператор 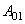 называется оператором уничтожения, а оператор
называется оператором уничтожения, а оператор 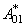 называется оператором рождения [4].
называется оператором рождения [4].
Обозначим через 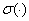 ,
, 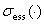 и
и 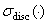 , соответственно, спектр, существенный спектр и дискретный спектр ограниченного самосопряженного оператора.
, соответственно, спектр, существенный спектр и дискретный спектр ограниченного самосопряженного оператора.
Прежде всего дадим краткое информации о спектре оператора 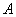 . В работе [1] доказано, что
. В работе [1] доказано, что 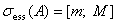 , где числа
, где числа 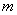 и
и 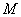 определяются следующим образом:
определяются следующим образом:
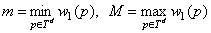 .
.
Определим регулярную в 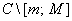 функции
функции
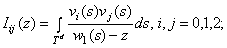
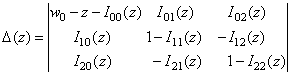 .
.
Очевидно, что функция 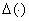 является определителем симметричной матрицы, поэтому нули этой функции являются вещественными. Как было показано в работе [1] для дискретного спектра самосопряженного оператора
является определителем симметричной матрицы, поэтому нули этой функции являются вещественными. Как было показано в работе [1] для дискретного спектра самосопряженного оператора 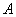 имеет место равенство
имеет место равенство
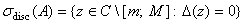 .
.
Учитывая выше сказанные фактов для спектра оператора 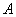 имеем
имеем
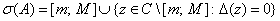 .
.
Теперь переходим к построению резольвенты обобщенной модели Фридрихса 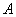 . Для
. Для 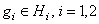 и
и 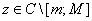 положим
положим
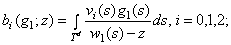
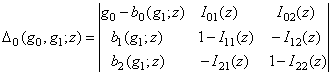 ;
;
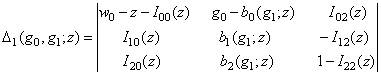 ;
;
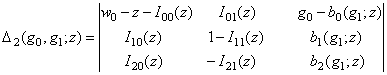 .
.
Сформулируем основной результат работы о явном виде резольвенты обобщенной модели Фридрихса 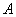 .
.
Теорема. При каждом фиксированном 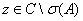 резольвента
резольвента 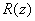 оператора
оператора 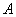 определяется следующим образом:
определяется следующим образом:
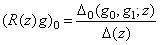 ;
;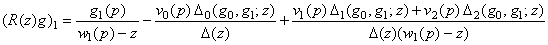 ;
;
где 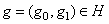 , а
, а 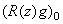 и
и 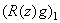 являются компонентами вектора
являются компонентами вектора 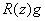 , принадлежащее в
, принадлежащее в 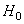 и
и 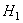 , соответственно.
, соответственно.
Доказательство. Пусть 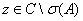 . Для построения резольвенты нам понадобится рассмотреть уравнение
. Для построения резольвенты нам понадобится рассмотреть уравнение 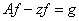 для любых
для любых 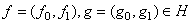 . Для удобства, это уравнение напишем в виде следующей системы уравнений
. Для удобства, это уравнение напишем в виде следующей системы уравнений
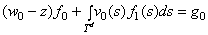 ;
;
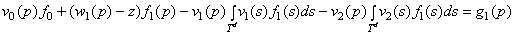 . (1)
. (1)
Для любых  и
и 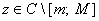 имеет место соотношение
имеет место соотношение 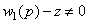 . Тогда из второго уравнения системы (1) для
. Тогда из второго уравнения системы (1) для 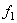 имеем
имеем
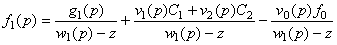 , (2)
, (2)
где
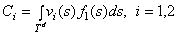 . (3)
. (3)
Подставляя полученное выражение (2) для 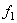 в первое уравнение системы (1) и равенству (3) имеем
в первое уравнение системы (1) и равенству (3) имеем
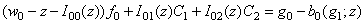 ;
;
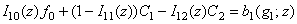 ;
;
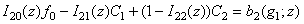 .
.
Так как основной детерминант 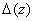 последной системы отлично от нуля при всех
последной системы отлично от нуля при всех 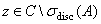 , для таких
, для таких 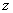 это система уравнений имеет единственный решение
это система уравнений имеет единственный решение 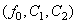 . При этом в силу правила Крамера для системы трех уравнений с тремя неизвестными компоненты
. При этом в силу правила Крамера для системы трех уравнений с тремя неизвестными компоненты 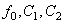 определяются равенствами:
определяются равенствами:
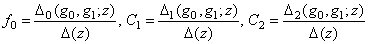 .
.
Далее, подставляя найденные выражения для 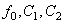 в равенство (2), получим
в равенство (2), получим
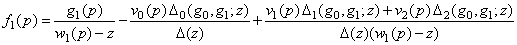 .
.
Сопоставляя полученные выражения для 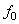 и
и 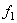 через
через 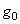 и
и 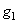 приходим к равенству
приходим к равенству 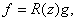 ,
, 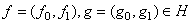 . Теорема доказана.
. Теорема доказана.
Из определения оператора видно, что резольвента 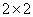 блочно-операторной матрицы опять является
блочно-операторной матрицы опять является 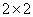 блочно-операторная матрица.
блочно-операторная матрица.
Литература:
1. З. Д. Расулова. О дискретном спектре обобщенной модели Фридрихса с возмущением ранга не более чем 4 // Молодой учёный — 2013 — № 11 — С. 15–17.
2. Л. Д. Фаддеев. О модели Фридрихса в теории возмущений непрерывного спектра // Труды Математического Института АН СССР, 1964, Т. 73, С. 292–313.
3. Р. А. Минлос, Я. Г. Синай. Исследование спектров стохастических операторов, возникающих в решетчатых моделях газа // Теоретическая и математическая физика, 1979, Т. 2, № 2, С. 230–243.
4. К. О. Фридрихс. Возмущения спектра операторов в гильбертовом пространстве. М.: Мир, 1972.

