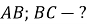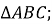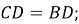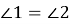В статье рассматривается применение цифрового помощника «Математический конструктор» в обучении геометрии учащихся 7 класса. Описаны функциональные возможности инструмента, его преимущества в визуализации геометрических задач и повышении мотивации учащихся. Представлен разработанный комплекс заданий по теме «Свойства равнобедренного треугольника», включающий алгоритмы построения фигур и решения задач. Результаты исследования демонстрируют эффективность использования цифровых инструментов для улучшения понимания математических концепций и развития логического мышления школьников.
Ключевые слова: цифровые инструменты, математический конструктор, геометрия, равнобедренный треугольник, интерактивное обучение, визуализация .
Введение
Для педагогов математики создан «Математический конструктор» — цифровой помощник, который облегчает работу с математическими задачами, расчетами и уроками. Этот инструмент позволяет быстро формировать и изменять математические формулы, проводить построение геометрических фигур, выполнять числовые расчеты и анализы. Благодаря «Математическому конструктору» создание привлекательных и информативных математических презентаций становится простым и доступным. Преподаватели могут эффективно применять это средство для подготовки к урокам, проведения интерактивных занятий и проверки заданий. «Математический конструктор» помогает сэкономить время, улучшить уровень образования и сделать процесс обучения математике увлекательным и продуктивным.
Новизна представленного исследования заключается в:
- Разработке комплекса заданий по геометрии для 7 класса с использованием «Математического конструктора»
- Предложенные задания включают не только стандартные упражнения, но и интерактивные элементы, позволяющие учащимся экспериментировать с геометрическими фигурами, что способствует более глубокому усвоению материала.
Цель исследования: разработать комплекс заданий по геометрии за 7 класс с применением системы компьютерной математики «Математический конструктор».
Задачи исследования:
- Проанализировать цифровые сервисы, применяемые в практике школьного образования.
- Рассмотреть функциональные возможности СКМ «Математический конструктор» и выделить его преимущества.
- Разработать комплекс заданий по теме «Свойства равнобедренного треугольника» с применением СКМ «Математический конструктор».
Основная часть
В наше время цифровые инструменты становятся неотъемлемой частью образовательного процесса для учащихся. Они обогащают обучение, делая его более интерактивным, удобным и захватывающим для учеников. Важно понимать суть и важность цифровых инструментов, их разнообразие и возможности.
Они включают в себя:
— Интерактивные программы и приложения.
— Онлайн-курсы и электронные учебники.
— Системы дистанционного обучения.
Использование таких инструментов регламентируется федеральными законами и нормативными документами, что подчеркивает их значимость в образовательном процессе. В Республике Татарстан, например, цифровизация активно внедряется, что способствует повышению качества обучения.
«Математический конструктор» — это интерактивная среда, основанная на принципах динамической геометрии. Ее преимущества:
— Визуализация геометрических фигур.
— Возможность создания интерактивных моделей.
— Автоматическая проверка решений.
Программа позволяет учителям легко демонстрировать сложные концепции, а ученикам — экспериментировать с фигурами, что делает обучение более увлекательным и эффективным.
Для темы «Свойства равнобедренного треугольника» были разработаны задания, включающие:
Построение фигур : алгоритмическое предписание построения равнобедренного и равностороннего треугольника в «Математическом конструкторе»
-
Находим на панели управления кнопку

-
Строим равнобедренный треугольник АВС. Выбираем панель

-
Ставим вершины А, В, С. Выбираем панель
-
Отмечаем штрихами стороны и равные углы при основании треугольника

-
Находим снова на панели управления кнопку


-
Отмечаем штрихами стороны треугольника

-
Выбрала на панели управления
Решение задач : например, нахождение сторон треугольника по заданному периметру.
|
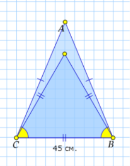
№ 108. «Периметр равнобедренного треугольника ABC с основанием BC равен 40 см, а периметр равностороннего треугольника BCD равен 45 см. Найдите стороны AB и BC». [23, с. 36] | |||
|
Дано: ∆𝐴𝐵𝐶− равнобедренный; 𝑃 𝐴𝐵𝐶 −40 см; 𝐵𝐶−онование. ∆𝐴𝐵𝐶− равносторонний; 𝑃 𝐴𝐵𝐶 =45 см |
|
Решение: 1. Так как ∆𝐴𝐵𝐶 — равнобедренный, то 𝐴𝐵=𝐵𝐶. Значит, его периметр можно записать следующим равенством: 𝑃 𝐴𝐵𝐶 =𝐴𝐵+𝐵𝐶+𝐴𝐶=2𝐴𝐵+𝐵𝐶. 2. Так как треугольник BCD — равносторонний, то 𝐴𝐷=𝐵𝐶=𝐷𝐶; тогда его периметр: 𝑃 𝐵𝐶𝐷 =𝐵𝐷+𝐷𝐶+𝐵𝐶=3𝐵𝐶. Следовательно: 3𝐵𝐶=45; 𝐵𝐶=15 см. 3. Подставим полученные данные в первое равенство и найдем стороны: 𝑃 𝐴𝐵𝐶 =2𝐴𝐵+15=40; 2AB=25; 𝐴𝐵=12,5 см. 𝐴𝐵=𝐴𝐶=12,5 см. Ответ: 𝐴𝐵=12,5 см;𝐵𝐶=15 см | |
|
Найти:
| |||
Доказательство свойств : алгоритмическое предписание построения равнобедренного треугольника в «Математическом конструкторе».
-
Находим на панели управления кнопку

-
Строим равнобедренный треугольник АВС. Выбираем панель

-
Ставим вершины А, В, С. Выбираем панель
-
Отмечаем штрихами равные стороны

Находим снова на панели управления кнопку

-
Ставим вершину D выбирая на панели управления
-
Отмечаем штрихами равные углы 1 и 2 треугольников

-
Выбрала на панели управления

|
№ 112. «На рисунке 65 𝐶𝐷=𝐵𝐷,∠1=∠2. Докажите, что треугольник 𝐴𝐵𝐶 равнобедренный» [23, с. 36] | |||
|
Дано:
|
|
Решение: 1. ∆𝐴𝐵𝐶=∆𝐴𝐷𝐵 по двум сторонам и углу между ними: ∠1=∠2; 𝐴𝐷− общая сторона; 𝐶𝐷=𝐵𝐷 по условию. 2. Так как равные элементы в равных фигурах равны, то получаем: 𝐴𝐶=𝐴𝐵. 3. Следовательно, ∆𝐴𝐵𝐶- равнобедренный. Что и требовалось доказать | |
|
Найти:
| |||
Пример алгоритма построения:
— Выбрать инструмент «Сетка».
— Построить вершины треугольника.
— Отметить равные стороны и углы.
Заключение
Использование «Математического конструктора» в обучении геометрии доказало свою эффективность. Разработанный комплекс заданий позволяет учащимся лучше понимать свойства геометрических фигур, развивает логическое мышление и повышает интерес к предмету. Цифровые инструменты, такие как «Математический конструктор», становятся важным элементом современного образования, способствуя его интерактивности и доступности. Дальнейшие исследования могут быть направлены на расширение комплекса заданий для других тем школьного курса математики.
Литература:
- 1. Александрова Л. В. Методические рекомендации по применению интернет-ресурсов по математике во внеурочной деятельности // Modern Science. 2023. № 3–1. С. 68–71.
- Stepik — образовательная платформа и маркетплейс онлайн-курсов. URL: https://welcome.stepik.org/ru (дата обращения: 06.04.2025).
- Алексеева У. И. К вопросу о применении цифровых технологий при обучении математике // Инновационные технологии в математическом образовании: молодежная парадигма. Сборник научных статей молодых исследователей. Елец, 2023. С. 66–71.
- Официальный сайт ООО «Инфоурок» — курсы, тесты, видеолекции, материалы для учителей. URL: https://infourok.ru/ (дата обращения: 06.02.2025).
- Платформа для онлайн-обучения — создайте онлайн-школу в сервисе и запустите первый курс в конструкторе Skillspace бесплатно. URL: https://clck.ru/3A5AjA (дата обращения: 12.04.2025).
- Бодряков В. Ю. Цифровые лабораторные работы по математике как воплощение когнитивно-деятельностного подхода к обучению будущих учителей // Вестник Ошского государственного университета. Педагогика. Психология. 2023. № 1 (2). С. 42–53.
- Борзенко О. Н. Межпредметная интеграция технологии и математики в школе // Наукосфера. 2023. № 1–2. С. 72–77.
- Боровских А. В. О содержании математического образования. Математика для нематематиков // Continuum. Математика. Информатика. Образование. 2022. № 4 (28). С. 51–65.
- Боталова О. Н. Функциональная грамотность на уроках математики // Молодежная наука в развитии регионов. 2023. Т. 1. С. 370–375.
- СДАМ ГИА: РЕШУ ОГЭ. Математика. URL: https://oge.sdamgia.ru/problem?id=325541 (дата обращения: 26.03.2025).
- Федеральная рабочая программа | Математика. 5–9 классы (базовый уровень). URL: https://cyberleninka.ru/article/n/sozdanie-onlain-kursa-po-vychislitelnom-matematike (дата обращения: 12.03.2025).