В работе изучаются свойства подгрупп конечных групп, определяемые посредством множества
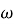
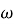
Ключевые слова: группа, конечная группа, класс групп, формация, класс Фиттинга, радикал группы, корадикал группы.
Рассматриваются только конечные группы. Теория классов конечных групп занимает одно из центральных мест в современной алгебре. В настоящее время в рамках данной теории важную роль стали играть подгруппы групп, определяемые с помощью рассматриваемых классов. К таким подгруппам относят
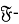
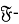

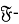





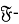

В теории классов групп центральное место занимают локальные формации и классы Фиттинга, естественным обобщением которых являются


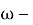

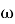
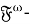
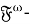
Следуя подходу [2], в настоящей работе введены в рассмотрение понятия
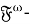
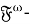
Обозначения и определения, используемые в статье, являются стандартными (см., например, [4]). Приведем лишь некоторые из них.
Через
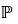
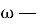
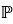
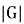


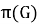



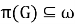
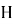



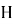

Запись
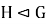
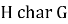
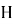

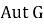

Классом групп называется всякая совокупность групп, которая с каждой своей группой содержит и все группы, ей изоморфные [4, с. 161].
Определение 1.
Класс групп


-
из того, что
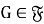
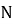


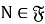
-
из того, что
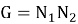
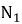
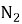


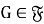
Определение 2.
Пусть


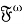




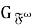
Замечание 1.
Из определения 2 следует, что
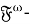



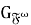

Замечание 2.
Пусть



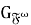



Замечание 3.
В любой группе
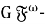
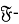
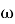
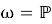
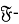
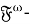

Определение 3. Класс групп 𝔉 называется 𝜔-формацией, если выполняются два условия:
-
если из того, что
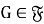
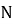


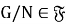
-
если из того, что
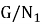
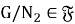
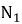
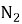


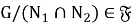
Определение 4.
Пусть


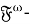




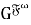
Замечание 4.
Из определения 4 следует, что
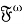



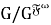

Замечание 5.
Пусть



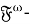




Замечание 6.
В любой группе


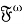
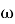
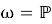

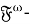

Теорема 1.
Пусть


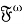
Доказательство.
Пусть

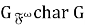
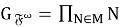
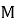



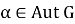
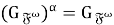
Так как
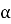


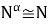
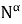



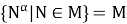
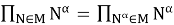
Из определения 2 следует, что
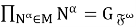
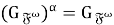
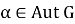
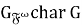
Теорема доказана.
Теорема 2.
Пусть


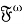
Доказательство.
Пусть

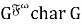
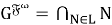
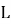



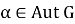
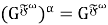
Согласно определению 4, имеет место равенство:
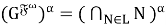

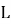
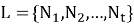
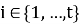
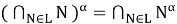
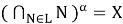
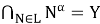
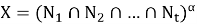
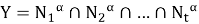
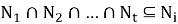
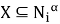
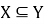
Покажем, что
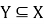
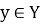
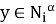
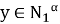
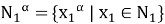
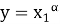
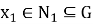
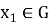
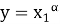
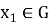
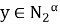
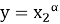
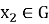
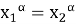
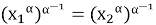
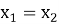
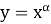
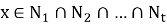
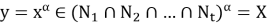
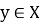
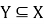
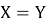
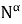


Покажем, что
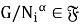
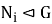
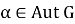
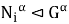
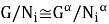
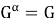
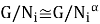
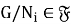

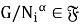
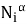



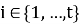
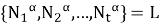
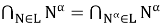
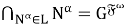
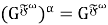
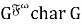
Теорема доказана.
Литература:
- Ведерников, В. А. Элементы теории классов групп / В. А. Ведерников. — Смоленск: СГПИ, 1988. — 96 c.
-
Ведерников, В.А.
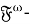
- Воробьёв, Н. Н. Алгебра классов конечных групп / Н. Н. Воробьёв. — Витебск: ВГУ им. П. М. Машерова, 2012. ‒ 322 с.
- Монахов, В. С. Введение в теорию конечных групп и их классов / В. С. Монахов. ‒ Минск: Вышэйшая школа, 2006. — 322 с.
-
Скиба, А. Н. Кратно
-
Сорокина, В. Н. Произведения

- Шеметков, Л. А. Формации конечных групп / Л. А. Шеметков. — М.: Наука, 1978. — 272 с.
- Doerk, K. Finite soluble groups / K. Doerk, T. Нawkes. — Berlin — New York: Walter de Gruyter, 1992. — 901 p.

