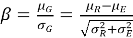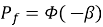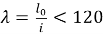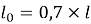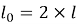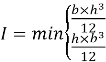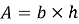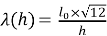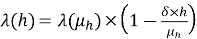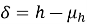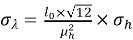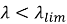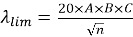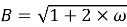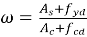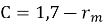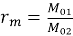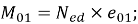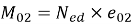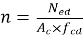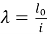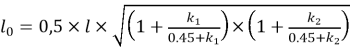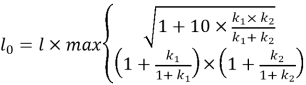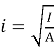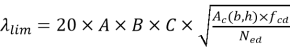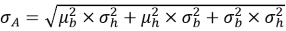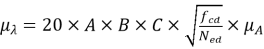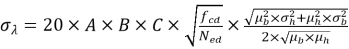В статье рассматривается методика оценки надежности железобетонных конструкций с учетом изменчивости физических свойств материалов и геометрических показателей элемента, в частности внецентренно-сжатых элементов. Изложены теоретические основы и описаны современные подходы к расчету надежности, представлен анализ изменчивости нагрузок и физических характеристик материалов, выполнен сравнительный анализ положений российских и европейских норм в части учета эффектов второго порядка.
Ключевые слова: железобетонные конструкции, метод двух моментов, индекс надежности.
Обеспечение надежности железобетонных конструкций является ключевой задачей современного строительного проектирования. Сложные эксплуатационные условия, а также внедрение новых материалов требуют совершенствования расчетных методик и нормативной базы. Особую актуальность приобретает необходимость сопоставительного анализа российских и европейских норм, особенно в условиях гармонизации стандартов.
Надежность строительной конструкции характеризуется ее способностью сохранять заданные эксплуатационные параметры в течение расчетного срока службы. Она определяется с учетом безопасности, долговечности и эксплуатационной пригодности. В современных подходах к расчету надежности широко применяются вероятностные методы, позволяющие учитывать случайный характер воздействий и отклонений от проектных параметров.
Ключевым показателем надежности выступает индекс β, отражающий обеспеченность конструкции несущей способностью:
|
|
(1) |
где
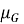
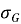
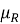

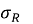
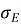
Метод двух моментов, предложенный А. Р. Ржаницыным [4], позволяет аналитически выразить индекс β и оценить вероятность отказа:
|
|
(2) |
где
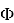
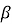
Метод удобен тем, что сводит вероятностные расчеты к оперированию только математическим ожиданием и дисперсией сопротивления и нагрузки. Это делает его применимым в практике проектирования и сравнения нормативных систем.
Метод, предложенный А. Р. Ржаницыным [4], лег в основу метода FORM, который используется в европейской нормативной документации.
В своих исследованиях, посвященных оценке надежности, современные ученые Е. П. Герасимов [1], Д. В. Кузнецов [2], А. С. Махно [3] учитывали влияние изменчивости геометрических параметров железобетонных элементов и пришли к выводу о том, что она сопоставима с изменчивостью прочностных свойств материалов.
В работе В. Д. Райзера [5] приводится аргументация против включения изменчивости геометрических параметров в расчет надежности из-за ее незначительности. В своих публикациях он акцентирует внимание на изменчивости нагрузок и свойств материалов. К такому выводу ученый пришел на основании более неоднородной изменчивости, нежели геометрические параметры.
Согласно российским нормам СП 63.13330.2018 для обеспечения жесткости внецентренно сжатых элементов во всех направлениях должно выполняться следующее условие:
|
|
(3) |
где

i — радиус инерции ядра сечения.
Радиус инерции равен:
|
|
(4) |
где A — площадь сечения колонны;
I — момент инерции сечения.
Расчетная длина подкрановой части колонны:
|
|
(5) |
Расчетная длина надкрановой части колонны:
|
|
(6) |
Так как гибкость зависит от геометрических параметров элемента, можно представить ее в виде функции с учетом изменчивости данных параметров:
|
|
(7) |
Попробуем упростить выражение (7) с учетом того, что момент инерции и площадь сечения можно представить в следующем виде:
|
|
(8) |
|
|
(9) |
Получаем упрощенное уравнение гибкости с учетом изменчивости геометрических параметров сечения:
|
|
(10) |
Из выражения (10) можно сделать вывод, что параметр гибкости зависит только от изменчивости высоты сечения. Таким образом, если отношение
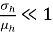
|
|
(11) |
где
|
|
(12) |
Тогда математическое ожидание, гибкость и стандартное отклонение можно представить в следующем виде:
|
|
(13) |
|
|
(14) |
В европейских нормативных документах имеются отличия в отношении учета эффектов второго порядка при расчете сжатых железобетонных элементов, что особенно важно при анализе и обеспечении надежности зданий на стадии проектирования.
Так, согласно пункту 5.8.3 EN 1992 эффекты второго порядка могут не учитываться, если гибкость рассматриваемого элемента меньше значения предельной гибкости:
|
|
(15) |
Предельная гибкость рассчитывается по следующей формуле:
|
|
(16) |
где n — относительное продольное усилие;
А, В, С — коэффициенты, зависящие от ползучести бетона, заданного армирования, внутренних усилий.
В практическом проектировании нахождение эффективного значения коэффициента А довольно трудоемко. Европейские нормы предлагают считать коэффициент А равным 0,7 в случаях, когда уровень ответственности здания относится к нормальному. В рамках данной работы мы определяем уровень ответственности рассматриваемого каркаса как нормальный.
Коэффициент В, согласно европейским нормам, рассчитывается по следующей формуле:
|
|
(17) |
где

|
|
(18) |
где
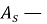
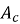


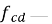
Коэффициент С не имеет граничных значений, что связано со значениями моментов, полученными при статическом расчете. При отсутствии необходимых данных европейскими нормами предусмотрено фиксированное значение коэффициента С, равное 0,7; дополнительно при назначении значения коэффициента необходимо учесть знак момента. При наличии всех необходимых данных коэффициент можно найти по формуле (19):
|
|
(19) |
где
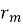
|
|
(20) |
где
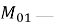
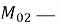
Значения моментов первого порядка у концов надкрановой и подкрановой частей колонны
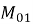
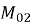
|
|
(21) |
|
|
(22) |
Относительное продольное усилие вычисляется следующим образом:
|
|
(23) |
Гибкость надкрановой и подкрановой частей колонны определяется по формуле:
|
|
(24) |
где
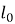
i — радиус инерции ядра сечения.
Расчетная длина подкрановой части колонны определяется по формуле:
|
|
(25) |
где
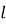
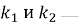
Так как колонна жестко закреплена в фундаменте, то коэффициент
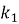
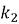
Расчетная длина надкрановой части колонны определяется по формуле:
|
|
(26) |
Для надкрановой части колонны коэффициент
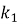
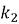
Радиус инерции находим по формуле:
|
|
(27) |
где A — площадь сечения колонны;
I — момент инерции сечения.
Так как гибкость зависит от геометрических параметров элемента, можно представить ее в виде функции с учетом изменчивости данных параметров:
|
|
(28) |
При помощи аппроксимации через разложение Тейлора второго порядка математическое ожидание площади сечения колонны и стандартное отклонение можно представить в виде:
|
|
(29) |
|
|
(30) |
При помощи выражений (29) и (30) и аппроксимации выражения (28) математическое ожидание гибкости и стандартное отклонение примут вид:
|
|
(31) |
|
|
(32) |
Эти формулы позволяют количественно учесть допуски на геометрию и их влияние на надежность конструкции.
Результаты нашего исследования говорят о большей жесткости требований европейских норм при одновременном более полном учете вариации параметров.
На рисунке 1 показана зависимость влияния коэффициента вариации геометрических параметров на индекс надежности.
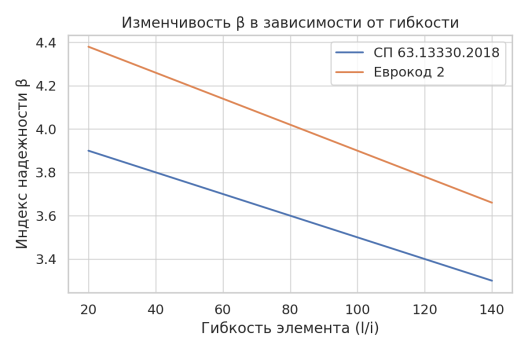
Рис. 1. Зависимость индекса надежности от изменения геометрических параметров
Итак, мы рассмотрели вероятностный подход к оценке надежности внецентренно сжатых железобетонных элементов с учетом изменчивости геометрических параметров. Использование метода двух моментов позволяет значительно упростить расчеты и в упрощенной форме оценить зависимость индекса надежности от статистических характеристик сопротивления и нагрузок.
Сравнительный анализ европейских и российских норм показал, что первые обеспечивают более полный учет изменчивости параметров.
Литература:
- Герасимов, Е. П. К вопросу нормирования надежности по деформациям железобетонных изгибаемых конструкций / Е. П. Герасимов // Вестник Томского государственного архитектурно-строительного университета. — 2019. — Т. 21, № 5. — С. 115–126.
- Кузнецов, Д. В. Надежность внецентренно сжатых железобетонных элементов при расчете по прочности нормальных сечений: дис. … кандидата технических наук: 05.23.01 / Д. В. Кузнецов. — М., 2012. — 187 с.
- Махно, А. С. Надежность изгибаемых железобетонных элементов по нормальным сечениям, усиленных бетоном и арматурой: дис. … кандидата технических наук / А. С. Махно. — М., 2005. — 174 с.
- Ржаницын, А. Р. Теория расчета строительных конструкций на надежность / А. Р. Ржаницын. — М.: Стройиздат, 1978. — 239 с.
- Райзер, В. Д. Теория надежности в строительном проектировании / В. Д. Райзер. — М.: АСВ, 1998. — 304 с.