Рассмотрена комбинаторная проблема подсчета числа перестановок с ограничениями. Приведены практические задачи, сводящиеся к задаче о беспорядках. Представлено разработанное программное средство для вычисления рассматриваемых комбинаторных чисел.

Ключевые слова: комбинаторика, перестановки, число беспорядков.

Изучение основных правил комбинаторики традиционно завершается рассмотрением метода включений и исключений. Иллюстрацией применения этого метода является так называемая задача о беспорядках.

Исторически первой задачей подобного рода является задача Эйлера.

Задача Эйлера. Войдя в ресторан, n гостей оставили швейцару свои шляпы, а на выходе получили их обратно. Швейцар раздал шляпы случайным образом. Сколько имеется вариантов, в которых каждый гость получил чужую шляпу?

В общем виде задача формулируется следующим образом: рассмотрим перестановки n различных предметов, при которых ни один предмет не стоит на своём первоначальном месте. Такие перестановки называются беспорядками , смещениями или субфакториалами . [1]

Число их можно найти по формуле включений и исключений

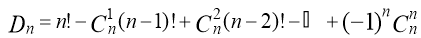
Проделав ряд преобразований, можно представить эту формулу в таком виде:

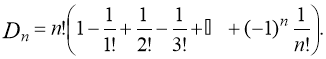
Такие комбинаторные числа обладают рядом свойств. Например, известна рекуррентная формула

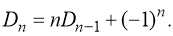
Можно привести также другую рекуррентную формулу для числа беспорядков:

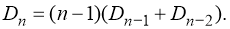
Ослабим требование задачи и разрешим некоторым элементам оставаться на своем месте.

Перестановки n различных предметов, при которых ровно k предметов стоят на своих первоначальных местах, называют перестановкой с k встречами . Количество их выражается числом

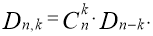
Задача. Рассеянный почтальон должен разнести 10 писем по 10 адресам. Сколькими способами он может разложить письма по почтовым ящикам так, чтобы а) ни один адресат не получил адресованное ему письмо; б) ровно 5 человек получили адресованные им письма? [2]

Решение.

а) Искомое число способов равно

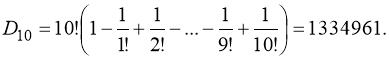
б) Искомое число способов равно

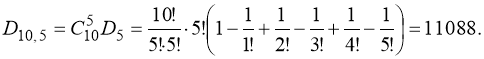
Задача. Сколько существует перестановок различных предметов, при которых на своих первоначальных местах окажутся ровно 2 или ровно 6 предметов?

Решение. Количество различных перестановок девяти предметов, при которых на своих первоначальных местах окажутся ровно 2 предмета, равно а количество различных перестановок девяти предметов, при которых на своих первоначальных местах окажутся ровно 6 предметов, равно Применяя правило суммы, а также формулу для вычисления , имеем:

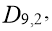
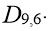
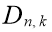
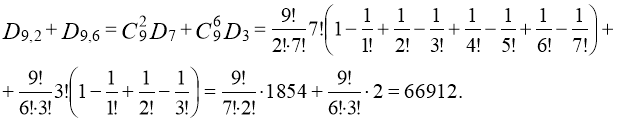
Приведем еще несколько практических содержательных задач, решение которых сводится к нахождению числа беспорядков или перестановок со встречами.

Задача. Две колоды карт, одну из которых заранее перетасовали, сравниваются карта за картой. Какова вероятность, что за все время просмотра не встретится ни одного совпадения?

Задача. Профессор дал четверым студентам контрольную работу, а затем предложил проверить ее друг у друга. Ни один студент не может проверять свою работу. Сколько имеется вариантов распределения работ?

Задача. Группа из 12 студентов играют в «Тайного Санту». Сколько имеется вариантов распределения подарков, если никто не должен получить собственный подарок?

Задача. Девять художников представили свои картины на выставке. Каждая картина имеет номер, соответствующий номеру художника. Для шуточного конкурса решено изменить расположение картин, чтобы заставить зрителей гадать, где чья работа. С учетом условия, что максимум две картины могут остаться на своем месте, сколько существует способов переорганизовать выставку?

Так как значения этих комбинаторных чисел зависят не от конкретной задачи, а только от параметров n и k , их можно вычислить и свести в таблицу (см. табл. 1). В этом случае получаем хорошую задачу для тех, кто делает первые шаги в программировании.

Таблица 1

Числа беспорядков и перестановок с k встречами

Для вычисления числа беспорядков была разработана программа на языке С. Блок-схема ее представлена на рисунке 1.

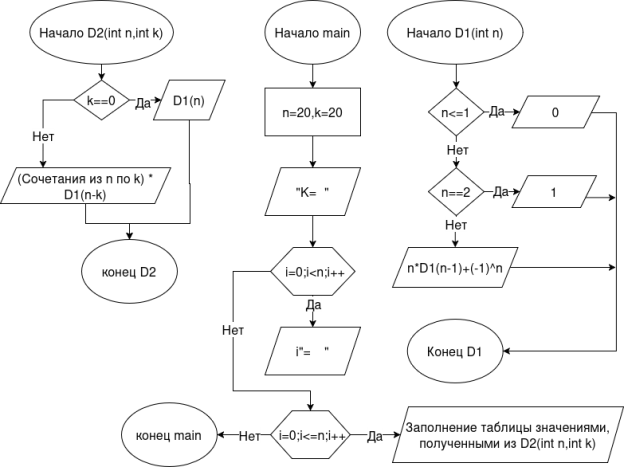
Рис. 1. Блок-схема программы вычисления числа беспорядков

При тестировании программы было установлено, что до значений n = 20 программа работает корректно. При увеличении значений n до 21 и выше, значение факториала, необходимого для подсчёта количества сочетаний, превысит значение 64 бита для переменной (это превышение типа данных long long). Поэтому для работы c n  21, если используется язык C, нужно использовать специальные библиотеки (GMP) или другие алгоритмы (расширения компиляторов GCC, CLANG для 128-битных значений).

Литература

1. Виленкин Н. Я., Виленкин А. Н., Виленкин П. А. Комбинаторика: учебное пособие. — М.: «ФИМА» МЦНМО, 2023.
2. Тишин В. В. Дискретная математика в примерах и задачах: учебное пособие. — СПб.: БХВ-Петербург, 2008.