В работе
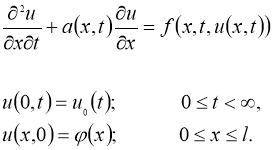
В данной работе рассматриваем следующую задачу:
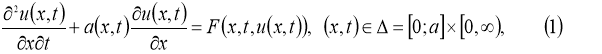

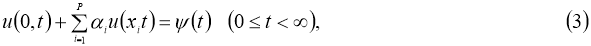
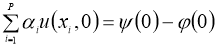
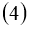
и находятся достаточные условия однозначной разрешимости и непрерывная зависимость решений от параметров, где
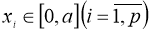
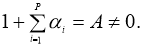
1. Однозначная разрешимость решения задачи (1) — (4)
Для однозначной разрешимости задачи
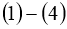
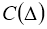
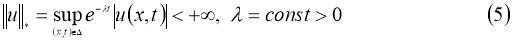
Теорема
1.
Пусть функции
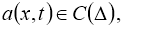
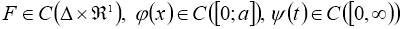
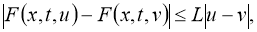
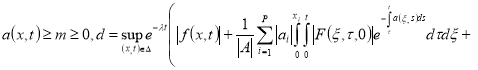
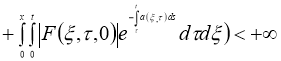
где
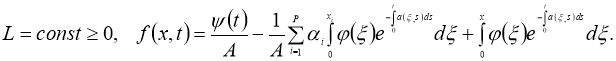
Если сушествует
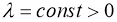
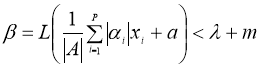
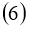
тогда задача (1) — (4) имеет единственное решение в пространстве
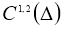
Доказательство. Задача (1)–(4) эквивалентна интегральному уравнению
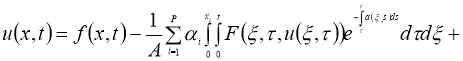

Правую часть уравнения
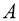
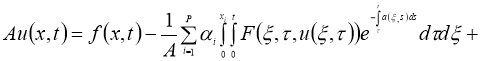
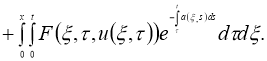
Докажем, что
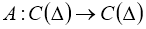
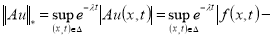
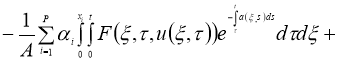
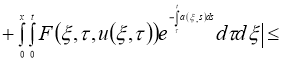
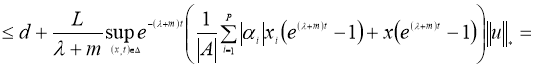

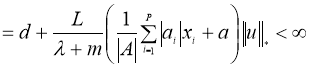
Теперь докажем, что оператор
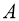
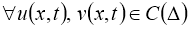
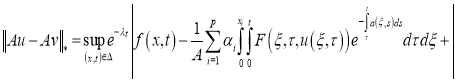
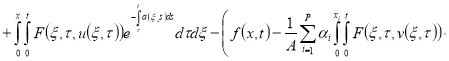
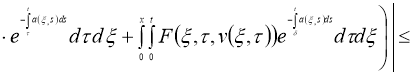
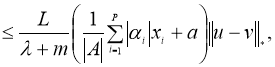
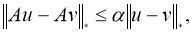
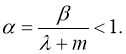
Доказательство теоремы следует из принципа сжимающих операторов.
2. Непрерывная зависимость решений от параметров
Теперь рассмотрим следующие задачи:
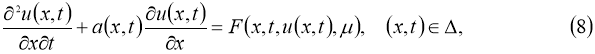

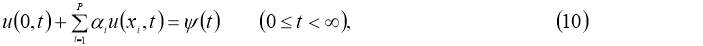

где
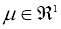
Теорема
2.
Пусть функции
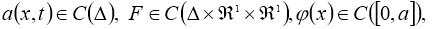
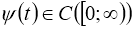
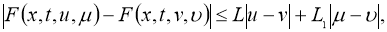
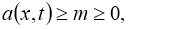
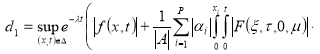
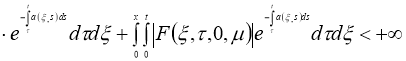
где
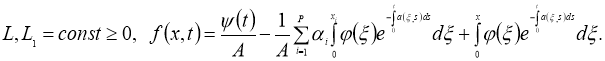
Если существует
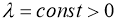
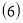
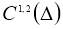
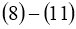
Доказательство.
При фиксированной
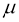
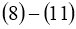
Задача
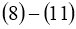
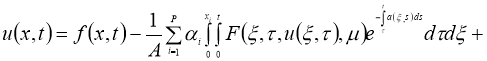

Обозначим через
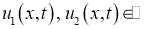
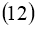
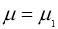
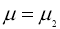
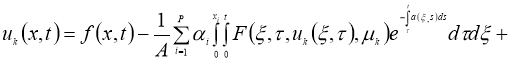
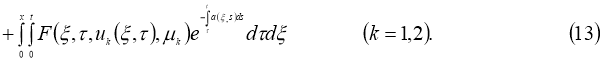
Используя условия теоремы 2 из уравнения
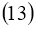
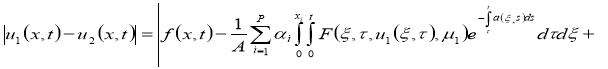
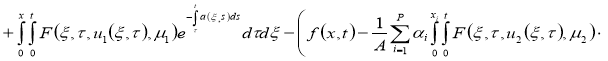
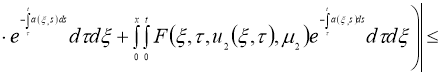
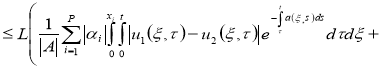
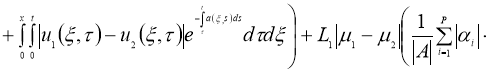
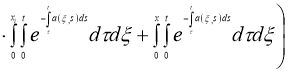
Используя норму
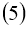
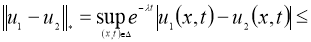
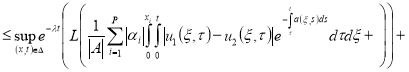
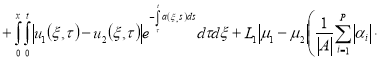
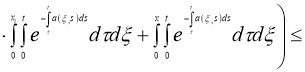
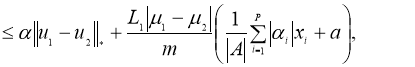
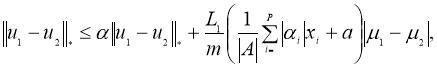

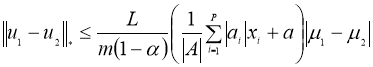
Отсюда следует утверждение теоремы 2.
Теоремы 1, 2 верны для следующих задач:
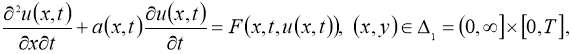
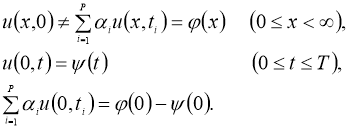
Литература:
- Shan S. M. On the exponential Growth of solutions to non-linear hyperbolic eQuations //Internat.J.Math. u Math.Sci.Vol. 12. №.3 (1989) 539–546.

