Решение некоторых задач нелинейной теории упругости с помощью пакета Maple



Одним из распространенных пакетов символьных вычислений является Maple. В основном этот пакет ориентирован на символьное вычисление и численную составляющую [1,2]. Актуальной задачей является разработка проблемно специализированной системы расчетов являющейся комбинацией численных и символьных методов вычислений на базе Maple, ориентированной на применение в нелинейной теории упругости. Создание специализированной системы расчетов позволяет использовать мощные средства символьного интегрирования, методов минимизации функционалов, возможностей визуализации результатов, присущих Maple. Символьная составляющая позволяет написать программу численного интегрирования для функций с параметрами, значения которых не заданы. Поэтому появляется возможность вычислить интегралы в функционалах при итерационных методах минимизации только один раз. Этот подход позволяет избежать вычисления интегралов на каждом шаге итерационного процесса. Одноразовость интегрирования позволяет обходиться простейшими формулами численного интегрирования.

Ключевые слова:численно-символьное интегрирование, антиплоская деформация, вариационный принцип, неогуковский потенциал.

Одним из распространенных пакетов символьных вычислений является Maple. Рассматриваемый пакет применяется не только для теоретических исследований, но и содержит численную составляющую, что расширяет сферу его применения. Актуальной задачей является разработка проблемно специализированной системы расчетов являющейся комбинацией численных и символьных методов вычислений на базе Maple [3,4], ориентированной на применение в нелинейной теории упругости [5,6]. То, что специализированная система создается на базе Maple, диктует ее конфигурацию в виде библиотек авторских программ, подгружаемых в Maple пользователем и структуру интерфейса в виде рабочего листа Maple. Подгружаемые библиотеки, могут быть отнесены к алгоритмическим подсистемам, а содержащиеся в них программы к символьным и численным блокам в составе универсальной САВ (системы аналитических вычислений), в качестве которой выступает Maple. Все программы написаны на внутреннем языке программирования пакета Maple. Для краткости комбинированную символьно-численную систему вычислений будем обозначать СЧС [4]. Данная система не является альтернативной для известных численных пакетов типа ANSYS, ABAQUS и подобных. Она просто расширяет возможности пакета Maple, упрощая его применение в задачах механики.

Создание сложных универсальных программных средств, призванных решать множество задач требует огромных интеллектуальных, временных и материальных затрат. Представляется более эффективным использование простых моделей, решающих конкретные задачи [7–9]. Совокупность алгоритмических подсистем для решения таких задач может составить автоматизированное рабочее место механика в среде Maple.

В линейной теории упругости, из трехмерных задач, выделены двухмерные задачи с осесимметричной, плоской и антиплоской деформацией. Последний вид деформации наиболее простой, поэтому естественно начать с модели антиплоской деформации. В нелинейной теории упругости проблема такого разделения более сложная. Так для несжимаемых материалов антиплоская деформация возможна только в телах с потенциалами энергии деформации, удовлетворяющими условиям, сформулированным в [10]. Например, она всегда возможна в материалах с обобщенным неогуковским потенциалом. Литература, посвященная нелинейной антиплоской деформации обширна [11–18].

Естественным практическим приложением конечной антиплоской деформации является расчетная модель резинометаллического амортизатора продольного сдвига [19–21]. Резинометаллические амортизаторы сдвига обычно состоят из металлических (плоских, трубчатых или фасонных) обойм, между которыми прочно закреплена резина. Обоймы сдвигаются относительно друг друга, обеспечивая антиплоскую деформацию резинового массива на достаточном удалении от торцов. То есть рассматриваются длинные амортизаторы. Следует отметить, что при антиплоской деформации объем сохраняется независимо от того сжимаемый материал или несжимаемый, якобиан преобразования равен единице для любой функции депланации поперечного сечения, задающей эту деформацию. Это геометрическое свойство самой деформации. Выбрана модель несжимаемого материала, поскольку она наиболее разработана. Следует отметить и то, что применение фасонных обойм предполагает разнообразие конфигураций поперечного сечения, которое может быть достаточно сложным.

Функциональные свойства СЧС

– СЧС предназначена для приближенного решения любых статических задач при конечной антиплоской деформации со смешанными граничными условиями и произвольным неогуковским потенциалом для областей со сложной конфигурацией. В частности, она позволяет автоматизировать расчет резинометаллических амортизаторов сдвига при конечных деформациях, со свободным вводом любого неогуковского потенциала и достаточно сложной конфигурацией поперечного сечения амортизатора.

– Реализует смешанный вариационный принцип, для которого граничные условия являются естественными, что упрощает алгоритм аппроксимации искомых функций.

– Предоставляет выбор способа аппроксимации искомых функций ортогональными многочленами разного вида с учетом симметрии задачи во всей заданной области. Такая нелокальная аппроксимация при приемлемой точности позволяет на порядок снизить время счета по сравнению с адаптивными аппроксимациями МКЭ и другими подобными методами. При этом производится апостериорная оценка точности решения путем оценки величины невязок уравнений в различных функциональных нормах. Невязка граничных условий оценивается с помощью равномерной нормы, невязка дифференциальных уравнений с помощью энергетической нормы.

– Система нелинейных алгебраических уравнений, полученная при декомпозиции условий стационарности функционала вариационного принципа, решается методом наименьших квадратов, который исключает появление комплексных корней, не имеющих физического смысла, но иногда появляющихся в силу приближенности самой системы уравнений.

– Учет геометрической информации производится с помощью R- функций [22–24]. Такой подход упрощает задание конфигурации области определения искомых функций, граничных условий и позволяет автоматизировать вычисление кратных интегралов для сложных областей.

– Программная реализация алгоритмов выполнена на внутреннем языке программирования Maple.

– Интерфейс и средства визуализации используются из пакета Maple.

В основу программной реализации пакета СЧС положен модульный принцип организации, обеспечивающий возможность модернизации расчетных модулей и реализации новых возможностей, путем подключения к пакету дополнительных модулей. Одним из модулей является модуль символьно-численного интегрирования, применяемый при вычислении интегрального функционала.

Численно-символьное интегрирование

Символьный пакет позволяет написать программу численного интегрирования для функций с параметрами, значения которых не заданы. Поэтому появляется возможность вычислить интегралы в функционале только один раз. То есть, если неизвестные функции аппроксимируются заданными функциями вида u=u(x,y,c1,c2,…cn) где ck не заданы, то после численного интегрирования функционал превращается в числовую функцию только переменных F(c1,c2,…cn), необходимым условием стационарности которой, является система:

. (1)

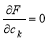
Этот подход позволяет избежать вычисления интегралов на каждом шаге итерационного процесса, что было бы неизбежным при численном интегрировании, поскольку в последнем случае значения коэффициентов необходимо задавать, а они меняются на каждом шаге. Одноразовость интегрирования позволяет обходиться простейшими формулами численного интегрирования, поскольку нет технических препятствий для значительного увеличения числа узлов квадратурной формулы. Интегрирования по границе области и внутри области не связаны друг с другом и количество узлов в квадратурных формулах для границы и области тоже не связаны.

Вычисление криволинейных интегралов сводится к определенному интегралу, который вычисляется модулем

. Здесь -подынтегральная функция, — нижний и верхний пределы интегрирования, а -число узлов квадратурной формулы. В качестве квадратурной формулы используется среднее значение формул левых, правых и средних прямоугольников:

(2)

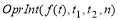
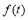
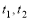
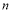
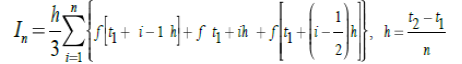
в которой все вычисления проводятся в символьном виде. В приложении 1 приводятся примеры использования модуля . Показано монотонное повышение точности с ростом числа узлов в соответствие с известной оценкой для функций с ограниченной производной порядка не ниже второго [7,25 ]. Далее продемонстрирован результат интегрирования выражения с неопределенными коэффициентами модулем СЧС, которое не интегрируется символьно и средствами численного интегрирования Maple. Двойные интегралы по прямоугольной области вычисляется модулем . Здесь -подынтегральная функция,

— границы изменения x , - границы изменения y , а n -число узлов квадратурной формулы по одной переменной, то есть общее количество узлов . Квадратурная формула используется в виде:

(3)

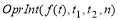
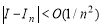
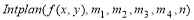
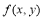
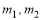
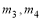
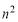
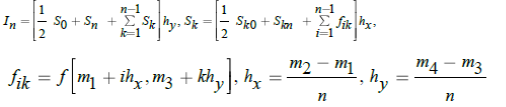
то есть последовательно использована формула трапеций. В приложении 2 приводятся примеры использования модуля. . При интегрировании по прямоугольнику показано монотонное повышение точности с ростом числа узлов для функций с ограниченными частными производными порядка не ниже второго. Далее, в приложениях 3–5 продемонстрирован результат интегрирования по криволинейной области. Как уже отмечалось, интегрирование проводится модулем по прямоугольнику, но подынтегральная функция умножается на индикатор фигуры. Здесь возникает проблема заполнения прямоугольника точками фигуры. Чем сильнее площадь фигуры отличается от площади прямоугольника при неизменном диаметре фигуры, тем меньше точность интегрирования с помощью индикатора. Решение проблемы основано на аддитивности интеграла. Фигура покрывается элементарными прямоугольниками так, чтобы разность площадей элементарных фигур и элементарных прямоугольников была малой. Интегрирование ведется по каждому прямоугольнику, а результаты суммируются. В приложениях 6 продемонстрирован пример при разбиении исходного прямоугольника на четыре части. Далее, в приложении 7 приводится пример интегрирования выражения с неопределенными коэффициентами модулем СЧС, которое не интегрируется символьно и средствами численного интегрирования Maple.

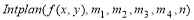
Приложение1

Приложение2

Приложение3

Приложение4

Приложение 5

Приложение 6

Приложение 7

Заключение (выводы)

На основе совокупности численных и символьных методов реализована процедура вычисления интегралов от функций, содержащих неопределенные параметры. Это позволяет производить интегрирование один раз и получить выражение для функционала как функции от коэффициентов аппроксимационных многочленов.

Литература:

1. Системы аналитических вычислений (методы компьютерной алгебры) в механике деформируемого твердого тела. Докл. Всес. совещ. Киев, 1988. — КГУ. Киев, 1990, (168с.) Деп. УкрНИИНТИ 17.04.90, № 732, — Ук90.
2. Системы для аналитических преобразований в механике // Тезисы докладов Всесоюзн. совещания. Горький: ГГУ, 1984. 147 с.
3. Жуков, Б. А. Проблемно специализированная система автоматизированных вычислений «Рабочее место механика». / Б. А. Жуков; Волгогр. гос. пед. ун-т. Волгоград, 2006. 20 c. Деп. в ВИНИТИ 19.10.06, № 1250-В2006.
4. Ю. Ю. Андреева, Б. А. Жуков . Комбинированная система численных и символьных методов на базе MAPLE в задачах нелинейной антиплоской деформации // Вычислительная механика сплошных сред. — 2016. — Т. 9, № 2 (апрель-июнь). — C. 237–244.
5. Зубов Л. М. Принцип стационарности дополнительной работы в нелинейной теории упругости. // ПММ, 1970. Т. 34, № 2. С. 241–245.
6. Зубов Л. М. Вариационные принципы нелинейной теории упругости. // ПММ.1971. Т. 35, № 3. С. 406–410.
7. Бондарь В. Д.. Моделирование нелинейного антиплоского деформирования цилиндрического тела.//ПМТФ.2005.Т.46,№ 4. С.99–109.
8. Черных К. Ф. Нелинейная теория упругости в машиностроительных расчетах. Л.: Машиностроение, 1986. 335с.
9. Яворский Ю. Резина в автомобилях. Л.:Машиностроение, 1980. 360 с.
10. Gent, A.N., Thomas, A. G. J., Polymer Science, Vol. 28, pp. 625, 1958.
11. Жуков, Б. А. Нелинейное взаимодействие конечного продольного сдвига и конечного кручения втулки из резиноподобного материала. // Известия РАН. Механика твёрдого тела. 2015. № 3.C. 127–135.
12. De Pascalis R., Destrade M., Saccomandi G. The stress field in a pulled cork and some subtle points in the semiiinverse method of nonlinear elasticity. / Proc. R. Soc. A (2007). P. 463.
13. Жуков Б. А. Нелинейный эффект взаимодействия плоских и антиплоскостных деформаций в несжимаемом материале // Современные проблемы механики сплошной среды.4-я Международная конференция: Ростов;1998. 142–145 с
14. Horgan C. O. Anti-Plane Shear Deformations in Linear and Nonlinear Solid Mechanics.//SIAM Review, 1995, Vol. 37, No. 1. P. 53–81 .
15. Horgan С, Saccomandi G. Superposition of generalized plane strain on anti-plane shear deformations in isotropic incompressible hyperelastic materials. Journal of Elasticity. 2003;73(1–3):221–235.
16. Knowles J. K. On finite anti — plan chare for incompressible elastic materials // J. Austral. Math. 1976. B19. ¹4. P. 400–415.
17. Knowles J. K. A note on anti-plane shear for compressible materials in finite elastostatics.//J. Austral. Math. Soc. 1977, B20. P. 1- 7.
18. Knowles J. K. The fjnite anti-plane sheared near the tip of a crack for a class of incompressible elastic solids. // Internat. J. Fracture, (1977b), 13, pp. 611–639.
19. Черных К. Ф., Шубина И. М. Законы упругости для изотропных несжимаемых материалов, феноменологический подход. // Механика эластомеров. Краснодар. 1978. Т. 2. Вып. 268. С. 56–62.
20. Черных К. Ф. Нелинейная теория упругости в машиностроительных расчетах. Л.: Машиностроение, 1986. 335с.
21. Черных К. Ф., Литвиненкова З. Н. Теория больших упругих деформаций. Л.: Изд-во Ленингр. ун-та, 1988. 254 с.
22. Рвачев В. Л., Слесаренко А. П. Алгебра логики и интегральные преобразования в краевых задачах. Киев. Наукова Думка 1976. 289 с.
23. Рвачев В. Л., Синекоп Н. С. Метод - функций в задачах теории упругости и пластичности. Киев. Наукова Думка 1990. 212 с.
24. Рвачев В. Л., Шейко Т. И. Введение в теорию - функций. //Проблемы машиностроения, 2001. Т. 4, № 1–2. С. 46–58.
25. Болотин В. В. Нелинейная теория упругости и устойчивость «в большом». // Расчеты на прочность в машиностроении. М.: Машгиз.1958. № 3. С.