Рассмотрен метод построения вывода в экспертной системе на основе правила Байеса. Разработана демонстрационная программа в виде web-приложения с применением стека технологий java и spring. Данная программа позволяет на практике убедиться в работоспособности данного метода и закладывает фундамент для дальнейшего исследования и развития данной работы.

Ключевые слова: теорема Байеса, вывод Байеса, экспертная система.

Теорема Байеса многим известна из теории вероятностей [2], и записывается в виде:

, где:

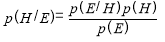
— H — представляет определенную гипотезу, которая может быть, а может и не быть некоторой нулевой гипотезой;

— P(H) — называется априорной вероятностью H, которая была выведена прежде, чем новое свидетельство E стало возможным;

— P(E/H) — называется условной вероятностью наблюдения свидетельства Е, если гипотеза H оказывается верной; её также называют функцией правдоподобия, когда она рассматривается как функция H для фиксированного E;

— P(E) — называется маргинальной вероятностью E: априорная вероятность наблюдения поступившего свидетельства E согласно всем возможным гипотезам; может быть вычислено по формуле полной вероятности.

Распишем P(E) так будет более удобно для дальнейшей работы:

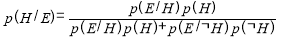
Для уменьшения количества вычислений удобно рассматривать события E ₁ и E ₂ как условно независимыми, таким образом их совместная вероятность когда некоторая гипотеза H окажется верна, будет равна произведению условных вероятностей этих событий при условии H:

.

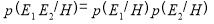
Теперь перейдем в формуле Байеса к случаю множественных гипотез (H ₁ ,…,H _m ) и множественных свидетельств (E ₁ ,…,E _n ). Вероятности каждой из гипотез при условии возникновения некоторого конкретного свидетельства E можно определить из выражения:

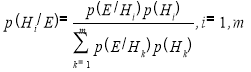
А в случае множественных и независимых свидетельств:

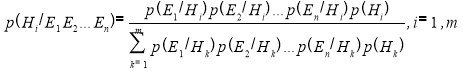
Теперь, переходя к терминологии предметной области данной работы заменим: гипотезы H _k на диагнозы D _k , а свидетельства E _k на симптомы S _k , и немного перепишем формулу в виде удобном для программной реализации, получим:

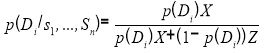
, где при этом ;

при этом .

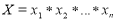
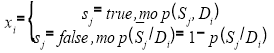
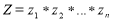
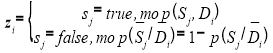
Таким образом байесовский вывод сведется к многократному вычислению двух типов условных вероятностей:

(1)

(2)

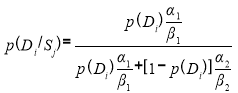
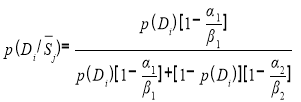
, где: ;

.

В разрабатываемой программе примем начальное значение для всех диагнозов p(D _i ) = 0,5. И основной алгоритм байесовского вывода для расчета вероятности конкретного диагноза для определенного пациента примет вид:

1. Взять все симптомы пациента, обозначим через А;
2. Взять все симптомы, которых у пациента нет, обозначим через В;
3. for(a: A) вычисляем p(D _i ) = (1);
4. for(b: B) вычисляем p(D _i ) = (2);
5. Ответ: p(D _i ) и будет являться вероятностью данного диагноза.

Данные шаги повторить для всех диагнозов из базы знаний экспертной системы. И взять диагноз с самой высокой вероятностью. Он и будет ответом системы.

Программными технологиями для реализации экспертной системы были выбраны: Java совместно с фреймворком Spring для сервера и Angular для фронтенд части приложения, используемые версии: Java 17, Spring 5 и Angular 13. Данные технологии являются распространенными промышленными стандартами в разработки ПО и было интересно протестировать их для разработки ЭС. Разработанная система представляет собой клиент серверное приложение. С четким разделением обязанностей согласно архитектурному паттерну Model-View-Controller.

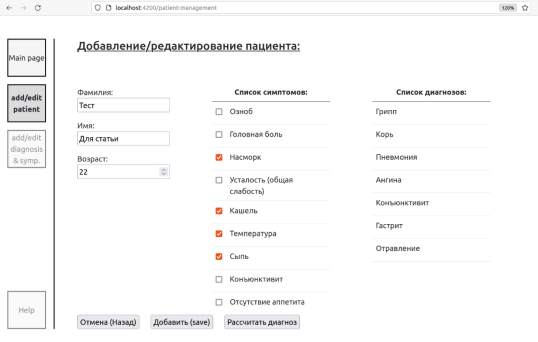
Рис. 1. Окно приложения для работы с пациентом и его диагнозом

Реализация ЭС как Web-приложения позволяет работать с ней из любого места и с любого устройства, на котором установлен браузер. На данный момент приложение при работе с UI поддерживать все CRUD (create, read, update, delete) операции над пациентами, симптомами и диагнозами. А также позволяет запускать механизм байесовского вывода при выборе определенных симптом.

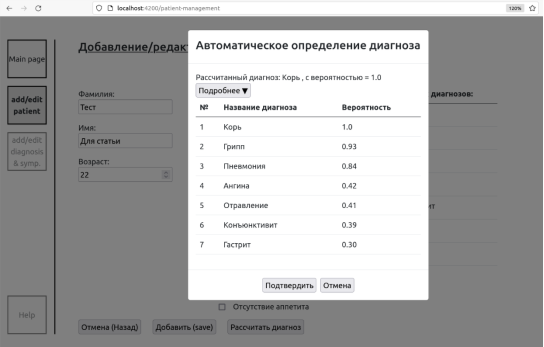
Рис. 2. Модальное окно с результатом байесовского вывода

В качестве примера рассмотрим страницу для работы с данными пациента. На данной странице есть возможность работать с личными данными пациента, выбрать его симптомы и установить диагноз. После выбора симптом и клика по кнопке “Рассчитать диагноз” инициируется процесс байесовского вывода и всплывает модальное окно с результатами вывода , которые можно принять или отклонить, выбрав диагноз из списка вручную.

Рис. 3. Пример байесовского вывода для одного диагноза одного пациента

Для проведения эксперимента была составлена база знаний из семи диагнозов и их симптом. Всего 24 симптома. И на основе данных по болезням было сгенерировано 350 пациентов.

Генерация представляла собой следующую последовательность действий: берем диагноз и все симптомы с ним связанные, затем случайным образом выбирали случайное кол-во (больше нуля) симптом данного диагноза. И с вероятностью в 10 % добавляли случайный симптом, который не принадлежит диагнозу.

Следующий шаг, расчет диагнозов для всех пациентов. Пример байесовского вывода для одного диагноза одного пациента приведен на .

Затем были добавлены ещё 50 пациентов, и повторно рассчитаны диагнозы для пациентов. В ходе данного вычислительного эксперимента система показала точность в 96.7 %. Что говорит о достаточной эффективности данного подхода.

Литература:

1. С. П. Хабаров “Интеллектуальные информационные системы” [лекции] СПЛА — Санкт-Петербург 2007 — С. 181
2. Байесовский вывод [Электронный ресурс]: (дата обращения: 05.02.2022) https://science.fandom.com/ru/wiki/Байесовский_вывод (дата обращения: 05.02.2022)
3. Хорстманн, Кей С. Java. Библиотека профессионала, том 1. Основы. 11-е изд.: Пер. С англ. — СПБ.: ООО “Диалектика”, 2019. — 864 с.
4. Руководство по Angular 13 [Электронный ресурс]: https://metanit.com/web/angular2 (дата обращения: 10.02.2022).