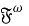В статье изучаются свойства подгрупповых m-функторов. Доказывается критерий ωрегулярности подгруппового m-функтора, а также устанавливается взаимосвязь решетки всех ωрегулярных подгрупповых m-функторов с решеткой всех ωпримитивных классов конечных групп.
Ключевые слова: конечная группа, класс групп, подгрупповой m-функтор, ωпримитивный класс групп.
Рассматриваются только конечные группы. В настоящее время такие направления современной алгебры, как теория подгрупповых функторов и теория классов конечных групп, являются интенсивно развивающимися и тесно связанными между собой (см., например, [3]). Среди подгрупповых функторов важное место занимают подгрупповые m- функторы, которые сопоставляют каждой группе совокупность всех или некоторых максимальных подгрупп данной группы. Наиболее значимые результаты о свойствах подгрупповых m- функторов получены М. В. Селькиным, Р. В. Бородичем и другими алгебраистами (см., например, [6]).
В работе С. В. Каморникова [2] изучены регулярные подгрупповые
m-
функторы и установлена их связь с примитивными классами групп. Естественным обобщением регулярных подгрупповых функторов являются
ω
регулярные подгрупповые функторы, где
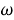
Целью данной работы является исследование
ω
регулярности подгруппового
m-
функтора. Решены следующие задачи: установлена
ω
регулярность
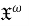
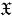
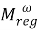
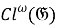
Используемая терминология стандартна (см., например, [3, 5]). Приведем некоторые из них:
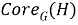
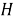

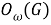

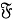
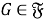
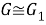
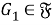
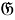
Пусть
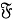
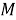

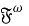

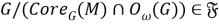


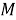
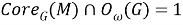
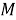

Отображение
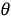

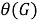
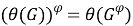
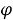

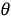

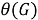

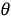

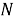
1)
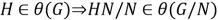
2)
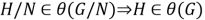
Подгрупповой
m-
функтор назовем
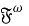
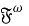
В теореме 1 установим критерий ω регулярности подгруппового m -функтора. Предварительно докажем следующую лемму.
Лемма 1.
Если
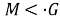
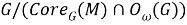
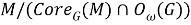
Доказательство.
Пусть
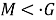
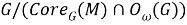
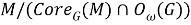
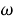
Введем следующие обозначения:
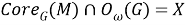


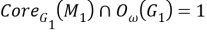
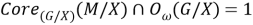
Пусть

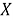

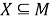
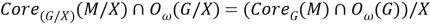
Тогда равенство (2) примет вид:
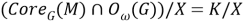
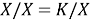
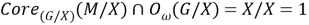
Поскольку
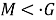
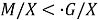
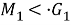
группа
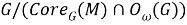
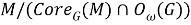
Теорема 1.
Пусть
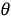
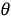
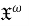
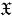
Доказательство.
I. Достаточность. Пусть
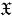
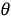
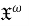
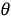
Так как
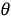
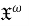
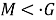
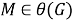
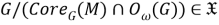
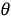
II. Необходимость. Пусть
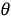
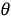
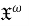
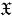
Пусть
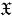
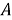
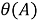
Пусть
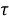
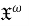
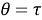

1) Установим, что
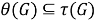
Пусть
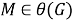
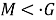
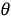
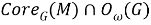

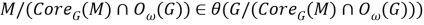
причем, ввиду леммы 1,
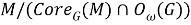
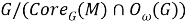
Из (а) и (б), с учетом (*), имеем, что
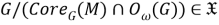
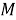
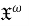

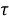
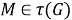
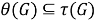
2) Установим, что
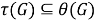
Пусть
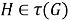
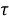
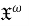
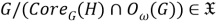
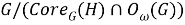
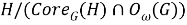
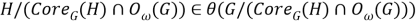
Поскольку
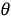
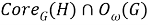

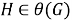
Из (3) и (4) следует, что
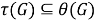
Из 1) и 2) заключаем, что
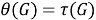
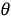
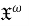
Следуя [2], множество всех
ω
регулярных подгрупповых
m
-функторов обозначим через
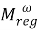

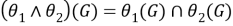
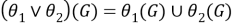
Следуя [2], множество всех
ω
примитивных классов групп обозначим через
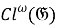
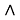
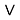
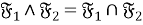
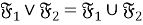
В теореме 2 установлена взаимосвязь решетки
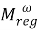
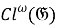
Теорема 2.
Решетки
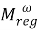
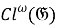
Доказательство.
I. Пусть
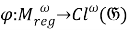
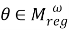
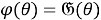
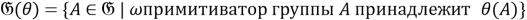
Покажем, что отображение
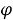
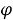
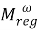
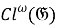
1) Установим, что отображение
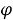
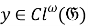
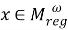
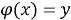
Пусть
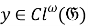
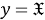
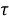

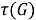

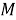
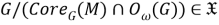
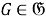
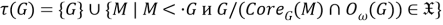
Тогда, в силу теоремы 1 (1) [4, с. 11], отображение
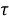
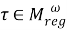
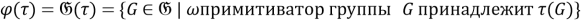
(***). Покажем, что
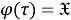
а) Установим, что
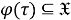
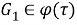
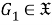
Так как
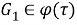
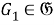
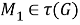
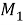
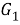
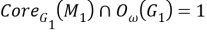
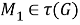
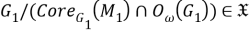
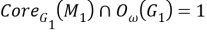
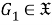
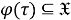
б) Установим, что
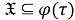
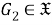
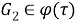
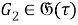
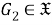
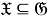
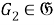
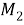
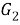
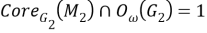
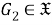
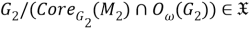
Тогда
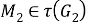
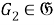
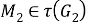
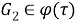
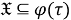
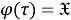
Таким образом, для любого
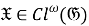
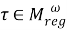
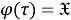
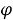
2) Покажем, что отображение
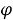
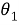

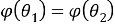
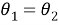
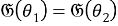
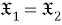
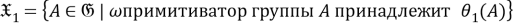
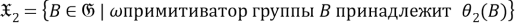
Пусть
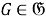
а) Покажем, что
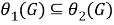
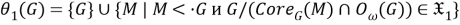
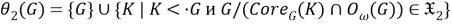
Пусть
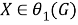
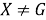
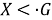
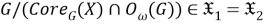
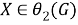
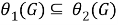
б) Покажем, что
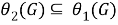
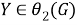
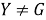
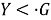
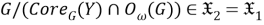
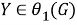
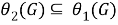
Из а) и б) заключаем, что
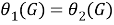
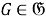
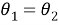
Таким образом, из того, что
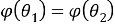
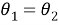
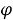
Из 1) и 2) получаем, что отображение
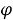
II. Покажем, что отображение
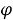
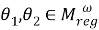
1) Установим, что
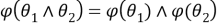
Так как для любой группы

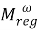
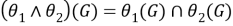
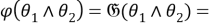
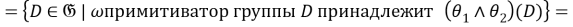
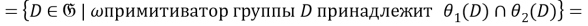
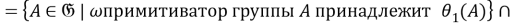
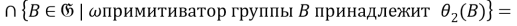
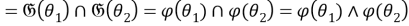
Таким образом,
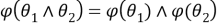
2) Установим, что
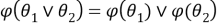
Так как для любой группы

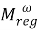
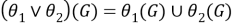
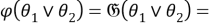
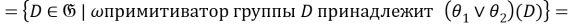
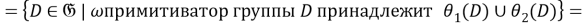
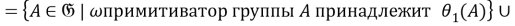
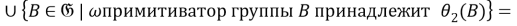
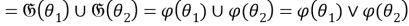
Таким образом,
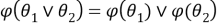
Из 1) и 2) следует, что отображение
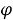
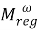
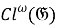
Таким образом, из I и II заключаем, что решетки
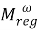
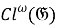
Литература:
-
Ведерников В. А., Сорокина М. М.
- Каморников С. Ф. Обобщенные подгруппы Фраттини как корадикалы групп // Математические заметки. – 2010. – Т. 87, № 3. – С. 402–411.
- Каморников С. Ф., Селькин М. В. Подгрупповые функторы и классы конечных групп. – Минск: Беларуская навука. – 2003. – 254 с.
-
Макаров Д. А. О свойствах
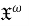
m -функтора // Наука России – будущее страны: сборник статей Всероссийской научно-практической конференции. – Пенза: МЦНС «Наука и Просвещение». – 2022. – С. 10–14. - Монахов В. С. Введение в теорию конечных групп и их классов. – Минск: Вышэйшая школа. – 2006. – 207 с.
- Селькин М. В., Бородич Р. В. О пересечении максимальных подгрупп конечных групп // Вестн. СамГУ. Естественнонаучн. сер. – 2009. – Т. 74, № 8. – С. 67–77.
-
Сорокина М. М., Максаков С. П. О нормальности