В большом количестве прикладных задач, связанных с потребностью в оптимизации каких-либо ресурсов, есть возможность отображения начальных условий на граф. Вершины графа выступают в качестве обозначений контрольных пунктов или ключевых ресурсов, а рёбра графа могут подразумевать под собой не только расстояние, но и время, стоимость или объёмы ресурсов. Это делает графы универсальным инструментом для представления начальных условий в виде, который будет легко обрабатываться вычислительной машиной.
В таком случае появляется потребность в алгоритмах, которые смогут быстро получать оптимальный путь между двумя вершинами графа. Такой путь будет являться решением изначальной задачи. Алгоритмы, связанные с поиском оптимального пути между вершинами графа, названы алгоритмами поиска кратчайшего пути.
Путь в графе — это последовательность смежных вершин.
Кратчайший путь — это путь, который в результате вычисления его рёбер весовой функцией покажет наименьшее значение. Например, если все рёбра графа будут иметь единичный вес, то кратчайший путь — это наименьшее значение весовой функции.
В связи с изменчивостью постановки задачи, существует множество алгоритмов, каждый из которых создан для эффективного нахождения пути в определённых условиях. В этой статье мы рассмотрим три алгоритма, которые применяются особенно часто в решениях задач.
Алгоритм Breadth - First - Search (поиск в ширину):
Это один из методов полного обхода графа, путём последовательного перебора всех вершин. Сначала в очередь для проверки добавляется начальная вершина, а затем все смежные к ней. Далее при проверке каждой вершины, процесс добавления в очередь новых смежных вершин продолжается. То есть, перед переходом к проверке вершин на расстоянии k+1 от начала, сначала проверяются все вершины на уровне k.
Если представить работу алгоритма на графе, подобном по структуре дереву (см. рис. 1), то получим следующее:
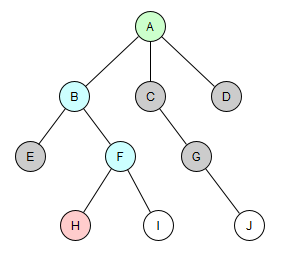
Рис. 1. Работа алгоритма «Поиск в ширину»
- Добавление в очередь на проверку вершины A.
- Проверка A и добавление в очередь вершин B, C и D.
- Проверка B и добавление вершин E и F в конец очереди.
- Проверка C и добавление в очередь G.
- Проверка вершины D.
- Проверка вершины E.
- Проверка вершины F и добавление в очередь H и I.
- Проверка G и добавление в очередь вершины J.
- Проверка H и остановка алгоритма в случае наличия условия на остановку. Получили кратчайший путь: A -> B -> F -> H.
Главное преимущество этого алгоритма — это волновой обход всего графа, что помогает равномерно искать множество целей или одну цель, положение которой неизвестно. В то же время алгоритм не учитывает стоимость перехода от одной вершины к другой, поэтому он подойдёт для тех графов, рёбра которых не имеют веса.
Алгоритм поиска в ширину с прерыванием в случае нахождения конечной вершины на языке программирования Python:

Восстановление конечного пути:

Алгоритм Дейкстры:
Особенность этого алгоритма состоит в том, что, в отличие от «поиска в ширину», алгоритм Дейкстры учитывает «стоимость» перехода от одной вершины к другой, то есть каждое ребро графа получает свою цену. В качестве примера можно привести поиск кратчайшего дорожного пути с учётом автомобильного трафика.
Для учёта стоимости перехода от одной вершины к другой нужно модифицировать алгоритм поиска в ширину, добавив словарь для подсчёта стоимости пути к каждой из обнаруженных вершин, а также приоритетную очередь. С помощью приоритетной очереди алгоритм будет рассматривать самые выгодные маршруты в первую очередь, что позволит ему обходить «дорогостоящие» пути.
Рассмотрим работу алгоритма Дейкстры на графе (см. рис. 2):
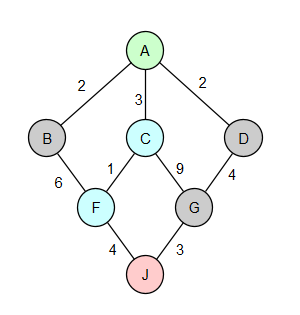
Рис. 2. Работа алгоритма Дейкстры
Приоритет очереди = цена. Чем меньше приоритет, тем выше вершина в очереди.
1) Добавление вершины A в очередь на проверку с ценой 0.
2) Проверка A и добавление в очередь вершин B (цена 2), C (цена 3) и D (цена 2).
3) Из очереди выбирается вершина с наименьшей стоимостью пути. B стоит в очереди выше, чем D, поэтому проверяется вершина B. В очередь добавляется вершина F с общей ценой пути 8.
4) Далее в приоритете на проверку стоит вершина D. Проверка D, в очередь добавляется вершина G с общей ценой пути 6.
5) Проверка вершины С, в очередь добавляются вершины F и G с общими ценами 4 и 12 соответственно.
6) В текущей очереди находятся вершины F (цена 8), G (цена 6), F (цена 4) и G (цена 12). По правилу приоритетной очереди проверяется вершина F. В очередь добавляется вершина J с общей ценой 8.
7) Проверяется вершина G c ценой 6. В очередь добавляется ещё один путь до вершины J с общей ценой 9.
8) Проверка J с ценой 8 и остановка алгоритма в случае наличия условия на остановку. Получили кратчайший путь: A -> C -> F -> J.
Алгоритм Дейкстры с прерыванием в случае нахождения конечной вершины на языке программирования Python:

Восстановление конечного пути:

Минус алгоритма Дейкстры в том, что он тратит лишние ресурсы на проверку вершин, которые могут быть далеко от заранее известной цели и проверка которых нецелесообразна. Эту проблему решает следующий алгоритм.
Алгоритм A * (А звезда):
Этот алгоритм является модифицированной версией алгоритма Дейкстры. Помимо оценки пути с точки зрения стоимости переходов между вершинами, алгоритм A* учитывает положение цели, о которой известно заранее.
С практической точки зрения мы часто сталкиваемся с ситуацией, когда нам известно местоположение цели, поэтому алгоритм «А звезда» может оказаться эффективнее предыдущих двух, описанных выше.
Рассмотрим работу алгоритма «А звезда» на графе (см. рис. 3):
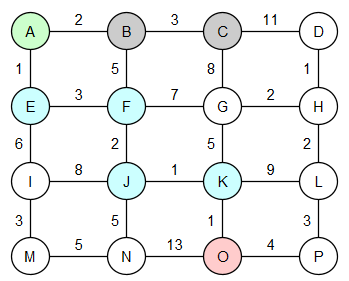
Рис. 3. Работа алгоритма «А звезда»
Приоритет очереди = цена + удалённость от цели. Чем меньше приоритет, тем выше вершина в очереди.
Удалённость от цели = |X текущей вершины — X цели| + |Y текущей вершины — Y цели|.
Координата цели (вершина O): (2, -3).
1) Проверка A (приоритет 0). Добавление в очередь вершин B (цена 2, удалённость 4, приоритет 6) и E (цена 1, удалённость 4, приоритет 5). Текущая очередь: E(5), B(6).
2) Проверка E (приоритет 5, получена из A). Добавление в очередь вершин F (цена 4, удалённость 3, приоритет 7) и I (цена 7, удалённость 3, приоритет 10). Текущая очередь: B(6), F(7), I(10).
3) Проверка B (приоритет 6, получена из A). Добавление в очередь вершин C (цена 5, удалённость 3, приоритет 8) и F (цена 7, удалённость 3, приоритет 10). Текущая очередь: F(7), C(8), I(10), F(10).
4) Проверка F (приоритет 7, получена из E). Добавление в очередь G (цена 11, удалённость 2, приоритет 13) и J (цена 6, удалённость 2, приоритет 8). Текущая очередь: C(8), J(8), I(10), F(10), G(13).
5) Проверка C (приоритет 8, получена из B). Добавление в очередь G (цена 13, удалённость 2, приоритет 15) и D (цена 16, удалённость 4, приоритет 20). Текущая очередь: J(8), I(10), F(10), G(14), G(15), D(20).
6) Проверка J (приоритет 8, получена из F). Добавление в очередь K (цена 7, удалённость 1, приоритет 8) и N (цена 11, удалённость 1, приоритет 12). Текущая очередь: K(8), I(10), F(10), N(12), G(14), G(15), D(20).
7) Проверка K (приоритет 8, получена из J). Добавление в очередь L (цена 16, удалённость 2, приоритет 18) и O (цена 8, удалённость 0, приоритет 8). Текущая очередь: O(8), I(10), F(10), N(12), G(14), G(15), L(18), D(20).
8) Проверка вершины O (приоритет 8, получена из K). Остановка алгоритма в случае наличия условия на остановку. Получили кратчайший путь: A -> E -> F -> J -> K -> O.
Функция, описывающая близость текущего местоположения и конечного (используется далее в коде алгоритма):

Алгоритм A* с прерыванием в случае нахождения конечной вершины на языке программирования Python:

Восстановление конечного пути:

Итог к разбору алгоритмов.
Три этих алгоритма являются одними из наиболее часто применяемых способов нахождения оптимального пути в практических ситуациях. Конечно, алгоритм «А звезда» выделяется среди них особенно. Вбирая в себя технику алгоритма Дейкстры и, при этом, учитывая расстояние до известной цели, он позволяет быстро и точно находить кратчайший путь в чётко заданных условиях. Тем не менее, алгоритм «Поиск в ширину» и алгоритм Дейкстры также находят своё применение.
Алгоритм «Поиск в ширину» не только закладывает основной метод перебора вершин графа, но и сам по себе имеет практическое значение. Этим алгоритмом очень удобно находить одну или несколько целей, положение которых неизвестно заранее, в ситуациях, когда вес рёбер графа не имеет значения. Алгоритм Дейкстры схож в применении с алгоритмом «Поиска в ширину», при этом позволяет оценивать стоимость переходов между вершинами графа.
Алгоритмы нахождения кратчайшего пути являются важной частью дискретной математики и компьютерных наук в целом. Они позволяют находить путь не только в прямом понимании (кратчайший путь на картах внутри смартфонов и GPS-навигаторов), но и в значении наиболее выгодного пути, как это происходит в экономических задачах.
Визуализация на базе движка Unity
В качестве дополнения к подробному разбору алгоритмов нахождения кратчайшего пути приводим способ реализации одного из них на базе движка Unity. Реализация алгоритма на базе движка позволит автоматически перемещать игровые объекты на сцене от начальной позиции к конечной, учитывая наличие препятствий.
Визуализация алгоритма «Поиск в ширину» в сцене движка Unity:
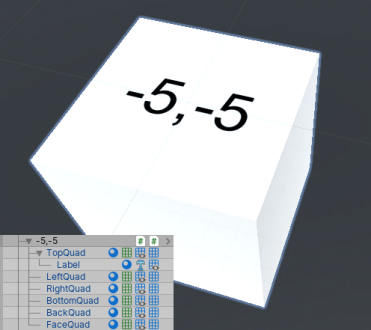
Рис. 4. Куб, выступающий в роли вершины
- В качестве вершин у нас будут выступать кубы, составленные из четырёхугольников. «Label» на верхнем четырёхугольнике будет хранить в себе компонент Text Mesh для вывода положения вершины в пространстве (см. рис. 4). Mesh Renderer верхнего четырёхугольника будет окрашиваться в цвета, показывая его состояние в результате работы алгоритма.
- К каждому кубу будет прикреплён скрипт Waypoint, который может возвращать положение куба в сетке, а также хранить его состояние в ходе работы алгоритма. Waypoint.cs:

- Все кубы-вершины находятся внутри пустого объекта «Grid». Этот объект принимает скрипт Pathfinder, в котором заключается алгоритм нахождения кратчайшего пути «Поиск в ширину». Pathfinder.cs:

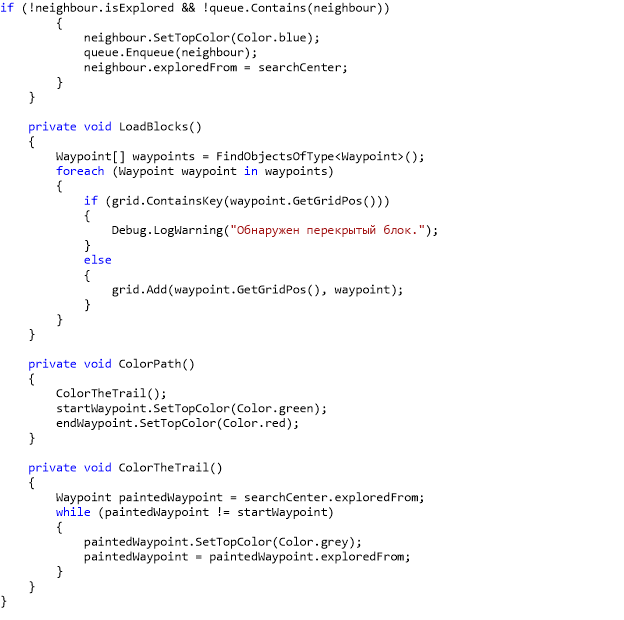
- Дублируем кубы-вершины, расставляем их в виде сетки и выбираем в полях скрипта Pathfinder начальную и конечную вершину. После запуска сцены видим визуальное отображение работы алгоритма.








